Formler för exponentiella ekvationer. Vad är en exponentiell ekvation och hur man löser den
Exempel:
\(4^x=32\)
\(5^(2x-1)-5^(2x-3)=4,8\)
\((\sqrt(7))^(2x+2)-50\cdot(\sqrt(7))^(x)+7=0\)
Hur man löser exponentiella ekvationer
När vi löser en exponentiell ekvation strävar vi efter att få den till formen \(a ^ (f (x)) \u003d a ^ (g (x)) \), och sedan göra övergången till indikatorernas likhet, det vill säga:
\(a^(f(x))=a^(g(x))\) \(⇔\) \(f(x)=g(x)\)
Till exempel:\(2^(x+1)=2^2\) \(⇔\) \(x+1=2\)
Viktig! Från samma logik följer två krav för en sådan övergång:
- nummer in vänster och höger ska vara samma;
- grader vänster och höger måste vara "rena", det vill säga det ska inte finnas några, multiplikationer, divisioner osv.
Till exempel:
För att få ekvationen till formen \(a^(f(x))=a^(g(x))\) och används.
Exempel
. Lös exponentialekvationen \(\sqrt(27) 3^(x-1)=((\frac(1)(3)))^(2x)\)
Lösning:
|
\(\sqrt(27) 3^(x-1)=((\frac(1)(3)))^(2x)\) |
Vi vet att \(27 = 3^3\). Med detta i åtanke omvandlar vi ekvationen. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(\sqrt(3^3) 3^(x-1)=((\frac(1)(3)))^(2x)\) |
Genom egenskapen för roten \(\sqrt[n](a)=a^(\frac(1)(n))\) får vi att \(\sqrt(3^3)=((3^3) )^( \frac(1)(2))\). Vidare, med hjälp av gradens egenskap \((a^b)^c=a^(bc)\), får vi \(((3^3))^(\frac(1)(2))=3^( 3 \ cdot \frac(1)(2))=3^(\frac(3)(2))\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(\frac(3)(2))\cdot 3^(x-1)=(\frac(1)(3))^(2x)\) |
Vi vet också att \(a^b a^c=a^(b+c)\). Om vi applicerar detta på vänster sida får vi: \(3^(\frac(3)(2)) 3^(x-1)=3^(\frac(3)(2)+ x-1)=3 ^ (1,5 + x-1)=3^(x+0,5)\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(x+0,5)=(\frac(1)(3))^(2x)\) |
Kom nu ihåg att: \(a^(-n)=\frac(1)(a^n)\). Denna formel kan också användas i baksidan: \(\frac(1)(a^n) =a^(-n)\). Sedan \(\frac(1)(3)=\frac(1)(3^1) =3^(-1)\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(x+0,5)=(3^(-1))^(2x)\) |
Genom att applicera egenskapen \((a^b)^c=a^(bc)\) på höger sida får vi: \((3^(-1))^(2x)=3^((-1) 2x) =3^(-2x)\). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(3^(x+0,5)=3^(-2x)\) |
Och nu har vi baserna lika och det finns inga störande koefficienter osv. Så vi kan göra omställningen. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exempel
. Lös exponentialekvationen \(4^(x+0,5)-5 2^x+2=0\)
Svar : \(-1; 1\). Frågan kvarstår - hur ska man förstå när man ska tillämpa vilken metod? Det kommer med erfarenhet. Under tiden har du inte förtjänat det, använd allmän rekommendation att lösa komplexa problem - "om du inte vet vad du ska göra - gör vad du kan." Det vill säga leta efter hur du i princip kan transformera ekvationen, och försök göra det - tänk om den kommer ut? Huvudsaken är att endast göra matematiskt motiverade transformationer. exponentiella ekvationer utan lösningarLåt oss titta på ytterligare två situationer som ofta förbryllar eleverna: Låt oss försöka lösa det med brutalt våld. Om x är ett positivt tal, kommer hela potensen \(2^x\) att växa när x växer: \(x=1\); \(2^1=2\) \(x=0\); \(2^0=1\) Även tidigare. Det finns negativa x. När vi kommer ihåg egenskapen \(a^(-n)=\frac(1)(a^n)\), kontrollerar vi: \(x=-1\); \(2^(-1)=\frac(1)(2^1)=\frac(1)(2)\) Trots att antalet blir mindre för varje steg kommer det aldrig att nå noll. Så den negativa graden räddade inte oss heller. Vi kommer till en logisk slutsats: Ett positivt tal till valfri potens förblir ett positivt tal.Båda ekvationerna ovan har alltså inga lösningar. exponentiella ekvationer med olika baserI praktiken finns det ibland exponentiella ekvationer med olika baser som inte är reducerbara till varandra, och samtidigt med samma exponenter. De ser ut så här: \(a^(f(x))=b^(f(x))\), där \(a\) och \(b\) är positiva tal. Till exempel: \(7^(x)=11^(x)\) Sådana ekvationer kan enkelt lösas genom att dividera med någon av ekvationens delar (vanligtvis dividera med höger sida, det vill säga med \ (b ^ (f (x)) \). Du kan dividera på detta sätt, eftersom en positiv talet är positivt i någon grad (det vill säga vi dividerar inte med noll.) Vi får: \(\frac(a^(f(x)))(b^(f(x)))\) \(=1\) Exempel
. Lös exponentialekvationen \(5^(x+7)=3^(x+7)\)
Svar : \(-7\). Ibland är "likheten" hos exponenterna inte uppenbar, men den skickliga användningen av gradens egenskaper löser denna fråga. Exempel
. Lös exponentialekvationen \(7^( 2x-4)=(\frac(1)(3))^(-x+2)\)
Svar : \(2\). |
I förberedelsestadiet för det slutliga testet måste gymnasieelever förbättra sina kunskaper om ämnet "Exponentiella ekvationer". De senaste årens erfarenheter tyder på att sådana uppgifter medför vissa svårigheter för skolbarn. Därför måste gymnasieelever, oavsett deras förberedelsenivå, noggrant bemästra teorin, memorera formlerna och förstå principen för att lösa sådana ekvationer. Efter att ha lärt sig att klara av denna typ av uppgifter kommer akademiker att kunna räkna med höga poäng när de klarar provet i matematik.
Gör dig redo för examensprovningen tillsammans med Shkolkovo!
När man upprepar det material som tas upp, ställs många elever inför problemet att hitta de formler som behövs för att lösa ekvationerna. En skolbok finns inte alltid till hands, och valet av nödvändig information om ett ämne på Internet tar lång tid.
Shkolkovo utbildningsportal inbjuder studenter att använda vår kunskapsbas. Vi implementerar helt ny metod förberedelse för det sista provet. Genom att studera på vår webbplats kommer du att kunna identifiera luckor i kunskap och uppmärksamma just de uppgifter som orsakar de största svårigheterna.
Lärarna i "Shkolkovo" samlade, systematiserade och presenterade allt som behövs för en framgångsrik klara provet material i den mest enkla och lättillgängliga formen.
De viktigaste definitionerna och formlerna presenteras i avsnittet "Teoretisk referens".
För en bättre assimilering av materialet rekommenderar vi att du övar på uppgifterna. Ta en titt på exemplen på den här sidan. exponentiella ekvationer med en lösning för att förstå beräkningsalgoritmen. Fortsätt sedan med uppgifterna i avsnittet "Kataloger". Du kan börja med de enklaste uppgifterna eller gå direkt till att lösa komplexa exponentialekvationer med flera okända eller . Databasen med övningar på vår hemsida kompletteras och uppdateras ständigt.
De exemplen med indikatorer som orsakade dig svårigheter kan läggas till i "Favoriter". Så du kan snabbt hitta dem och diskutera lösningen med läraren.
För att klara provet, studera på Shkolkovo-portalen varje dag!
Den här lektionen är avsedd för dem som precis har börjat lära sig exponentiella ekvationer. Som alltid, låt oss börja med en definition och enkla exempel.
Om du läser den här lektionen, så misstänker jag att du redan har åtminstone en minimal förståelse för de enklaste ekvationerna - linjära och kvadratiska: $56x-11=0$; $((x)^(2))+5x+4=0$; $((x)^(2))-12x+32=0$ osv. Att kunna lösa sådana konstruktioner är absolut nödvändigt för att inte "hänga" i ämnet som kommer att diskuteras nu.
Exponentiella ekvationer alltså. Låt mig ge dig ett par exempel:
\[((2)^(x))=4;\quad ((5)^(2x-3))=\frac(1)(25);\quad ((9)^(x))=- 3\]
Vissa av dem kan verka mer komplicerade för dig, vissa av dem är tvärtom för enkla. Men alla förenas av en viktig egenskap: de innehåller en exponentiell funktion $f\left(x \right)=((a)^(x))$. Därför introducerar vi definitionen:
En exponentiell ekvation är vilken ekvation som helst som innehåller en exponentialfunktion, dvs. ett uttryck av formen $((a)^(x))$. Förutom den specificerade funktionen kan sådana ekvationer innehålla andra algebraiska konstruktioner - polynom, rötter, trigonometri, logaritmer, etc.
Okej då. Förstod definitionen. Nu är frågan: hur löser man allt detta skit? Svaret är både enkelt och komplext på samma gång.
Låt oss börja med de goda nyheterna: från min erfarenhet med många elever kan jag säga att för de flesta av dem är exponentiella ekvationer mycket lättare än samma logaritmer, och ännu mer trigonometri.
Men det finns också dåliga nyheter: ibland får problemkompilatorerna för alla typer av läroböcker och tentor besök av "inspiration", och deras droginflammerade hjärna börjar producera så brutala ekvationer att det blir problematiskt inte bara för eleverna att lösa dem - även många lärare fastnar på sådana problem.
Men låt oss inte prata om sorgliga saker. Och låt oss återgå till de tre ekvationerna som gavs i början av berättelsen. Låt oss försöka lösa var och en av dem.
Första ekvationen: $((2)^(x))=4$. Tja, till vilken makt måste siffran 2 höjas för att få siffran 4? Kanske den andra? När allt kommer omkring är $((2)^(2))=2\cdot 2=4$ — och vi har fått den korrekta numeriska likheten, d.v.s. faktiskt $x=2$. Tja, tack, mössa, men den här ekvationen var så enkel att även min katt kunde lösa den. :)
Låt oss titta på följande ekvation:
\[((5)^(2x-3))=\frac(1)(25)\]
Men här är det lite svårare. Många elever vet att $((5)^(2))=25$ är multiplikationstabellen. Vissa misstänker också att $((5)^(-1))=\frac(1)(5)$ i huvudsak är definitionen av negativa exponenter (liknande formeln $((a)^(-n))= \ frac(1)(((a)^(n)))$).
Slutligen, bara ett fåtal utvalda gissar att dessa fakta kan kombineras och resultatet är följande resultat:
\[\frac(1)(25)=\frac(1)(((5)^(2)))=((5)^(-2)))\]
Således kommer vår ursprungliga ekvation att skrivas om enligt följande:
\[((5)^(2x-3))=\frac(1)(25)\Högerpil ((5)^(2x-3))=((5)^(-2))\]
Och nu är detta redan helt löst! På vänster sida av ekvationen finns en exponentialfunktion, på höger sida av ekvationen finns en exponentialfunktion, det finns inget annat än dem någon annanstans. Därför är det möjligt att "kassera" baserna och dumt likställa indikatorerna:
Vi har den enklaste linjära ekvationen som alla elever kan lösa på bara ett par rader. Okej, på fyra rader:
\[\begin(align)& 2x-3=-2 \\& 2x=3-2 \\& 2x=1 \\& x=\frac(1)(2) \\\end(align)\]
Om du inte förstår vad som hände på de senaste fyra raderna, se till att gå tillbaka till ämnet "linjära ekvationer" och upprepa det. För utan en tydlig assimilering av detta ämne är det för tidigt för dig att ta dig an exponentiella ekvationer.
\[((9)^(x))=-3\]
Tja, hur bestämmer du dig? Första tanke: $9=3\cdot 3=((3)^(2))$, så den ursprungliga ekvationen kan skrivas om så här:
\[((\vänster(((3)^(2)) \höger))^(x))=-3\]
Sedan kommer vi ihåg att när man höjer en grad till en makt, multipliceras indikatorerna:
\[((\vänster(((3)^(2)) \höger))^(x))=((3)^(2x))\Högerpil ((3)^(2x))=-(( 3)^(1))\]
\[\begin(align)& 2x=-1 \\& x=-\frac(1)(2) \\\end(align)\]
Och för ett sådant beslut får vi en ärligt välförtjänt tvåa. För vi, med en Pokémons jämnmod, skickade minustecknet framför de tre till kraften av just dessa tre. Och det kan du inte göra. Och det är varför. Ta en titt på trippelns olika krafter:
\[\begin(matris) ((3)^(1))=3& ((3)^(-1))=\frac(1)(3)& ((3)^(\frac(1)( 2)))=\sqrt(3) \\ ((3)^(2))=9& ((3)^(-2))=\frac(1)(9)& ((3)^(\ frac(1)(3)))=\sqrt(3) \\ ((3)^(3))=27& ((3)^(-3))=\frac(1)(27)& (( 3)^(-\frac(1)(2)))=\frac(1)(\sqrt(3)) \\\end(matris)\]
När jag kompilerade den här surfplattan perverterade jag inte så snart som möjligt: jag övervägde positiva grader, och negativa, och till och med bråkdelar ... ja, var är åtminstone en ett negativt tal? Han är inte! Och det kan det inte vara, eftersom exponentialfunktionen $y=((a)^(x))$ för det första alltid bara tar positiva värden(oavsett hur mycket du multiplicerar en eller dividerar med två, kommer det fortfarande att vara ett positivt tal), och för det andra är basen för en sådan funktion - talet $a$ - per definition ett positivt tal!
Tja, hur löser man då ekvationen $((9)^(x))=-3$? Nej, det finns inga rötter. Och i den meningen är exponentiella ekvationer väldigt lika andragradsekvationer - det kan inte heller finnas några rötter. Men om antalet rötter i andragradsekvationer bestäms av diskriminanten (diskriminanten är positiv - 2 rötter, negativ - inga rötter), så beror det i exponentiella ekvationer på vad som står till höger om likhetstecknet.
Således formulerar vi nyckelslutsatsen: den enklaste exponentiella ekvationen av formen $((a)^(x))=b$ har en rot om och endast om $b>0$. Genom att känna till detta enkla faktum kan du enkelt avgöra om ekvationen som föreslagits för dig har rötter eller inte. De där. är det värt att lösa det överhuvudtaget eller omedelbart skriva ner att det inte finns några rötter.
Denna kunskap kommer att hjälpa oss många gånger om när vi ska lösa mer komplexa problem. Under tiden, tillräckligt med texter - det är dags att studera den grundläggande algoritmen för att lösa exponentiella ekvationer.
Hur man löser exponentiella ekvationer
Så låt oss formulera problemet. Det är nödvändigt att lösa exponentialekvationen:
\[((a)^(x))=b,\quad a,b>0\]
Enligt den "naiva" algoritmen som vi använde tidigare är det nödvändigt att representera talet $b$ som en potens av talet $a$:
Dessutom, om det istället för variabeln $x$ finns något uttryck, får vi en ny ekvation, som redan kan lösas. Till exempel:
\[\begin(align)& ((2)^(x))=8\Högerpil ((2)^(x))=((2)^(3))\Högerpil x=3; \\& ((3)^(-x))=81\Högerpil ((3)^(-x))=((3)^(4))\Högerpil -x=4\Högerpil x=-4; \\& ((5)^(2x))=125\Högerpil ((5)^(2x))=((5)^(3))\Högerpil 2x=3\Högerpil x=\frac(3)( 2). \\\end(align)\]
Och konstigt nog fungerar detta system i cirka 90% av fallen. Hur är det med de övriga 10% då? De återstående 10% är lätt "schizofrena" exponentiella ekvationer av formen:
\[((2)^(x))=3;\quad ((5)^(x))=15;\quad ((4)^(2x))=11\]
Till vilken makt behöver du höja 2 för att få 3? I den första? Men nej: $((2)^(1))=2$ räcker inte. På sekunden? Varken: $((2)^(2))=4$ är för mycket. Vad händer då?
Kunniga studenter har förmodligen redan gissat: i sådana fall, när det är omöjligt att lösa "vackert", är "tungt artilleri" kopplat till fallet - logaritmer. Låt mig påminna dig om att med logaritmer kan vilket positivt tal som helst representeras som en potens av vilket annat positivt tal som helst (med undantag av ett):
Kommer du ihåg den här formeln? När jag berättar för mina elever om logaritmer, varnar jag er alltid: den här formeln (det är också den grundläggande logaritmiska identiteten eller, om du så vill, definitionen av logaritmen) kommer att förfölja dig under mycket lång tid och "uppstå" i de flesta oväntade platser. Nåväl, hon dök upp. Låt oss titta på vår ekvation och denna formel:
\[\begin(align)& ((2)^(x))=3 \\& a=((b)^(((\log )_(b))a)) \\\end(align) \]
Om vi antar att $a=3$ är vårt ursprungliga nummer till höger och $b=2$ är själva basen exponentiell funktion, som vi så gärna vill reducera den högra sidan till, får vi följande:
\[\begin(align)& a=((b)^(((\log )_(b))a))\Högerpil 3=((2)^(((\log )_(2))3 )); \\& ((2)^(x))=3\Högerpil ((2)^(x))=((2)^(((\log )_(2))3))\Högerpil x=( (\log )_(2))3. \\\end(align)\]
Vi fick ett lite konstigt svar: $x=((\log )_(2))3$. I någon annan uppgift, med ett sådant svar, skulle många tvivla och börja dubbelkolla sin lösning: tänk om det var ett misstag någonstans? Jag skyndar mig att behaga dig: det finns inget fel här, och logaritmer i rötterna till exponentiella ekvationer är en ganska typisk situation. Så vänja dig. :)
Nu löser vi analogt de återstående två ekvationerna:
\[\begin(align)& ((5)^(x))=15\Högerpil ((5)^(x))=((5)^(((\log )_(5))15)) \Högerpil x=((\log )_(5))15; \\& ((4)^(2x))=11\Högerpil ((4)^(2x))=((4)^(((\log )_(4))11))\Högerpil 2x=( (\log )_(4))11\Högerpil x=\frac(1)(2)((\log )_(4))11. \\\end(align)\]
Det är allt! Förresten, det sista svaret kan skrivas annorlunda:
Det var vi som introducerade multiplikatorn i logaritmens argument. Men ingen hindrar oss från att lägga till denna faktor till basen:
I det här fallet är alla tre alternativen korrekta - det är bara olika former poster med samma nummer. Vilken du ska välja och skriva ner i detta beslut är upp till dig.
Vi har alltså lärt oss att lösa alla exponentiella ekvationer av formen $((a)^(x))=b$, där talen $a$ och $b$ är strikt positiva. Men den hårda verkligheten i vår värld är att sådana enkla uppgifter kommer att möta dig mycket, mycket sällan. Oftare kommer du att stöta på något i stil med detta:
\[\begin(align)& ((4)^(x))+((4)^(x-1))=((4)^(x+1))-11; \\& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2,7)^(1-x))=0,09. \\\end(align)\]
Tja, hur bestämmer du dig? Kan detta överhuvudtaget lösas? Och i så fall hur?
Ingen panik. Alla dessa ekvationer reduceras snabbt och enkelt till de enkla formler som vi redan har övervägt. Du behöver bara veta för att komma ihåg ett par knep från algebrakursen. Och självklart finns det inga regler för att arbeta med examina här. Jag ska prata om allt det här nu. :)
Transformation av exponentiella ekvationer
Det första att komma ihåg är att varje exponentiell ekvation, oavsett hur komplex den kan vara, på ett eller annat sätt måste reduceras till de enklaste ekvationerna - just de som vi redan har övervägt och som vi vet hur vi ska lösa. Med andra ord, schemat för att lösa alla exponentiella ekvationer ser ut så här:
- Skriv ner den ursprungliga ekvationen. Till exempel: $((4)^(x))+((4)^(x-1))=((4)^(x+1))-11$;
- Gör lite dumt skit. Eller till och med något skit som heter "förvandla ekvationen";
- Vid utgången får du de enklaste uttrycken som $((4)^(x))=4$ eller något annat liknande. Dessutom kan en initial ekvation ge flera sådana uttryck samtidigt.
Med den första punkten är allt klart - även min katt kan skriva ekvationen på ett löv. Även med den tredje punkten verkar det vara mer eller mindre klart - vi har redan löst en hel massa sådana ekvationer ovan.
Men hur är det med den andra punkten? Vilka är förvandlingarna? Vad ska man konvertera till vad? Och hur?
Nåväl, låt oss ta reda på det. Först och främst vill jag påpeka följande. Alla exponentialekvationer är indelade i två typer:
- Ekvationen är sammansatt av exponentialfunktioner med samma bas. Exempel: $((4)^(x))+((4)^(x-1))=((4)^(x+1))-11$;
- Formeln innehåller exponentialfunktioner med olika baser. Exempel: $((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x))$ och $((100)^(x-1) )\cdot ((2,7)^(1-x))=0,09$.
Låt oss börja med ekvationer av den första typen - de är lättast att lösa. Och i deras lösning kommer vi att få hjälp av en sådan teknik som valet av stabila uttryck.
Att lyfta fram ett stabilt uttryck
Låt oss titta på denna ekvation igen:
\[((4)^(x))+((4)^(x-1))=((4)^(x+1))-11\]
Vad ser vi? De fyra är upphöjda i olika grad. Men alla dessa potenser är enkla summor av variabeln $x$ med andra tal. Därför är det nödvändigt att komma ihåg reglerna för att arbeta med grader:
\[\begin(align)& ((a)^(x+y))=((a)^(x))\cdot ((a)^(y)); \\& ((a)^(xy))=((a)^(x)):((a)^(y))=\frac(((a)^(x)))(((a) )^(y))). \\\end(align)\]
Enkelt uttryckt kan addition av exponenter omvandlas till en produkt av potenser, och subtraktion omvandlas enkelt till division. Låt oss försöka tillämpa dessa formler på potenserna från vår ekvation:
\[\begin(align)& ((4)^(x-1))=\frac(((4)^(x)))(((4)^(1)))=((4)^ (x))\cdot \frac(1)(4); \\& ((4)^(x+1))=((4)^(x))\cdot ((4)^(1))=((4)^(x))\cdot 4. \ \\end(align)\]
Vi skriver om den ursprungliga ekvationen med hänsyn till detta faktum, och sedan samlar vi alla termer till vänster:
\[\begin(align)& ((4)^(x))+(4)^(x))\cdot \frac(1)(4)=((4)^(x))\cdot 4 -elva; \\& ((4)^(x))+((4)^(x))\cdot \frac(1)(4)-((4)^(x))\cdot 4+11=0. \\\end(align)\]
I fyra första termer, det finns ett element $((4)^(x))$ — vi tar det ur parentesen:
\[\begin(align)& ((4)^(x))\cdot \left(1+\frac(1)(4)-4 \right)+11=0; \\& ((4)^(x))\cdot \frac(4+1-16)(4)+11=0; \\& ((4)^(x))\cdot \left(-\frac(11)(4) \right)=-11. \\\end(align)\]
Det återstår att dividera båda delarna av ekvationen med bråket $-\frac(11)(4)$, d.v.s. multiplicera i huvudsak med det inverterade bråket - $-\frac(4)(11)$. Vi får:
\[\begin(align)& ((4)^(x))\cdot \left(-\frac(11)(4) \right)\cdot \left(-\frac(4)(11) \right )=-11\cdot \left(-\frac(4)(11) \right); \\& ((4)^(x))=4; \\& ((4)^(x))=((4)^(1)); \\&x=1. \\\end(align)\]
Det är allt! Vi reducerade den ursprungliga ekvationen till den enklaste och fick det slutliga svaret.
Samtidigt upptäckte vi (och tog till och med ur parentesen) under processen att lösa den gemensamma faktorn $((4)^(x))$ - detta är det stabila uttrycket. Den kan betecknas som en ny variabel, eller så kan du helt enkelt uttrycka den korrekt och få ett svar. I alla fall, nyckelprincip lösningarna är följande:
Hitta i den ursprungliga ekvationen ett stabilt uttryck som innehåller en variabel som lätt kan särskiljas från alla exponentialfunktioner.
Den goda nyheten är att nästan varje exponentiell ekvation medger ett så stabilt uttryck.
Men det finns också dåliga nyheter: sådana uttryck kan vara väldigt knepiga, och det kan vara ganska svårt att skilja dem åt. Så låt oss titta på ett annat problem:
\[((5)^(x+2))+((0,2)^(-x-1))+4\cdot ((5)^(x+1))=2\]
Kanske kommer någon nu att ha en fråga: "Pasha, är du stenad? Här finns olika baser - 5 och 0,2. Men låt oss försöka konvertera en potens med basen 0,2. Låt oss till exempel bli av med decimalbråket och föra det till det vanliga:
\[((0,2)^(-x-1))=((0,2)^(-\vänster(x+1 \höger)))=((\left(\frac(2)(10) ) \höger))^(-\vänster(x+1 \höger)))=((\vänster(\frac(1)(5) \höger))^(-\vänster(x+1 \höger)) )\]
Som du kan se dök siffran 5 fortfarande upp, om än i nämnaren. Samtidigt skrevs indikatorn om till negativ. Och nu minns vi en av väsentliga regler arbeta med examina:
\[((a)^(-n))=\frac(1)(((a)^(n)))\Högerpil ((\left(\frac(1)(5) \right))^( -\vänster(x+1 \höger)))=((\vänster(\frac(5)(1) \höger))^(x+1))=((5)^(x+1))\ ]
Här fuskade jag såklart lite. För för en fullständig förståelse måste formeln för att bli av med negativa indikatorer skrivas enligt följande:
\[((a)^(-n))=\frac(1)((a)^(n)))=((\left(\frac(1)(a) \right))^(n ))\Högerpil ((\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=((\left(\frac(5)(1) \ höger))^(x+1))=((5)^(x+1))\]
Å andra sidan hindrade ingenting oss från att arbeta med endast en bråkdel:
\[((\left(\frac(1)(5) \right))^(-\left(x+1 \right)))=((\left(((5)^(-1)) \ höger))^(-\left(x+1 \right)))=((5)^(\left(-1 \right)\cdot \left(-\left(x+1 \right) \right) ))=((5)^(x+1))\]
Men i det här fallet måste du kunna höja en grad till en annan grad (jag påminner dig: i det här fallet läggs indikatorerna ihop). Men jag behövde inte "vända" bråken - kanske för någon blir det lättare. :)
I vilket fall som helst kommer den ursprungliga exponentiella ekvationen att skrivas om som:
\[\begin(align)& ((5)^(x+2))+((5)^(x+1))+4\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+5\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(1))\cdot ((5)^(x+1))=2; \\& ((5)^(x+2))+((5)^(x+2))=2; \\& 2\cdot ((5)^(x+2))=2; \\& ((5)^(x+2))=1. \\\end(align)\]
Så det visar sig att den ursprungliga ekvationen är ännu lättare att lösa än den tidigare övervägda: här behöver du inte ens peka ut ett stabilt uttryck - allt har reducerats av sig självt. Det återstår bara att komma ihåg att $1=((5)^(0))$, varifrån vi får:
\[\begin(align)& ((5)^(x+2))=((5)^(0)); \\&x+2=0; \\&x=-2. \\\end(align)\]
Det är hela lösningen! Vi fick det sista svaret: $x=-2$. Samtidigt skulle jag vilja notera ett knep som avsevärt förenklade alla beräkningar för oss:
I exponentiella ekvationer, se till att bli av med decimalbråk konvertera dem till normala. Detta gör att du kan se samma grunder för graderna och avsevärt förenkla lösningen.
Låt oss nu gå vidare till mer komplexa ekvationer där det finns olika baser, som i allmänhet inte kan reduceras till varandra med hjälp av potenser.
Använder exponentegenskapen
Låt mig påminna dig om att vi har ytterligare två särskilt hårda ekvationer:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& ((100)^(x-1))\cdot ((2,7)^(1-x))=0,09. \\\end(align)\]
Den största svårigheten här är att det inte är klart vad och till vilken grund man ska leda. Var finns de fasta uttrycken? Var finns de gemensamma grunderna? Det finns inget av detta.
Men låt oss försöka gå åt andra hållet. Om det inte finns några färdiga identiska baser kan du försöka hitta dem genom att faktorisera de tillgängliga baserna.
Låt oss börja med den första ekvationen:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((21)^(3x)); \\& 21=7\cdot 3\Högerpil ((21)^(3x))=((\left(7\cdot 3 \right))^(3x))=((7)^(3x))\ cdot ((3)^(3x)). \\\end(align)\]
Men du kan göra tvärtom - gör upp siffran 21 från siffrorna 7 och 3. Det är särskilt lätt att göra detta till vänster, eftersom indikatorerna för båda graderna är desamma:
\[\begin(align)& ((7)^(x+6))\cdot ((3)^(x+6))=((\left(7\cdot 3 \right))^(x+ 6 ))=((21)^(x+6)); \\& ((21)^(x+6))=((21)^(3x)); \\&x+6=3x; \\& 2x=6; \\&x=3. \\\end(align)\]
Det är allt! Du tog exponenten ur produkten och fick direkt en vacker ekvation som kan lösas på ett par rader.
Låt oss nu ta itu med den andra ekvationen. Här är allt mycket mer komplicerat:
\[((100)^(x-1))\cdot ((2,7)^(1-x))=0,09\]
\[((100)^(x-1))\cdot ((\left(\frac(27)(10) \right))^(1-x))=\frac(9)(100)\]
I det här fallet visade sig fraktionerna vara irreducerbara, men om något kunde reduceras, se till att minska det. Detta kommer ofta att resultera i intressanta grunder som du redan kan arbeta med.
Tyvärr har vi inte kommit fram till något. Men vi ser att exponenterna till vänster i produkten är motsatta:
Låt mig påminna dig: för att bli av med minustecknet i exponenten behöver du bara "vända" bråket. Så låt oss skriva om den ursprungliga ekvationen:
\[\begin(align)& ((100)^(x-1))\cdot ((\left(\frac(10)(27) \right))^(x-1))=\frac(9) )(ett hundra); \\& ((\left(100\cdot \frac(10)(27) \right))^(x-1))=\frac(9)(100); \\& ((\left(\frac(1000)(27) \right))^(x-1))=\frac(9)(100). \\\end(align)\]
På den andra raden placerade vi bara inom parentes summan från produkten enligt regeln $((a)^(x))\cdot ((b)^(x))=((\left(a\cdot b \right ))^ (x))$, och i den senare multiplicerade de helt enkelt talet 100 med en bråkdel.
Notera nu att siffrorna till vänster (vid basen) och till höger är något liknande. Hur? Ja, uppenbarligen: de är makter av samma nummer! Vi har:
\[\begin(align)& \frac(1000)(27)=\frac(((10)^(3)))(((3)^(3)))=((\left(\frac( 10)(3) \höger))^(3)); \\& \frac(9)(100)=\frac(((3)^(2)))(((10)^(3)))=((\left(\frac(3)(10) \höger))^(2)). \\\end(align)\]
Därför kommer vår ekvation att skrivas om enligt följande:
\[((\left(((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=(\left(\frac(3) )(10) \höger))^(2))\]
\[((\left(((\left(\frac(10)(3) \right))^(3)) \right))^(x-1))=(\left(\frac(10) )(3) \höger))^(3\vänster(x-1 \höger)))=((\vänster(\frac(10)(3) \höger))^(3x-3))\]
Samtidigt, till höger, kan du också få en examen med samma bas, för vilken det räcker att bara "vända" bråket:
\[((\left(\frac(3)(10) \right))^(2))=((\left(\frac(10)(3) \right))^(-2))\]
Slutligen kommer vår ekvation att ta formen:
\[\begin(align)& ((\left(\frac(10)(3) \right))^(3x-3))=((\left(\frac(10)(3) \right)) ^(-2)); \\& 3x-3=-2; \\& 3x=1; \\& x=\frac(1)(3). \\\end(align)\]
Det är hela lösningen. Hans huvudtanke är att även om olika baser x vi försöker med krok eller skurk att reducera dessa grunder till en och samma. I detta har vi hjälp av elementära transformationer av ekvationer och reglerna för att arbeta med potenser.
Men vilka regler och när ska man använda? Hur förstår man att i en ekvation måste du dela båda sidor med något, och i en annan - för att bryta ner exponentialfunktionens bas i faktorer?
Svaret på denna fråga kommer med erfarenhet. Testa dig först enkla ekvationer, och sedan gradvis komplicera uppgifterna - och mycket snart kommer dina färdigheter att räcka för att lösa alla exponentiella ekvationer från samma ANVÄNDNING eller något oberoende / testarbete.
Och för att hjälpa dig i denna svåra uppgift, föreslår jag att ladda ner en uppsättning ekvationer på min hemsida oberoende beslut. Alla ekvationer har svar, så du kan alltid kontrollera dig själv.
Föreläsning: "Metoder för att lösa exponentiella ekvationer."
1 . exponentiella ekvationer.
Ekvationer som innehåller okända i exponenten kallas exponentiella ekvationer. Den enklaste av dessa är ekvationen ax = b, där a > 0 och a ≠ 1.
1) För b< 0 и b = 0 это уравнение, согласно свойству 1 показательной функции, не имеет решения.
2) För b > 0, med funktionens monotoni och rotsatsen, har ekvationen en enda rot. För att hitta den måste b representeras som b = aс, ax = bс ó x = c eller x = logab.
De exponentiella ekvationerna, genom algebraiska transformationer, leder till standardekvationer, som löses med följande metoder:
1) metod för reduktion till en bas;
2) utvärderingsmetod;
3) grafisk metod;
4) metoden för att introducera nya variabler;
5) faktoriseringsmetod;
6) exponentiell - potensekvationer;
7) exponentiell med en parameter.
2 . Metod för minskning till en bas.
Metoden bygger på nästa fastighet grader: om två grader är lika och deras baser är lika, så är deras exponenter lika, dvs. ekvationen måste försöka reduceras till formen
Exempel. Lös ekvationen:
1 . 3x=81;
Låt oss representera den högra sidan av ekvationen i formen 81 = 34 och skriv ekvationen som motsvarar den ursprungliga 3 x = 34; x = 4. Svar: 4.
2. https://pandia.ru/text/80/142/images/image004_8.png" width="52" height="49"> och gå till ekvationen för exponenter 3x+1 = 3 – 5x; 8x = 4; x = 0,5 Svar: 0,5
3. https://pandia.ru/text/80/142/images/image006_8.png" width="105" height="47">
Observera att siffrorna 0,2, 0,04, √5 och 25 är 5 potenser. Låt oss dra fördel av detta och transformera den ursprungliga ekvationen enligt följande:
![]() ,
varav 5-x-1 = 5-2x-2 ó - x - 1 = - 2x - 2, från vilken vi finner lösningen x = -1. Svar: -1.
,
varav 5-x-1 = 5-2x-2 ó - x - 1 = - 2x - 2, från vilken vi finner lösningen x = -1. Svar: -1.
5. 3x = 5. Per definition av logaritmen, x = log35. Svar: log35.
6. 62x+4 = 33x. 2x+8.
Låt oss skriva om ekvationen till 32x+4,22x+4 = 32x.2x+8, dvs..png" width="181" height="49 src="> Därav x - 4 =0, x = 4. Svar: 4.
7 . 2∙3x+1 - 6∙3x-2 - 3x = 9. Med hjälp av potensernas egenskaper skriver vi ekvationen på formen e. x+1 = 2, x =1. Svar: 1.


Uppgiftsbank nr 1.
Lös ekvationen:
Test nummer 1.
1) 0 2) 4 3) -2 4) -4 |
|
A2 32x-8 = √3. | 1)17/4 2) 17 3) 13/2 4) -17/4 |
A3 | 1) 3;1 2) -3;-1 3) 0;2 4) inga rötter |
1) 7;1 2) inga rötter 3) -7;1 4) -1;-7 |
|
A5 | 1) 0;2; 2) 0;2;3 3) 0 4) -2;-3;0 |
A6 | 1) -1 2) 0 3) 2 4) 1 |
Test #2
A1 | 1) 3 2) -1;3 3) -1;-3 4) 3;-1 |
A2 | 1) 14/3 2) -14/3 3) -17 4) 11 |
A3 | 1) 2;-1 2) inga rötter 3) 0 4) -2;1 |
A4 | 1) -4 2) 2 3) -2 4) -4;2 |
A5 | 1) 3 2) -3;1 3) -1 4) -1;3 |
3 Bedömningsmetod.
Rotsatsen: om funktionen f (x) ökar (minskar) på intervallet I, är talet a vilket värde som tas av f på detta intervall, då har ekvationen f (x) = a en enda rot på intervallet I.
Vid lösning av ekvationer med skattningsmetoden används denna sats och funktionens monotoniegenskaper.
Exempel. Lös ekvationer: 1. 4x = 5 - x.
Lösning. Låt oss skriva om ekvationen som 4x + x = 5.
1. om x \u003d 1, då 41 + 1 \u003d 5, 5 \u003d 5 är sant, då är 1 roten till ekvationen.
Funktionen f(x) = 4x ökar på R och g(x) = x ökar på R => h(x)= f(x)+g(x) ökar på R som summan av ökande funktioner, så x = 1 är den enda roten av ekvationen 4x = 5 – x. Svar: 1.
2.

Lösning. Vi skriver om ekvationen i formen  .
.
1. om x = -1, då ![]() , 3 = 3-sant, så x = -1 är roten till ekvationen.
, 3 = 3-sant, så x = -1 är roten till ekvationen.
2. bevisa att det är unikt.
3. Funktionen f(x) = - minskar på R, och g(x) = - x - minskar på R => h(x) = f(x) + g(x) - minskar på R, eftersom summan av minskande funktioner. Så enligt rotsatsen är x = -1 den enda roten i ekvationen. Svar: -1.
Uppgiftsbank nr 2. lösa ekvationen

a) 4x + 1 = 6-x;
b) 
c) 2x - 2 = 1 - x;
4. Metod för att introducera nya variabler.
Metoden beskrivs i avsnitt 2.1. Införandet av en ny variabel (substitution) utförs vanligtvis efter transformationer (förenklingar) av termerna i ekvationen. Tänk på exempel.
Exempel.
Räta ekvation: 1.
![]() .
.
Låt oss skriva om ekvationen annorlunda: https://pandia.ru/text/80/142/images/image030_0.png" width="128" height="48 src="> i.e..png" width="210" height = "45">
Lösning. Låt oss skriva om ekvationen annorlunda: 
Ange https://pandia.ru/text/80/142/images/image035_0.png" width="245" height="57"> - inte lämplig.
t = 4 => https://pandia.ru/text/80/142/images/image037_0.png" width="268" height="51"> är en irrationell ekvation. Observera att 
Lösningen till ekvationen är x = 2,5 ≤ 4, så 2,5 är roten till ekvationen. Svar: 2.5.
Lösning. Låt oss skriva om ekvationen i formen och dividera båda sidorna med 56x+6 ≠ 0. Vi får ekvationen

2x2-6x-7 = 2x2-6x-8 +1 = 2(x2-3x-4)+1, alltså..png" width="118" height="56">
Rötterna till andragradsekvationen - t1 = 1 och t2<0, т. е..png" width="200" height="24">.
Lösning . Vi skriver om ekvationen i formen
och notera att det är en homogen ekvation av andra graden.
Dividera ekvationen med 42x, vi får 
Ersätt https://pandia.ru/text/80/142/images/image049_0.png" width="16" height="41 src="> .

Svar: 0; 0,5.
Uppgiftsbank #3. lösa ekvationen
b) ![]()
G) ![]()
Test #3 med ett urval av svar. Lägsta nivå.
A1 | 1) -0,2;2 2) log52 3) –log52 4) 2 |
А2 0,52x – 3 0,5x +2 = 0. | 1) 2;1 2) -1;0 3) inga rötter 4) 0 |
1) 0 2) 1; -1/3 3) 1 4) 5 |
|
A4 52x-5x - 600 = 0. | 1) -24;25 2) -24,5; 25,5 3) 25 4) 2 |
1) inga rötter 2) 2;4 3) 3 4) -1;2 |
Test #4 med ett urval av svar. Allmän nivå.
A1 | 1) 2;1 2) ½;0 3)2;0 4) 0 |
А2 2x – (0,5)2x – (0,5)x + 1 = 0 | 1) -1;1 2) 0 3) -1;0;1 4) 1 |
1) 64 2) -14 3) 3 4) 8 |
|
1)-1 2) 1 3) -1;1 4) 0 |
|
A5 | 1) 0 2) 1 3) 0;1 4) inga rötter |
5. Metod för faktorisering.
1. Lös ekvationen: 5x+1 - 5x-1 = 24.
Lösning..png" width="169" height="69"> , varifrån
2. 6x + 6x+1 = 2x + 2x+1 + 2x+2.
Lösning. Låt oss ta ut 6x på vänster sida av ekvationen och 2x på höger sida. Vi får ekvationen 6x(1+6) = 2x(1+2+4) ó 6x = 2x.
Eftersom 2x >0 för alla x, kan vi dividera båda sidor av denna ekvation med 2x utan rädsla för att förlora lösningar. Vi får 3x = 1ó x = 0.
3. ![]()
Lösning. Vi löser ekvationen genom att faktorisera.
Vi väljer kvadraten på binomialen 
4. https://pandia.ru/text/80/142/images/image067_0.png" width="500" height="181">
x = -2 är roten till ekvationen.
Ekvation x + 1 = 0 " style="border-collapse:collapse;border:none">
A1 5x-1 +5x -5x+1 = -19.
1) 1 2) 95/4 3) 0 4) -1
A2 3x+1 +3x-1 =270.
1) 2 2) -4 3) 0 4) 4
A3 32x + 32x+1 -108 = 0. x=1,5
1) 0,2 2) 1,5 3) -1,5 4) 3
1) 1 2) -3 3) -1 4) 0
A5 2x -2x-4 = 15,x=4
1) -4 2) 4 3) -4;4 4) 2
Test #6 Allmän nivå.
A1 (22x-1)(24x+22x+1)=7. | 1) ½ 2) 2 3) -1; 3 4) 0,2 |
A2 | 1) 2,5 2) 3;4 3) log43/2 4) 0 |
A3 2x-1-3x=3x-1-2x+2. | 1) 2 2) -1 3) 3 4) -3 |
A4 | 1) 1,5 2) 3 3) 1 4) -4 |
A5 | 1) 2 2) -2 3) 5 4) 0 |
6. Exponentiell - potensekvationer.
Exponentiella ekvationer angränsas av de så kallade exponentialpotensekvationerna, dvs ekvationer av formen (f(x))g(x) = (f(x))h(x).
Om man vet att f(x)>0 och f(x) ≠ 1, så löses ekvationen, liksom den exponentiella, genom att likställa exponenterna g(x) = f(x).
Om villkoret inte utesluter möjligheten för f(x)=0 och f(x)=1, måste vi ta hänsyn till dessa fall när vi löser exponentialpotensekvationen.
1..png" width="182" height="116 src=">
2. ![]()
Lösning. x2 +2x-8 - är vettigt för alla x, eftersom ett polynom, så ekvationen är ekvivalent med mängden
 https://pandia.ru/text/80/142/images/image078_0.png" width="137" height="35">
https://pandia.ru/text/80/142/images/image078_0.png" width="137" height="35">
b) ![]()
7. Exponentiella ekvationer med parametrar.
1. För vilka värden av parametern p har ekvationen 4 (5 – 3) 2 +4p2–3p = 0 (1) en unik lösning?
Lösning. Låt oss introducera förändringen 2x = t, t > 0, då kommer ekvation (1) att ha formen t2 – (5p – 3)t + 4p2 – 3p = 0. (2)
Diskriminanten i ekvation (2) är D = (5p – 3)2 – 4(4p2 – 3p) = 9(p – 1)2.
Ekvation (1) har en unik lösning om ekvation (2) har en positiv rot. Detta är möjligt i följande fall.
1. Om D = 0, det vill säga p = 1, kommer ekvation (2) att ha formen t2 – 2t + 1 = 0, därav t = 1, därför har ekvation (1) en unik lösning x = 0.
2. Om p1, då 9(p – 1)2 > 0, så har ekvation (2) två olika rötter t1 = p, t2 = 4p – 3. Systemuppsättningen uppfyller problemets villkor

Att ersätta t1 och t2 i systemen har vi


https://pandia.ru/text/80/142/images/image084_0.png" alt="(!LANG:no35_11" width="375" height="54"> в зависимости от параметра a?!}
Lösning. Låt vara  då kommer ekvation (3) att ha formen t2 – 6t – a = 0. (4)
då kommer ekvation (3) att ha formen t2 – 6t – a = 0. (4)
Låt oss hitta värdena för parametern a för vilken minst en rot av ekvation (4) uppfyller villkoret t > 0.
Låt oss introducera funktionen f(t) = t2 – 6t – a. Följande fall är möjliga.
https://pandia.ru/text/80/142/images/image087.png" alt="(!LANG:http://1september.ru/ru/mat/2002/35/no35_14.gif" align="left" width="215" height="73 src=">где t0 - абсцисса вершины параболы и D - дискриминант квадратного трехчлена f(t);!}
https://pandia.ru/text/80/142/images/image089.png" alt="(!LANG:http://1september.ru/ru/mat/2002/35/no35_16.gif" align="left" width="60" height="51 src=">!}
Fall 2. Ekvation (4) har en unik positiv lösning om
D = 0, om a = – 9, kommer ekvation (4) att ha formen (t – 3)2 = 0, t = 3, x = – 1.
Fall 3. Ekvation (4) har två rötter, men en av dem uppfyller inte olikheten t > 0. Detta är möjligt om
 https://pandia.ru/text/80/142/images/image092.png" alt="(!LANG:no35_17" width="267" height="63">!}
https://pandia.ru/text/80/142/images/image092.png" alt="(!LANG:no35_17" width="267" height="63">!}
Således, vid a 0 har ekvation (4) en enda positiv rot ![]() . Då har ekvation (3) en unik lösning
. Då har ekvation (3) en unik lösning 
För en< – 9 уравнение (3) корней не имеет.
 Om en< – 9, то корней нет; если – 9 < a < 0, то
Om en< – 9, то корней нет; если – 9 < a < 0, то
om a = – 9, då x = – 1;
om a 0, då

Låt oss jämföra metoderna för att lösa ekvationerna (1) och (3). Observera att när ekvation (1) löstes reducerades till en andragradsekvation, vars diskriminant är en hel kvadrat; således beräknades rötterna till ekvation (2) omedelbart med formeln för rötter till andragradsekvationen, och sedan drogs slutsatser om dessa rötter. Ekvation (3) reducerades till en andragradsekvation (4), vars diskriminant inte är en perfekt kvadrat, därför är det, när man löser ekvation (3), tillrådligt att använda satser om placeringen av rötterna till ett kvadrattrinomial och en grafisk modell. Observera att ekvation (4) kan lösas med hjälp av Vieta-satsen.
Låt oss lösa mer komplexa ekvationer.
Uppgift 3. Lös ekvationen ![]()
Lösning. ODZ: x1, x2.
Låt oss introducera en ersättare. Låt 2x = t, t > 0, då som ett resultat av transformationer kommer ekvationen att ta formen t2 + 2t – 13 – a = 0. (*) Låt oss hitta värdena på a för vilka minst en rot av ekvationen (*) uppfyller villkoret t > 0.
https://pandia.ru/text/80/142/images/image098.png" alt="(!LANG:http://1september.ru/ru/mat/2002/35/no35_23.gif" align="left" width="71" height="68 src=">где t0 - абсцисса вершины f(t) = t2 + 2t – 13 – a, D - дискриминант квадратного трехчлена f(t).!}
https://pandia.ru/text/80/142/images/image100.png" alt="(!LANG:http://1september.ru/ru/mat/2002/35/no35_25.gif" align="left" width="360" height="32 src=">!}
https://pandia.ru/text/80/142/images/image102.png" alt="(!LANG:http://1september.ru/ru/mat/2002/35/no35_27.gif" align="left" width="218" height="42 src=">!}
Svar: om a > - 13, a 11, a 5, då om a - 13,
a = 11, a = 5, då finns det inga rötter.
Bibliografi.
1. Guzeevs grunder för utbildningsteknologi.
2. Guzeev-teknik: från reception till filosofi.
M. "Rektor" nr 4, 1996
3. Guzeev och organisatoriska utbildningsformer.
4. Guzeev och utövandet av integrerad pedagogisk teknologi.
M. "Folkets utbildning", 2001
5. Guzeev från formerna för lektionen - seminarium.
Matematik i skolan nr 2, 1987, s. 9 - 11.
6. Selevko utbildningsteknologier.
M. "Folkets utbildning", 1998
7. Episheva skolbarn lär sig matematik.
M. "Enlightenment", 1990
8. Ivanov för att förbereda lektioner - workshops.
Matematik i skolan nr 6, 1990, sid. 37-40.
9. Smirnov modell för undervisning i matematik.
Matematik i skolan nr 1, 1997, sid. 32-36.
10. Tarasenko sätt att organisera praktiskt arbete.
Matematik i skolan nr 1, 1993, sid. 27 - 28.
11. Om en av typerna av individuellt arbete.
Matematik i skolan nr 2, 1994, s. 63 - 64.
12. Khazankins kreativa förmågor hos skolbarn.
Matematik i skolan nr 2, 1989, sid. 10.
13. Scanavi. Förlag, 1997
14. et al. Algebra och början av analys. Didaktiskt material för
15. Krivonogov uppgifter i matematik.
M. "Första september", 2002
16. Tjerkasov. Handbok för gymnasieelever och
komma in på universiteten. "A S T - pressskola", 2002
17. Zhevnyak för sökande till universitet.
Minsk och RF "Review", 1996
18. Skriftlig D. Förberedelse inför tentamen i matematik. M. Rolf, 1999
19. mfl. Lära sig lösa ekvationer och ojämlikheter.
M. "Intellekt - Center", 2003
20. och andra. Utbildnings- och träningsmaterial för att förbereda E G E.
M. "Intellekt - Center", 2003 och 2004
21 och andra Varianter av CMM. Testcenter vid Ryska federationens försvarsministerium, 2002, 2003
22. Goldbergs ekvationer. "Quantum" nr 3, 1971
23. Volovich M. Hur man framgångsrikt undervisar i matematik.
Matematik, 1997 nr 3.
24 Okunev för lektionen, barn! M. Enlightenment, 1988
25. Yakimanskaya - orienterad utbildning i skolan.
26. Liimets arbetar på lektionen. M. Kunskap, 1975
Första nivån
exponentiella ekvationer. Omfattande guide (2019)
Hallå! Idag kommer vi att diskutera med dig hur man löser ekvationer som kan vara både elementära (och jag hoppas att efter att ha läst den här artikeln kommer nästan alla att vara det för dig), och de som vanligtvis ges "återfyllning". Tydligen att somna helt. Men jag ska försöka göra mitt bästa så att du nu inte hamnar i trubbel när du ställs inför den här typen av ekvationer. Jag kommer inte längre att slå runt, men jag kommer genast att öppna liten hemlighet: idag ska vi jobba exponentiella ekvationer.
Innan jag går vidare till en analys av sätten att lösa dem kommer jag omedelbart att beskriva en cirkel av frågor (ganska liten) för dig som du bör upprepa innan du skyndar dig att storma detta ämne. Så för bästa resultat, tack upprepa:
- fastigheter och
- Lösning och ekvationer
Upprepad? Fantastisk! Då blir det inte svårt för dig att lägga märke till att roten till ekvationen är ett tal. Är du säker på att du förstår hur jag gjorde det? Sanning? Sedan fortsätter vi. Svara nu på frågan, vad är lika med tredje potensen? Du har helt rätt: . Åtta är vilken kraft av två? Just det - den tredje! Eftersom. Nåväl, låt oss nu försöka lösa följande problem: Låt mig multiplicera talet med sig själv en gång och få resultatet. Frågan är, hur många gånger har jag multiplicerat med mig själv? Du kan självklart kolla detta direkt:
\begin(align) & 2=2 \\ & 2\cdot 2=4 \\ & 2\cdot 2\cdot 2=8 \\ & 2\cdot 2\cdot 2\cdot 2=16 \\ \end( justera)
Då kan du dra slutsatsen att jag multiplicerade gånger av sig själv. Hur kan detta annars verifieras? Och så här: direkt enligt definitionen av examen: . Men, måste du erkänna, om jag frågade hur många gånger två måste multipliceras med sig själv för att få, säg, du skulle säga till mig: Jag kommer inte att lura mig själv och multiplicera med mig själv tills jag är blå i ansiktet. Och han skulle ha helt rätt. För hur kan du skriv ner alla åtgärder kortfattat(och korthet är talangens syster)
var - det här är själva "tider" när du multiplicerar med sig själv.
Jag tror att du vet (och om du inte vet, brådskande, mycket brådskande upprepa graderna!) att då kommer mitt problem att skrivas i formen:
Hur kan du rimligen dra slutsatsen att:
Så, tyst, skrev jag ner det enklaste exponentiell ekvation:
Och till och med hittat den rot. Tycker du inte att allt är ganska trivialt? Det är precis vad jag tycker också. Här är ett annat exempel för dig:
Men vad ska man göra? Det kan trots allt inte skrivas som en grad av ett (rimligt) tal. Låt oss inte misströsta och notera att båda dessa siffror är perfekt uttryckta i termer av kraften i samma nummer. Vad? Höger: . Sedan omvandlas den ursprungliga ekvationen till formen:
Varifrån, som du redan förstått, . Låt oss inte dra längre och skriva ner definition:
I vårt fall med dig: .
Dessa ekvationer löses genom att reducera dem till formen:
med efterföljande lösning av ekvationen
Vi gjorde faktiskt detta i föregående exempel: vi fick det. Och vi löste den enklaste ekvationen med dig.
Det verkar inte vara något komplicerat, eller hur? Låt oss öva på det enklaste först. exempel:
Vi ser återigen att höger och vänster sida av ekvationen måste representeras som en potens av ett tal. Visserligen har detta redan gjorts till vänster, men till höger finns det ett nummer. Men, det är okej, trots allt, och min ekvation förvandlas mirakulöst till detta:
Vad behövde jag göra här? Vilken regel? Makt till makt regel som lyder:
Tänk om:
Innan vi svarar på denna fråga, låt oss fylla i följande tabell med dig:
Det är inte svårt för oss att lägga märke till att ju mindre, desto mindre mindre värde, men ändå är alla dessa värden större än noll. OCH DET KOMMER ALLTID ATT VARA SÅ!!! Samma egenskap gäller FÖR ALLA BAS MED NÅGOT INDEX!! (för alla och). Vad kan vi då dra för slutsatsen om ekvationen? Och här är en: den har inga rötter! Precis som alla ekvationer inte har några rötter. Nu ska vi träna och Låt oss lösa några enkla exempel:
Låt oss kolla:
1. Ingenting krävs av dig här, förutom att du känner till makternas egenskaper (vilket jag förresten bad dig att upprepa!) Som regel leder allt till den minsta basen: , . Då kommer den ursprungliga ekvationen att motsvara följande: Allt jag behöver är att använda egenskaperna för potenser: när man multiplicerar tal med samma bas adderas exponenterna och vid division subtraheras de. Då får jag: Nåväl, nu kommer jag med gott samvete att gå från exponentialekvationen till den linjära: \begin(align)
& 2x+1+2(x+2)-3x=5 \\
& 2x+1+2x+4-3x=5 \\
&x=0. \\
\end(align)
2. I det andra exemplet måste du vara mer försiktig: problemet är att på vänster sida kommer vi inte att kunna representera samma tal som en potens. I det här fallet är det ibland användbart representerar tal som en produkt av potenser med olika baser, men samma exponenter:
Den vänstra sidan av ekvationen kommer att ha formen: Vad gav detta oss? Och här är vad: Tal med olika baser men samma exponent kan multipliceras.I det här fallet multipliceras baserna, men exponenten ändras inte:
Tillämpat på min situation kommer detta att ge:
\begin(align)
& 4\cdot ((64)^(x))((25)^(x))=6400, \\
& 4\cdot (((64\cdot 25))^(x))=6400, \\
& ((1600)^(x))=\frac(6400)(4), \\
& ((1600)^(x))=1600, \\
&x=1. \\
\end(align)
Inte illa, eller hur?
3. Jag gillar inte när jag har två termer på ena sidan av ekvationen, och ingen på den andra (ibland är det förstås motiverat, men så är det inte nu). Flytta minustermen åt höger:
Nu, som tidigare, kommer jag att skriva allt genom trippelns krafter:
Jag lägger till potenserna till vänster och får en ekvation motsvarande
Du kan enkelt hitta dess rot:
4. Som i exempel tre, termen med minus - en plats på höger sida!
Till vänster är nästan allt bra med mig, förutom vad? Ja, "fel grad" av tvåan stör mig. Men jag kan enkelt fixa detta genom att skriva: . Eureka - till vänster är alla baser olika, men alla grader är lika! Vi förökar oss snabbt!
Här är allt klart igen: (om du inte förstod hur jag magiskt fick den sista jämställdheten, ta en paus en minut, ta en paus och läs examens egenskaper igen mycket noga. Vem sa att du kan hoppa över grad med en negativ exponent? Tja, här är jag ungefär som ingen). Nu ska jag få:
\begin(align)
& ((2)^(4\vänster((x) -9 \höger)))=((2)^(-1)) \\
&4((x) -9)=-1 \\
&x=\frac(35)(4). \\
\end(align)
Här är uppgifterna för dig att öva på, som jag bara kommer att ge svaren på (men i en "blandad" form). Lös dem, kolla så fortsätter vi vår forskning!
Redo? Svar som dessa:
- vilket nummer som helst
Okej, okej, jag skojade! Här är konturerna av lösningarna (en del är ganska korta!)
Tror du inte att det är ingen slump att en bråkdel till vänster är en "omvänd" annan? Det skulle vara synd att inte använda detta:
Denna regel används väldigt ofta när man löser exponentialekvationer, kom ihåg det väl!
Då blir den ursprungliga ekvationen:
Löser det andragradsekvation, får du följande rötter:
2. En annan lösning: dividera båda delarna av ekvationen med uttrycket till vänster (eller höger). Jag delar med det som finns till höger, då får jag:
Var (varför?!)
3. Jag vill inte ens upprepa mig själv, allt har redan "tuggats" så mycket.
4. ekvivalent med en andragradsekvation, rötterna
5. Du måste använda formeln i den första uppgiften, då får du det:
Ekvationen har förvandlats till en trivial identitet, vilket är sant för alla. Då är svaret valfritt reellt tal.
Nåväl, här är du och tränade på att bestämma dig de enklaste exponentiella ekvationerna. Nu vill jag ge dig några livsexempel, vilket hjälper dig att förstå varför de behövs i princip. Här ska jag ge två exempel. En av dem är ganska vardaglig, men den andra är mer av vetenskapligt än praktiskt intresse.
Exempel 1 (merkantilt) Låt dig ha rubel, men du vill förvandla det till rubel. Banken erbjuder dig att ta dessa pengar från dig till en årlig ränta med en månatlig kapitalisering av ränta (månatlig periodisering). Frågan är, hur många månader behöver du öppna en insättning för att få ut det önskade slutbeloppet? En ganska vardaglig uppgift, eller hur? Ändå är dess lösning kopplad till konstruktionen av motsvarande exponentiella ekvation: Låt - det initiala beloppet, - det slutliga beloppet, - räntan för perioden, - antalet perioder. Sedan:
I vårt fall (om kursen är per år, så beräknas den per månad). Varför är det uppdelat i? Om du inte vet svaret på denna fråga, kom ihåg ämnet ""! Då får vi följande ekvation:
Denna exponentiella ekvation kan redan lösas endast med en miniräknare (dess utseende antyder detta, och detta kräver kunskap om logaritmer, som vi kommer att bekanta oss med lite senare), vilket jag kommer att göra: ... För att få en miljon behöver vi alltså göra en insättning i en månad (ej väldigt snabbt, eller hur?).
Exempel 2 (ganska vetenskapligt). Trots hans, viss "isolering", rekommenderar jag att du uppmärksammar honom: han "glidar regelbundet in på tentan!! (uppgiften är hämtad från den "riktiga" versionen) Under sönderfallet av en radioaktiv isotop minskar dess massa enligt lagen, där (mg) är isotopens initiala massa, (min.) är tiden som förflutit från initialt ögonblick, (min.) är halveringstiden. I det första ögonblicket är massan av isotopen mg. Dess halveringstid är min. Om hur många minuter kommer massan av isotopen att vara lika med mg? Det är okej: vi tar bara och ersätter all data i formeln som föreslås oss:
Låt oss dela båda delarna med "i hopp om att vi till vänster får något smältbart:
Nåväl, vi har väldigt tur! Den står till vänster, låt oss sedan gå vidare till motsvarande ekvation:
Där min.
Som du kan se har exponentiella ekvationer en mycket verklig tillämpning i praktiken. Nu vill jag diskutera med dig ett annat (enkelt) sätt att lösa exponentiella ekvationer, som bygger på att ta den gemensamma faktorn ur parentes och sedan gruppera termerna. Var inte rädd för mina ord, du har redan stött på den här metoden i 7:an när du studerade polynom. Till exempel, om du behövde faktorisera uttrycket:
Låt oss gruppera: den första och tredje termen, såväl som den andra och fjärde. Det är tydligt att den första och den tredje är skillnaden mellan kvadraterna:
och den andra och fjärde har en gemensam faktor på tre:
Då motsvarar det ursprungliga uttrycket detta:
Det är inte längre svårt att ta ut den gemensamma faktorn:
Följaktligen,
Ungefär så här kommer vi att agera när vi löser exponentiella ekvationer: leta efter "commonality" bland termerna och ta bort det från parentes, och sedan - vad som än händer, jag tror att vi kommer att ha tur =)) Till exempel:
Till höger är långt ifrån makten sju (jag kollade!) Och till vänster - lite bättre kan du naturligtvis "hacka av" faktorn a från den första termen och från den andra, och sedan ta itu med vad du har, men låt oss göra mer försiktigt med dig. Jag vill inte ta itu med de fraktioner som oundvikligen produceras av "selektion", så borde jag inte ha det bättre att hålla ut? Då har jag inte bråkdelar: som de säger, både vargarna är mätta och fåren är säkra:
Räkna uttrycket inom parentes. Magiskt, magiskt visar det sig att (överraskande, även om vad mer kan vi förvänta oss?).
Sedan reducerar vi båda sidor av ekvationen med denna faktor. Vi får: var.
Här är ett mer komplicerat exempel (ganska lite, egentligen):
Här är problemet! Vi har ingen gemensam grund här! Det är inte helt klart vad man ska göra nu. Och låt oss göra vad vi kan: för det första kommer vi att flytta "fyrorna" i en riktning och "femman" i den andra:
Låt oss nu ta ut det "vanliga" till vänster och höger:
Så vad nu? Vad är fördelen med en sådan dum gruppering? Vid första anblicken syns det inte alls, men låt oss titta djupare:
Nåväl, låt oss nu göra det så att vi till vänster bara har uttrycket c, och till höger - allt annat. Hur kan vi göra det? Och så här: Dividera båda sidor av ekvationen först med (så att vi blir av med exponenten till höger), och dividera sedan båda sidor med (så att vi blir av med den numeriska faktorn till vänster). Äntligen får vi:
Otrolig! Till vänster har vi ett uttryck, och till höger - bara. Då drar vi genast slutsatsen att
Här är ett annat exempel att förstärka:
Jag tar med honom kort lösning(inte riktigt bry sig om att förklara), försök ta reda på alla "finesser" i lösningen själv.
Nu är den slutliga konsolideringen av materialet som omfattas. Försök att lösa följande problem på egen hand. Jag kommer bara att ge korta rekommendationer och tips för att lösa dem:
- Låt oss ta den gemensamma faktorn utanför parentes:
- Vi representerar det första uttrycket i formen: , dividera båda delarna med och få det
- , sedan omvandlas den ursprungliga ekvationen till formen: Nåväl, nu ett tips - leta efter var du och jag redan har löst denna ekvation!
- Föreställ dig hur, hur, ah, ja, dividera sedan båda delarna med, så att du får den enklaste exponentiella ekvationen.
- Ta bort det från parentes.
- Ta bort det från parentes.
EXPOSITIONSEKVATIONER. GENOMSNITTLIG NIVÅ
Jag antar att efter att ha läst den första artikeln, som berättade vad är exponentiella ekvationer och hur man löser dem du har bemästrat nödvändigt minimum kunskap som behövs för att lösa enkla exempel.
Nu ska jag analysera en annan metod för att lösa exponentiella ekvationer, det här är
"metod för att introducera en ny variabel" (eller substitution). Han löser de flesta av de "svåra" problemen, på ämnet exponentiella ekvationer (och inte bara ekvationer). Denna metod är en av de mest använda i praktiken. Först rekommenderar jag att du bekantar dig med ämnet.
Som du redan förstått av namnet är kärnan i denna metod att introducera en sådan förändring av variabeln att din exponentiella ekvation mirakulöst kommer att förvandlas till en som du redan lätt kan lösa. Allt som återstår för dig efter att ha löst denna mycket "förenklade ekvation" är att göra en "omvänd ersättning": det vill säga att gå tillbaka från det ersatta till det ersatta. Låt oss illustrera vad vi just sa med ett mycket enkelt exempel:
Exempel 1:
Denna ekvation löses genom en "enkel substitution", som matematiker nedsättande kallar det. I själva verket är substitutionen här den mest uppenbara. Det måste bara ses
Då blir den ursprungliga ekvationen:
Om vi dessutom föreställer oss hur, så är det helt klart vad som behöver bytas ut: naturligtvis . Vad blir då den ursprungliga ekvationen? Och här är vad:
Du kan enkelt hitta dess rötter på egen hand:. Vad ska vi göra nu? Det är dags att återgå till den ursprungliga variabeln. Vad har jag glömt att ta med? Nämligen: när man ersätter en viss grad med en ny variabel (det vill säga när man ersätter en typ) kommer jag att vara intresserad av bara positiva rötter! Du kan själv enkelt svara på varför. Således är vi inte intresserade av dig, men den andra roten är ganska lämplig för oss:
Var då.
Svar:
Som du kan se, i det föregående exemplet, bad ersättaren om våra händer. Tyvärr är det inte alltid så. Låt oss dock inte gå direkt till det sorgliga, utan öva på ytterligare ett exempel med en ganska enkel ersättning
Exempel 2
Det är klart att det med största sannolikhet kommer att bli nödvändigt att ersätta (detta är den minsta av krafterna som ingår i vår ekvation), men innan vi introducerar en ersättning måste vår ekvation "förberedas" för det, nämligen: , . Sedan kan du ersätta, som ett resultat får jag följande uttryck:
Åh skräck: en kubisk ekvation med helt fruktansvärda formler för sin lösning (ja, tala in allmän syn). Men låt oss inte direkt misströsta utan fundera på vad vi ska göra. Jag kommer att föreslå fusk: vi vet att för att få ett "vackert" svar måste vi få lite trestyrka (varför skulle det vara det, va?). Och låt oss försöka gissa åtminstone en rot av vår ekvation (jag börjar gissa från tre potenser).
Första gissningen. Är inte en rot. Ack och ah...
.
Den vänstra sidan är lika.
Höger del: !
Det finns! Gissade första roten. Nu blir det lättare!
Känner du till indelningsschemat "hörn"? Naturligtvis vet du, du använder det när du delar ett tal med ett annat. Men få människor vet att samma sak kan göras med polynom. Det finns ett underbart teorem:
Tillämpligt på min situation berättar det för mig vad som är delbart utan rest med. Hur går uppdelningen till? Det är hur:
Jag tittar på vilket monom jag ska multiplicera för att få klart, då:
Jag subtraherar det resulterande uttrycket från, jag får:
Nu, vad behöver jag multiplicera för att få? Det är klart att på, då får jag:
och subtrahera återigen det resulterande uttrycket från det återstående:
Väl sista steget, multiplicera med och subtrahera från det återstående uttrycket:
Hurra, uppdelningen är över! Vad har vi samlat på oss privat? Av sig själv: .
Sedan fick vi följande expansion av det ursprungliga polynomet:
Låt oss lösa den andra ekvationen:
Den har rötter:
Sedan den ursprungliga ekvationen:
har tre rötter:
Vi kasserar naturligtvis den sista roten, eftersom den är mindre än noll. Och de två första efter omvänd substitution kommer att ge oss två rötter:
Svar:..
Med det här exemplet ville jag inte alls skrämma dig, utan jag satte mig som mål att visa att även om vi hade en ganska enkel ersättare, så ledde det ändå till en ganska komplex ekvation, vars lösning krävde en del specialkunskaper från oss. Tja, ingen är immun mot detta. Men förändringen i det här fallet var ganska uppenbar.
Här är ett exempel med en något mindre uppenbar ersättning:
Det är inte alls klart vad vi ska göra: problemet är att i vår ekvation finns det två olika baser och den ena basen kan inte erhållas från den andra genom att höja den till någon (rimlig, naturligt) makt. Men vad ser vi? Båda baserna skiljer sig endast i tecken, och deras produkt är skillnaden mellan kvadrater lika med en:
Definition:
Således är talen som är baser i vårt exempel konjugerade.
I så fall skulle det smarta draget vara multiplicera båda sidor av ekvationen med det konjugerade talet.
Till exempel, på, då blir den vänstra sidan av ekvationen lika, och den högra sidan. Om vi gör en ersättning kommer vår ursprungliga ekvation med dig att bli så här:
dess rötter, alltså, men kommer vi ihåg det, vi förstår det.
Svar: , .
Som regel räcker ersättningsmetoden för att lösa de flesta "skolans" exponentiella ekvationer. Följande uppgifter är hämtade från USE C1 (ökad svårighetsgrad). Du är redan läskunnig nog att lösa dessa exempel på egen hand. Jag ger bara den ersättning som krävs.
- Lös ekvationen:
- Hitta rötterna till ekvationen:
- Lös ekvationen: . Hitta alla rötter till denna ekvation som hör till segmentet:
Nu till några snabba förklaringar och svar:
- Här räcker det med att notera att och. Då kommer den ursprungliga ekvationen att motsvara denna: Denna ekvation löses genom att ersätta Gör följande beräkningar själv. I slutändan kommer din uppgift att reduceras till att lösa den enklaste trigonometriska (beroende på sinus eller cosinus). Vi kommer att diskutera lösningen av sådana exempel i andra avsnitt.
- Här kan du till och med klara dig utan ersättning: det räcker att överföra subtrahenden till höger och representera båda baserna genom två potenser: och sedan omedelbart gå till andragradsekvationen.
- Den tredje ekvationen löses också på ett ganska standardiserat sätt: föreställ dig hur. När vi sedan ersätter får vi en andragradsekvation: sedan,
Vet du redan vad en logaritm är? Inte? Läs då ämnet snarast!
Den första roten tillhör uppenbarligen inte segmentet, och den andra är obegriplig! Men det får vi veta snart! Sedan (detta är en egenskap hos logaritmen!) Låt oss jämföra:
Subtrahera från båda delarna, då får vi:
Den vänstra sidan kan representeras som:
multiplicera båda sidor med:
kan då multipliceras med
Låt oss sedan jämföra:
sedan dess:
Då tillhör den andra roten det önskade intervallet
Svar:
Som du ser, valet av rötterna till exponentiella ekvationer kräver en ganska djup kunskap om logaritmers egenskaper, så jag råder dig att vara så försiktig som möjligt när du löser exponentialekvationer. Som ni vet, i matematik är allt sammankopplat! Som min mattelärare brukade säga: "Du kan inte läsa matematik som historia över en natt."
Som regel alla svårigheten att lösa problem C1 är just valet av ekvationens rötter. Låt oss öva med ett annat exempel:
Det är klart att själva ekvationen löses ganska enkelt. Efter att ha gjort substitutionen reducerar vi vår ursprungliga ekvation till följande:
Låt oss först titta på den första roten. Jämför och: sedan, då. (egenskapen för den logaritmiska funktionen, at). Då är det klart att den första roten inte heller hör till vårt intervall. Nu den andra roten: . Det är klart att (eftersom funktionen ökar). Det återstår att jämföra och
sedan, då, samtidigt. Därmed kan jag "driva en pinne" mellan och. Denna pinne är ett nummer. Det första uttrycket är mindre än och det andra är större än. Då är det andra uttrycket större än det första och roten tillhör intervallet.
Svar: .
Avslutningsvis, låt oss titta på ett annat exempel på en ekvation där ersättningen är ganska icke-standard:
Låt oss börja direkt med vad du kan göra, och vad - i princip kan du, men det är bättre att inte göra det. Det är möjligt - att representera allt genom krafterna tre, två och sex. Vart leder det? Ja, och kommer inte att leda till någonting: en samling grader, av vilka några kommer att vara ganska svåra att bli av med. Vad behövs då? Låt oss notera att a Och vad kommer det att ge oss? Och det faktum att vi kan minska beslutet detta exempel för att lösa en ganska enkel exponentialekvation! Låt oss först skriva om vår ekvation som:
Nu delar vi båda sidorna av den resulterande ekvationen i:
Eureka! Nu kan vi byta ut, vi får:
Nåväl, nu är det din tur att lösa problem för demonstration, och jag kommer bara att ge dem korta kommentarer så att du inte går vilse! Lycka till!
1. Det svåraste! Att se en ersättare här är åh, vad fult! Ändå kan detta exempel lösas helt med hjälp av urval av en hel fyrkant. För att lösa det räcker det att notera att:
Så här är din ersättare:
(Observera att här, med vår ersättare, kan vi inte kasta bort den negativa roten!!! Och varför, vad tror du?)
Nu, för att lösa exemplet, måste du lösa två ekvationer:
Båda löses av "standardersättningen" (men den andra i ett exempel!)
2. Lägg märke till det och gör ett byte.
3. Expandera talet till coprime-faktorer och förenkla det resulterande uttrycket.
4. Dividera bråkets täljare och nämnare med (eller om du föredrar det) och gör ersättningen eller.
5. Observera att siffrorna och är konjugerade.
EXPOSITIONSEKVATIONER. AVANCERAD NIVÅ
Dessutom, låt oss titta på ett annat sätt - lösning av exponentialekvationer med logaritmmetoden. Jag kan inte säga att lösningen av exponentiella ekvationer med denna metod är mycket populär, men i vissa fall kan det bara leda oss till rätt beslut vår ekvation. Särskilt ofta används det för att lösa den så kallade " blandade ekvationer': det vill säga de där det finns funktioner av olika slag.
Till exempel, en ekvation som:
i allmänt fall kan bara lösas genom att ta logaritmen för båda delarna (till exempel med bas), där den ursprungliga ekvationen blir till följande:
Låt oss överväga följande exempel:
Det är tydligt att vi bara är intresserade av ODZ för den logaritmiska funktionen. Detta följer dock inte bara av ODZ för logaritmen, utan av en annan anledning. Jag tror att det inte kommer att vara svårt för dig att gissa vilken.
Låt oss ta logaritmen för båda sidor av vår ekvation till basen:
Som du kan se ledde logaritmen av vår ursprungliga ekvation oss snabbt till det korrekta (och vackra!) svaret. Låt oss öva med ett annat exempel:
Inte heller här finns det något att oroa sig för: vi tar logaritmen för båda sidor av ekvationen i termer av basen, då får vi:
Låt oss byta ut:
Men vi missade något! Har du märkt var jag gjorde ett misstag? När allt kommer omkring, då:
som inte uppfyller kravet (tänk var det kom ifrån!)
Svar:
Försök att skriva ner lösningen av exponentialekvationerna nedan:
Kontrollera nu din lösning med detta:
1. Vi logaritmer båda delarna till basen, givet att:
(den andra roten passar oss inte på grund av bytet)
2. Logaritm till basen:
Låt oss omvandla det resulterande uttrycket till följande form:
EXPOSITIONSEKVATIONER. KORT BESKRIVNING OCH GRUNDFORMEL
exponentiell ekvation
Typ ekvation:
kallad den enklaste exponentiella ekvationen.
Examensegenskaper
Lösningsmetoder
- Casting till samma grund
- Reduktion till samma exponent
- Variabel substitution
- Förenkla uttrycket och använd något av ovanstående.








 Balabol, balabolit, blah blah - etymologi Balabol som betyder
Balabol, balabolit, blah blah - etymologi Balabol som betyder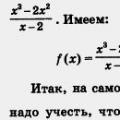 Bländare: vad är det och varför är det viktigt för en smartphone?
Bländare: vad är det och varför är det viktigt för en smartphone?