ما ریاضی را انتخاب نمی کنیمحرفه او، و او ما را انتخاب می کند.

ریاضیدان روسی Yu.I. مانین

معادلات مدولو

دشوارترین مسائل برای حل در ریاضیات مدرسه معادلات حاوی متغیرهای زیر علامت ماژول است. برای حل موفقیت آمیز چنین معادلاتی، لازم است که تعریف و ویژگی های اساسی ماژول را بدانید. طبیعتاً دانش آموزان باید مهارت حل معادلات از این نوع را داشته باشند.

مفاهیم و ویژگی های اساسی

مدول (مقدار مطلق) یک عدد واقعینشان داده شده است و به صورت زیر تعریف می شود:

ویژگی های ساده ماژول شامل روابط زیر است:

توجه داشته باشید، که دو خاصیت آخر برای هر درجه زوجی وجود دارد.

همچنین، اگر، کجا، سپس و

ویژگی های ماژول پیچیده تر, که می تواند به طور موثر در حل معادلات با ماژول ها استفاده شود, با استفاده از قضایای زیر فرموله می شوند:

قضیه 1.برای هر توابع تحلیلیو نابرابری

قضیه 2.برابری همان نابرابری است.

قضیه 3.برابری معادل نابرابری است.

نمونه های معمولی حل مسائل را در موضوع "معادلات" در نظر بگیرید, حاوی متغیرهایی در زیر علامت ماژول.

حل معادلات با مدول

رایج ترین روش در ریاضیات مدرسه برای حل معادلات با مدول روش است, بر اساس گسترش ماژول این روش عمومی است, با این حال، در مورد کلیاستفاده از آن می تواند به محاسبات بسیار دست و پا گیر منجر شود. در این راستا، دانش آموزان باید از موارد دیگر نیز آگاه باشند, بیشتر روش های موثرو روش های حل این گونه معادلات به خصوص, نیاز به داشتن مهارت برای اعمال قضایا, در این مقاله ارائه شده است.

مثال 1معادله را حل کنید. (یک)

راه حل. معادله (1) با روش "کلاسیک" - روش گسترش ماژول حل خواهد شد. برای این کار، محور عددی را می شکنیمنقطه و فواصل و سه مورد را در نظر بگیرید.

1. اگر , , , , و معادله (1) به شکل . از اینجا به دست می آید. با این حال، در اینجا، بنابراین مقدار یافت شده ریشه معادله (1) نیست.

2. اگر، سپس از رابطه (1) بدست می آوریمیا .

از آن به بعد ریشه معادله (1).

3. اگر، سپس معادله (1) شکل می گیردیا . توجه داشته باشید که.

پاسخ: ، .

هنگام حل معادلات زیر با یک ماژول، ما به طور فعال از خواص ماژول ها استفاده می کنیم تا کارایی حل این گونه معادلات را افزایش دهیم.

مثال 2معادله را حل کنید.

راه حل.از آنجایی که و سپس از معادله به دست می آید. در این رابطه، ، ، و معادله می شود. از اینجا می گیریم. ولی ، بنابراین معادله اصلی ریشه ندارد.

پاسخ: بدون ریشه.

مثال 3معادله را حل کنید.

راه حل.از آن به بعد . اگر پس از آن ، و معادله می شود.

از اینجا می گیریم.

مثال 4معادله را حل کنید.

راه حل.اجازه دهید معادله را به شکلی معادل بازنویسی کنیم. (2)

معادله به دست آمده متعلق به معادلات از نوع است.

با در نظر گرفتن قضیه 2، می توانیم بیان کنیم که معادله (2) معادل نابرابری است. از اینجا می گیریم.

پاسخ: .

مثال 5معادله را حل کنید.

راه حل. این معادله شکل دارد. بنابراین ، طبق قضیه 3, در اینجا ما نابرابری را داریمیا .

مثال 6معادله را حل کنید.

راه حل.بیایید آن را فرض کنیم. زیرا ، سپس معادله داده شده به شکل یک معادله درجه دوم در می آید, (3)

جایی که . از آنجایی که معادله (3) یک ریشه مثبت داردو سپس . از اینجا دو ریشه معادله اصلی را بدست می آوریم:و .

مثال 7 معادله را حل کنید. (4)

راه حل. از آنجایی که معادلهمعادل ترکیب دو معادله است:و پس در حل معادله (4) لازم است دو حالت در نظر گرفته شود.

1. اگر، پس یا .

از اینجا می گیریم و .

2. اگر، پس یا .

از آن به بعد .

پاسخ: ، ، ، .

مثال 8معادله را حل کنید . (5)

راه حل.از آن زمان و پس از آن . از اینجا و از معادله (5) نتیجه می شود که و، i.e. در اینجا ما یک سیستم معادلات داریم

با این حال، این سیستم معادلات ناسازگار است.

پاسخ: بدون ریشه.

مثال 9 معادله را حل کنید. (6)

راه حل.اگر تعیین کنیم و از رابطه (6) بدست می آوریم

یا . (7)

از آنجایی که معادله (7) دارای شکل است، این معادله معادل نامساوی است. از اینجا می گیریم. از آن پس یا .

پاسخ: .

مثال 10معادله را حل کنید. (8)

راه حل.طبق قضیه 1 می توانیم بنویسیم

(9)

با در نظر گرفتن رابطه (8)، نتیجه می گیریم که هر دو نابرابری (9) به برابری تبدیل می شوند، یعنی. یک سیستم معادلات وجود دارد

با این حال، با قضیه 3، سیستم معادلات فوق معادل سیستم نابرابری ها است.

(10)

با حل سیستم نابرابری ها (10) بدست می آوریم. از آنجایی که سیستم نابرابری ها (10) معادل معادله (8) است، معادله اصلی دارای یک ریشه است.

پاسخ: .

مثال 11. معادله را حل کنید. (11)

راه حل.اجازه دهید و سپس معادله (11) بر تساوی دلالت دارد.

از این نتیجه می شود که و . بنابراین، در اینجا ما یک سیستم نابرابری داریم

راه حل این سیستم از نابرابری ها هستندو .

پاسخ: ، .

مثال 12.معادله را حل کنید. (12)

راه حل. معادله (12) با روش بسط متوالی ماژول ها حل خواهد شد. برای این کار چند مورد را در نظر بگیرید.

1. اگر، پس.

1.1. اگر , پس و , .

1.2. اگر پس از آن . ولی ، بنابراین در این حالت معادله (12) ریشه ندارد.

2. اگر، پس.

2.1. اگر , پس و , .

2.2. اگر پس و .

پاسخ: ، ، ، ، .

مثال 13معادله را حل کنید. (13)

راه حل.از آنجایی که سمت چپ معادله (13) غیر منفی است، پس و . در این رابطه، و معادله (13)

شکل یا .

معلوم است که معادله معادل ترکیب دو معادله استو حل می کنیم که به دست می آوریم، . زیرا ، پس معادله (13) یک ریشه دارد.

پاسخ: .

مثال 14 حل یک سیستم معادلات (14)

راه حل.از زمان و پس از آن و . بنابراین از سیستم معادلات (14) چهار نظام معادله بدست می آید:

ریشه نظام های معادلات فوق ریشه نظام معادلات است (14).

پاسخ: ،، ، ، ، ، ، .

مثال 15 حل یک سیستم معادلات (15)

راه حل.از آن به بعد . در این راستا از سیستم معادلات (15) دو نظام معادله به دست می آید

ریشه های سیستم معادلات اول و و از سیستم معادلات دوم به دست می آید و .

پاسخ: ، ، ، .

مثال 16 حل یک سیستم معادلات (16)

راه حل.از معادله اول سیستم (16) چنین بر می آید که .

از آن به بعد . معادله دوم سیستم را در نظر بگیرید. تا جایی که، سپس ، و معادله می شود، ، یا .

اگر مقدار را جایگزین کنیمبه معادله اول سیستم (16)، سپس یا .

پاسخ: ، .

برای مطالعه عمیق تر روش های حل مسئله, مربوط به حل معادلات, حاوی متغیرهایی در زیر علامت ماژول, شما می توانید آموزش هایی را از لیست ادبیات توصیه شده راهنمایی کنید.

1. مجموعه تکالیف ریاضی برای متقاضیان دانشگاه های فنی / ویرایش. M.I. اسکانوی. - م .: جهان و آموزش، 2013. - 608 ص.

2. Suprun V.P. ریاضیات برای دانش آموزان دبیرستانی: وظایف با پیچیدگی افزایش یافته - M .: KD "Librocom" / URSS، 2017. - 200 ص.

3. Suprun V.P. ریاضیات برای دانش آموزان دبیرستانی: روش های غیر استاندارد برای حل مسائل. - M .: KD "Librocom" / URSS, 2017. - 296 ص.

آیا هیچ سوالی دارید؟

برای کمک گرفتن از یک معلم خصوصی - ثبت نام کنید.

سایت، با کپی کامل یا جزئی از مطالب، لینک به منبع الزامی است.

حل معادلات و نامساوی با مدولاغلب باعث ایجاد مشکلات می شود. با این حال، اگر خوب بفهمید چیست قدر مطلق یک عدد، و چگونه عبارات حاوی علامت مدول را به درستی گسترش دهیم، سپس حضور در معادله عبارت زیر علامت ماژولمانعی بر سر راه حل آن نمی شود.

کمی تئوری هر عدد دو ویژگی دارد: قدر مطلق عدد و علامت آن.

به عنوان مثال، عدد +5 یا فقط 5 دارای علامت "+" و قدر مطلق 5 است.

عدد -5 دارای علامت "-" و قدر مطلق 5 است.

قدر مطلق اعداد 5 و -5 5 است.

قدر مطلق عدد x را مدول عدد می نامند و با |x| نشان می دهند.

همانطور که می بینیم مدول یک عدد در صورتی که این عدد بزرگتر یا مساوی صفر باشد با خود عدد و اگر این عدد منفی باشد با این عدد با علامت مخالف برابر است.

همین امر در مورد هر عبارتی که در زیر علامت ماژول قرار دارد صدق می کند.

قانون گسترش ماژول به شکل زیر است:

|f(x)|= f(x) اگر f(x) ≥ 0، و

|f(x)|= - f(x) اگر f(x)< 0

برای مثال |x-3|=x-3 اگر x-3≥0 و |x-3|=-(x-3)=3-x اگر x-3<0.

برای حل یک معادله حاوی عبارت زیر علامت مدول، ابتدا باید گسترش ماژول توسط قانون گسترش ماژول.

سپس معادله یا نابرابری ما تبدیل می شود به دو معادله متفاوت که در دو بازه عددی متفاوت وجود دارد.

یک معادله در یک بازه عددی وجود دارد که در آن عبارت زیر علامت مدول غیر منفی است.

و معادله دوم در فاصله ای وجود دارد که عبارت زیر علامت مدول منفی است.

بیایید یک مثال ساده را در نظر بگیریم.

بیایید معادله را حل کنیم:

|x-3|=-x 2 +4x-3

1. بیایید ماژول را باز کنیم.

|x-3|=x-3 اگر x-3≥0، یعنی. اگر x≥3

|x-3|=-(x-3)=3-x اگر x-3<0, т.е. если х<3

2. دو بازه عددی بدست آوردیم: x≥3 و x<3.

در نظر بگیرید که معادله اصلی در هر بازه به چه معادلاتی تبدیل می شود:

الف) برای x≥3 |x-3|=x-3، و معادله ما به نظر می رسد:

توجه! این معادله فقط در بازه x≥3 وجود دارد!

بیایید پرانتزها را باز کنیم، اعضای مشابه بدهیم:

و این معادله را حل کنید.

این معادله ریشه دارد:

x 1 \u003d 0، x 2 \u003d 3

توجه! از آنجایی که معادله x-3=-x 2 +4x-3 فقط در بازه x≥3 وجود دارد، ما فقط به ریشه هایی علاقه مندیم که به این بازه تعلق دارند. این شرط فقط x 2 = 3 را برآورده می کند.

ب) در x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

توجه! این معادله فقط در بازه x وجود دارد<3!

بیایید پرانتزها را باز کنیم و اصطلاحات مشابه را بیان کنیم. معادله را بدست می آوریم:

x 1 \u003d 2، x 2 \u003d 3

توجه! از آنجایی که معادله 3-x \u003d -x 2 + 4x-3 فقط در بازه x وجود دارد<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

بنابراین: از فاصله اول فقط ریشه x=3 را می گیریم، از دومی - ریشه x=2.

در میان نمونه در هر ماژولاغلب معادلاتی وجود دارد که باید آنها را پیدا کنید ریشه های ماژول در ماژول، یعنی معادله ای از فرم
||a*x-b|-c|=k*x+m .
اگر k=0، یعنی سمت راست برابر با یک ثابت (m) باشد، راحت تر به دنبال راه حل می گردیم. معادلات با ماژول ها به صورت گرافیکیدر زیر روش شناسی آمده است استقرار ماژول های دوتاییدر نمونه های عملی رایج الگوریتم محاسبه معادلات با ماژول ها را به خوبی درک کنید تا در کنترل، تست ها و فقط دانستن مشکل نداشته باشید.

مثال 1 حل ماژول معادله در ماژول |3|x|-5|=-2x-2.
راه حل: همیشه گسترش معادلات را از ماژول داخلی شروع کنید
|x|=0 <->x=0.
در نقطه x=0 معادله مدول بر 2 تقسیم می شود.
برای x< 0 подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
برای x> 0 یا مساوی، با گسترش مدول ما
|3x-5|=-2x-2 .
بیایید معادله را حل کنیمبرای متغیرهای منفی (x< 0) . Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе - раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная - меняем знак правой или левой части (зависит от методики преподавания).

از معادله اول، دریافت می کنیم که راه حل نباید از (-1) تجاوز کند، یعنی.

این محدودیت کاملاً متعلق به حوزه ای است که ما در آن حل می کنیم. بیایید متغیرها و ثابت ها را در دو طرف برابری در سیستم اول و دوم حرکت دهیم

و راه حلی پیدا کنید


هر دو مقدار متعلق به فاصله ای است که در نظر گرفته می شود، یعنی ریشه هستند.
معادله ای با ماژول برای متغیرهای مثبت در نظر بگیرید
|3x-5|=-2x-2.
با گسترش ماژول، دو سیستم معادله به دست می آوریم

از معادله اول که برای دو سیستم مشترک است، شرط آشنا را به دست می آوریم

که در تقاطع با مجموعه ای که در آن به دنبال راه حل هستیم، یک مجموعه خالی (بدون نقطه تقاطع) می دهد. بنابراین تنها ریشه های ماژول با ماژول مقادیر هستند
x=-3; x=-1.4.

مثال 2 معادله را با مدول حل کنید ||x-1|-2|=3x-4.
راه حل: بیایید با گسترش ماژول داخلی شروع کنیم
|x-1|=0 <=>x=1.
یک تابع زیر ماژول علامت را در یک تغییر می دهد. در مقادیر کوچکتر منفی و در مقادیر بزرگتر مثبت است. مطابق با این، هنگام گسترش ماژول داخلی، دو معادله با ماژول به دست می آوریم
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
حتما سمت راست معادله را با مدول بررسی کنید، باید بزرگتر از صفر باشد.
3x-4>=0 -> x>=4/3.
این بدان معنی است که نیازی به حل معادلات اول نیست، زیرا برای x نوشته شده است< 1, что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4یا x-3=4-3x;
4-3=3x-x یا x+3x=4+3;
2x=1 یا 4x=7;
x=1/2 یا x=7/4.
ما دو مقدار گرفتیم که اولی رد می شود، زیرا به بازه مورد نظر تعلق ندارد. معادله نهایی یک جواب x=7/4 دارد.

مثال 3 معادله را با مدول ||2x-5|-1|=x+3 حل کنید.
راه حل: بیایید ماژول داخلی را باز کنیم
|2x-5|=0 <=>x=5/2=2.5.
نقطه x=2.5 محور عددی را به دو بازه تقسیم می کند. به ترتیب، تابع زیر ماژولهنگام عبور از 2.5 علامت تغییر می کند. اجازه دهید شرط را روی جواب سمت راست معادله با مدول بنویسیم.
x+3>=0 -> x>=-3.
بنابراین راه حل می تواند مقادیر کمتر از (-3) نباشد. بیایید مدول را برای مقدار منفی مدول داخلی گسترش دهیم
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
این ماژول همچنین پس از گسترش، 2 معادله به دست می دهد
-2x+4=x+3 یا 2x-4=x+3.
2x+x=4-3 یا 2x-x=3+4;
3x=1; x=1/3 یا x=7.
مقدار x=7 رد می شود، زیرا ما به دنبال راه حلی در بازه [-3;2.5] بودیم. اکنون ماژول داخلی را برای x>2.5 گسترش دهید. با یک ماژول معادله ای بدست می آوریم
|2x-5-1|=x+3;
|2x-6|=x+3.
هنگام گسترش ماژول، معادلات خطی زیر را به دست می آوریم
-2x+6=x+3 یا 2x-6=x+3.
2x+x=6-3 یا 2x-x=3+6;
3x=3; x=1 یا x=9.
مقدار اول x=1 شرط x>2.5 را برآورده نمی کند. بنابراین در این بازه یک ریشه معادله با ماژول x=9 داریم و فقط دو تا از آنها وجود دارد (x=1/3) با جایگزینی می توانید صحت محاسبات انجام شده را بررسی کنید.
پاسخ: x=1/3; x=9.

مثال 4 راه حل های ماژول دوگانه را پیدا کنید ||3x-1|-5|=2x-3.
راه حل: ماژول داخلی معادله را گسترش دهید
|3x-1|=0 <=>x=1/3.
نقطه x=2.5 محور عددی را به دو بازه و معادله داده شده را به دو حالت تقسیم می کند. شرط حل را بر اساس نوع معادله سمت راست می نویسیم
2x-3>=0 -> x>=3/2=1.5.
نتیجه این است که ما به مقادیر>=1.5 علاقه مند هستیم. به این ترتیب معادله مدولاربه دو بازه نگاه کنید
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
ماژول حاصل، هنگامی که گسترش می یابد، به 2 معادله تقسیم می شود
-3x-4=2x-3 یا 3x+4=2x-3.
2x+3x=-4+3 یا 3x-2x=-3-4;
5x=-1; x=-1/5 یا x=-7.
هر دو مقدار در فاصله زمانی قرار نمی گیرند، یعنی راه حلی برای معادله با ماژول ها نیستند. بعد، مدول را برای x>2.5 گسترش دهید. معادله زیر را بدست می آوریم
|3x-1-5|=2x-3;
|3x-6|=2x-3.
با گسترش ماژول، 2 معادله خطی به دست می آوریم
3x-6=2x-3 یا –(3x-6)=2x-3;
3x-2x=-3+6یا 2x+3x=6+3;
x=3 یا 5x=9; x=9/5=1.8.
مقدار دوم یافت شده شرط x>2.5 را ندارد، ما آن را رد می کنیم.
در نهایت یک ریشه معادله با ماژول های x=3 داریم.
ما یک بررسی انجام می دهیم
||3*3-1|-5|=2*3-3 3=3 .
ریشه معادله با مدول به درستی محاسبه شده است.
پاسخ: x=1/3; x=9.

این ماشین حساب ریاضیآنلاین به شما کمک کند معادله یا نابرابری را با ماژول حل کنید. برنامه برای حل معادلات و نابرابری ها با ماژول هانه تنها پاسخ مشکل را می دهد، بلکه منجر می شود راه حل دقیق با توضیحات، یعنی روند به دست آوردن نتیجه را نمایش می دهد.

این برنامه می تواند برای دانش آموزان دبیرستانی در آماده سازی مفید باشد کار کنترلو امتحانات، هنگام تست دانش قبل از امتحان، والدین برای کنترل حل بسیاری از مسائل در ریاضیات و جبر. یا شاید استخدام معلم خصوصی یا خرید کتاب های درسی جدید برای شما گران باشد؟ یا فقط می خواهید آن را در اسرع وقت انجام دهید؟ مشق شبریاضی یا جبر؟ در این مورد، شما همچنین می توانید از برنامه های ما با یک راه حل دقیق استفاده کنید.

به این ترتیب، شما می توانید آموزش و/یا آموزش خود را انجام دهید برادران کوچکتریا خواهران، در حالی که سطح تحصیلات در زمینه کارهای در حال حل افزایش می یابد.

|x| یا abs(x) - ماژول x

معادله یا نابرابری را با مدول وارد کنید

معادله یا نابرابری را حل کنید

مشخص شد که برخی از اسکریپت های مورد نیاز برای حل این کار بارگیری نمی شوند و ممکن است برنامه کار نکند.
ممکن است AdBlock را فعال کرده باشید.
در این صورت آن را غیرفعال کرده و صفحه را Refresh کنید.

شما جاوا اسکریپت را در مرورگر خود غیرفعال کرده اید.
جاوا اسکریپت باید فعال باشد تا راه حل ظاهر شود.
در اینجا دستورالعمل هایی در مورد نحوه فعال کردن جاوا اسکریپت در مرورگر خود آورده شده است.

زیرا افراد زیادی هستند که می خواهند مشکل را حل کنند، درخواست شما در صف است.
پس از چند ثانیه، راه حل در زیر ظاهر می شود.
لطفا صبر کنید ثانیه...

اگر شما متوجه خطا در راه حل شد، سپس می توانید در مورد آن در فرم بازخورد بنویسید.
فراموش نکن مشخص کنید کدام کارشما تصمیم می گیرید چه چیزی در فیلدها وارد کنید.

بازی ها، پازل ها، شبیه سازهای ما:

کمی تئوری

معادلات و نابرابری ها با ماژول ها

در درس جبر مدرسه ابتدایی می توانید ساده ترین معادلات و نابرابری ها را با ماژول ها برآورده کنید. برای حل آنها می توانید یک روش هندسی بر اساس این واقعیت اعمال کنید که \(|xa| \) فاصله روی خط عددی بین نقاط x و a است: \(|xa| = \rho (x;\; a ) \). به عنوان مثال، برای حل معادله \(|x-3|=2 \)، باید نقاطی را در خط عددی پیدا کنید که در فاصله 2 از نقطه 3 قرار دارند. دو نقطه از این قبیل وجود دارد: \(x_1=1 \) و \(x_2=5 \) .

حل نابرابری \(|2x+7|

اما راه اصلی برای حل معادلات و نابرابری ها با ماژول ها مربوط به به اصطلاح "بسط ماژول بر اساس تعریف" است:
اگر \(a \geq 0 \)، سپس \(|a|=a \);
if \(a به عنوان یک قاعده، یک معادله (نابرابری) با ماژول ها به مجموعه ای از معادلات (نابرابری) کاهش می یابد که شامل علامت ماژول نیست.

علاوه بر تعریف فوق، از ادعاهای زیر استفاده می شود:
1) اگر \(c > 0 \)، معادله \(|f(x)|=c \) معادل مجموعه معادلات است: \(\left[\begin(array)(l) f(x )=c \\ f(x)=-c \end(آرایه)\راست.\)
2) اگر \(c > 0 \)، پس نابرابری \(|f(x)| 3) اگر \(c \geq 0 \)، آنگاه نابرابری \(|f(x)| > c \) برابر است با معادل مجموعه نابرابری ها: \(\left[\begin(array)(l) f(x) c \end(array)\right. \)
4) اگر هر دو طرف نابرابری \(f(x) مثال 1. معادله \(x^2 +2|x-1| -6 = 0 \) را حل کنید.

اگر \(x-1 \geq 0 \)، آنگاه \(|x-1| = x-1 \) و معادله داده شده تبدیل می شود
\(x^2 +2(x-1) -6 = 0 \پیکان راست x^2 +2x -8 = 0 \).
اگر \(x-1 \(x^2 -2(x-1) -6 = 0 \راست فلش x^2 -2x -4 = 0 \).
بنابراین، معادله داده شده باید به طور جداگانه در هر یک از دو مورد اشاره شده در نظر گرفته شود.
1) اجازه دهید \(x-1 \geq 0 \)، یعنی. \(x \geq 1 \). از معادله \(x^2 +2x -8 = 0 \) \(x_1=2, \; x_2=-4\) را پیدا می کنیم. شرط \(x \geq 1 \) فقط با مقدار \(x_1=2\) ارضا می شود.
2) اجازه دهید \(x-1 پاسخ دهد: \(2; \;\; 1-\sqrt(5) \)

مثال 2. معادله \(|x^2-6x+7| = \frac(5x-9)(3) \) را حل کنید.

راه اول(توسعه ماژول بر اساس تعریف).
با استدلال مانند مثال 1، نتیجه می گیریم که معادله داده شده باید به طور جداگانه تحت دو شرط در نظر گرفته شود: \(x^2-6x+7 \geq 0 \) یا \(x^2-6x+7

1) اگر \(x^2-6x+7 \geq 0 \)، آنگاه \(|x^2-6x+7| = x^2-6x+7 \) و معادله داده شده می شود \(x^2 -6x+7 = \frac(5x-9)(3) \Rightarrow 3x^2-23x+30=0 \). حل کردن آن معادله درجه دوم، دریافت می کنیم: \(x_1=6, \; x_2=\frac(5)(3) \).
بیایید دریابیم که آیا مقدار \(x_1=6 \) شرط \(x^2-6x+7 \geq 0 \) را برآورده می کند یا خیر. برای این ما جایگزین می کنیم مقدار مشخص شدهبه یک نابرابری درجه دوم. دریافت می کنیم: \(6^2-6 \cdot 6+7 \geq 0 \)، یعنی. \(7 \geq 0 \) نابرابری صحیح است. بنابراین، \(x_1=6 \) ریشه معادله داده شده است.
بیایید دریابیم که آیا مقدار \(x_2=\frac(5)(3) \) شرط \(x^2-6x+7 \geq 0 \) را برآورده می کند یا خیر. برای انجام این کار، مقدار مشخص شده را با نابرابری درجه دوم جایگزین می کنیم. دریافت می کنیم: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \)، یعنی. \(\frac(25)(9) -3 \geq 0 \) یک نابرابری نامعتبر است. بنابراین \(x_2=\frac(5)(3) \) ریشه معادله داده شده نیست.

2) اگر \(x^2-6x+7 مقدار \(x_3=3\) شرط \(x^2-6x+7 را برآورده کند مقدار \(x_4=\frac(4)(3) \) شرط \ را برآورده نمی کند (x^2-6x+7 بنابراین، معادله داده شده دو ریشه دارد: \(x=6, \; x=3 \).

راه دوم.با توجه به یک معادله \(|f(x)| = h(x) \)، سپس برای \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(آرایه)\راست. \)
هر دوی این معادلات در بالا حل شده اند (با روش اول برای حل معادله داده شده)، ریشه آنها به شرح زیر است: \(6,\; \frac(5)(3),\; 3,\; \frac(4) ) (3) \). شرط \(\frac(5x-9)(3) \geq 0 \) از این چهار مقدار فقط با دو عدد: 6 و 3 ارضا می شود. بنابراین، معادله داده شده دارای دو ریشه است: \(x=6، \; x=3 \ ).

راه سوم(گرافیک).
1) بیایید تابع \(y = |x^2-6x+7| \) را رسم کنیم. ابتدا یک سهمی \(y = x^2-6x+7\) می سازیم. ما \(x^2-6x+7 = (x-3)^2-2 \) داریم. نمودار تابع \(y = (x-3)^2-2 \) را می توان از نمودار تابع \(y = x^2 \) با جابجایی 3 واحد مقیاس به سمت راست (در سمت راست) بدست آورد. محور x) و 2 واحد مقیاس پایین (در امتداد محور y). خط راست x=3 محور سهمی است که ما به آن علاقه داریم. به عنوان نقاط کنترل برای ترسیم دقیق تر، گرفتن نقطه (3؛ -2) - بالای سهمی، نقطه (0؛ 7) و نقطه (6؛ 7) متقارن با آن نسبت به محور راحت است. سهمی
اکنون برای ساختن نمودار تابع \(y = |x^2-6x+7| \)، باید قسمت هایی از سهمی ساخته شده را که زیر محور x قرار ندارند، بدون تغییر رها کنید و بخشی از آن را منعکس کنید. سهمی که زیر محور x حول محور x قرار دارد.
2) بیایید یک نمودار بسازیم تابع خطی\(y = \frac(5x-9)(3) \). گرفتن نقاط (0; -3) و (3; 2) به عنوان نقاط کنترل راحت است.

ضروری است که نقطه x \u003d 1.8 از تقاطع خط مستقیم با محور آبسیسا در سمت راست نقطه تقاطع چپ سهمی با محور آبسیسا قرار گیرد - این نقطه \(x=3-\ است. sqrt(2) \) (از آنجا که \(3-\sqrt(2) 3) با قضاوت در نقاشی، نمودارها در دو نقطه - A (3; 2) و B (6; 7) قطع می شوند. نقاط x \u003d 3 و x \u003d 6 در معادله داده شده، مطمئن می شویم که هر دو مقدار دیگر برابری عددی صحیح را ارائه می دهند. بنابراین، فرضیه ما تأیید شد - معادله دو ریشه دارد: x \u003d 3 و x \u003d 6 پاسخ: 3؛ 6.

اظهار نظر. روش گرافیکی، با همه ظرافت آن، چندان قابل اعتماد نیست. در مثال در نظر گرفته شده، فقط به این دلیل کار می کند که ریشه های معادله اعداد صحیح هستند.

مثال 3. حل معادله \(|2x-4|+|x+3| = 8 \)

راه اول
عبارت 2x–4 در نقطه x = 2 0 و عبارت x + 3 در نقطه x = –3 می شود. این دو نقطه خط اعداد را به سه بازه تقسیم می کنند: \(x

اولین فاصله را در نظر بگیرید: \((-\infty; \; -3) \).
اگر x بازه دوم را در نظر بگیرید: \([-3; \; 2) \).
اگر \(-3 \leq x بازه سوم را در نظر بگیرید: \( پاسخ: طول شکاف 6 است.№3 . معادله را حل کنید، در پاسخ تعداد جواب های عدد صحیح را نشان دهید: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] پاسخ: 4 راه حل کامل.№4 . معادله را حل کنید، در پاسخ بزرگترین ریشه را مشخص کنید:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1.2 \u003d
≈ 1,4

پاسخ: x = 3.

تمرینات: №12. معادله را حل کنید، در پاسخ تمام ریشه را نشان دهید: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. معادله را حل کنید، در پاسخ تعداد جواب های عدد صحیح را نشان دهید: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. معادله را حل کنید، در پاسخ یک عدد صحیح را مشخص کنید که ریشه معادله نیست:

بخش 5. معادلات شکل │F(x)│= │G(x)│

از آنجایی که هر دو طرف معادله غیر منفی هستند، راه حل شامل در نظر گرفتن دو حالت است: عبارات زیرماژول مساوی یا مخالف علامت هستند. بنابراین، معادله اصلی معادل ترکیب دو معادله است: │ اف(ایکس)│= │ جی(ایکس)│
مثال ها: №1. معادله را حل کنید، در پاسخ کل ریشه را نشان دهید: │x + 3│ \u003d │2x - 1│
پاسخ: ریشه عدد صحیح x = 4.№2. معادله را حل کنید: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
پاسخ: x = 2.№3 . معادله را حل کنید، در جواب حاصل ضرب ریشه ها را مشخص کنید:




ریشه های معادله 4x 2 + 2x - 1 \u003d 0 x 1.2 \u003d - 1±√5 / 4 پاسخ: حاصل ضرب ریشه ها 0.25 است. تمرینات: №15 . معادله را حل کنید، در پاسخ کل راه حل را نشان دهید: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. معادله را حل کنید، در پاسخ ریشه کوچکتر را نشان دهید: │5x - 3│=│7 - x│ №17 . معادله را حل کنید، در جواب مجموع ریشه ها را بنویسید:

بخش 6. نمونه هایی از حل معادلات غیر استاندارد

در این بخش نمونه هایی از معادلات غیر استاندارد را در نظر می گیریم که در حل آنها قدر مطلق عبارت با تعریف آشکار می شود. مثال ها:

№1. معادله را حل کنید، در پاسخ مجموع ریشه ها را مشخص کنید: x │x│- 5x - 6 \u003d 0
پاسخ: مجموع ریشه ها 1 است №2. . معادله را حل کنید، در پاسخ ریشه کوچکتر را نشان دهید: x 2 - 4x
- 5 = 0
پاسخ: ریشه کوچکتر x = - 5. №3. معادله را حل کنید:

پاسخ: x = -1. تمرینات: №18. معادله را حل کنید و مجموع ریشه ها را بنویسید: x │3x + 5│= 3x 2 + 4x + 3
№19. معادله را حل کنید: x 2 - 3x \u003d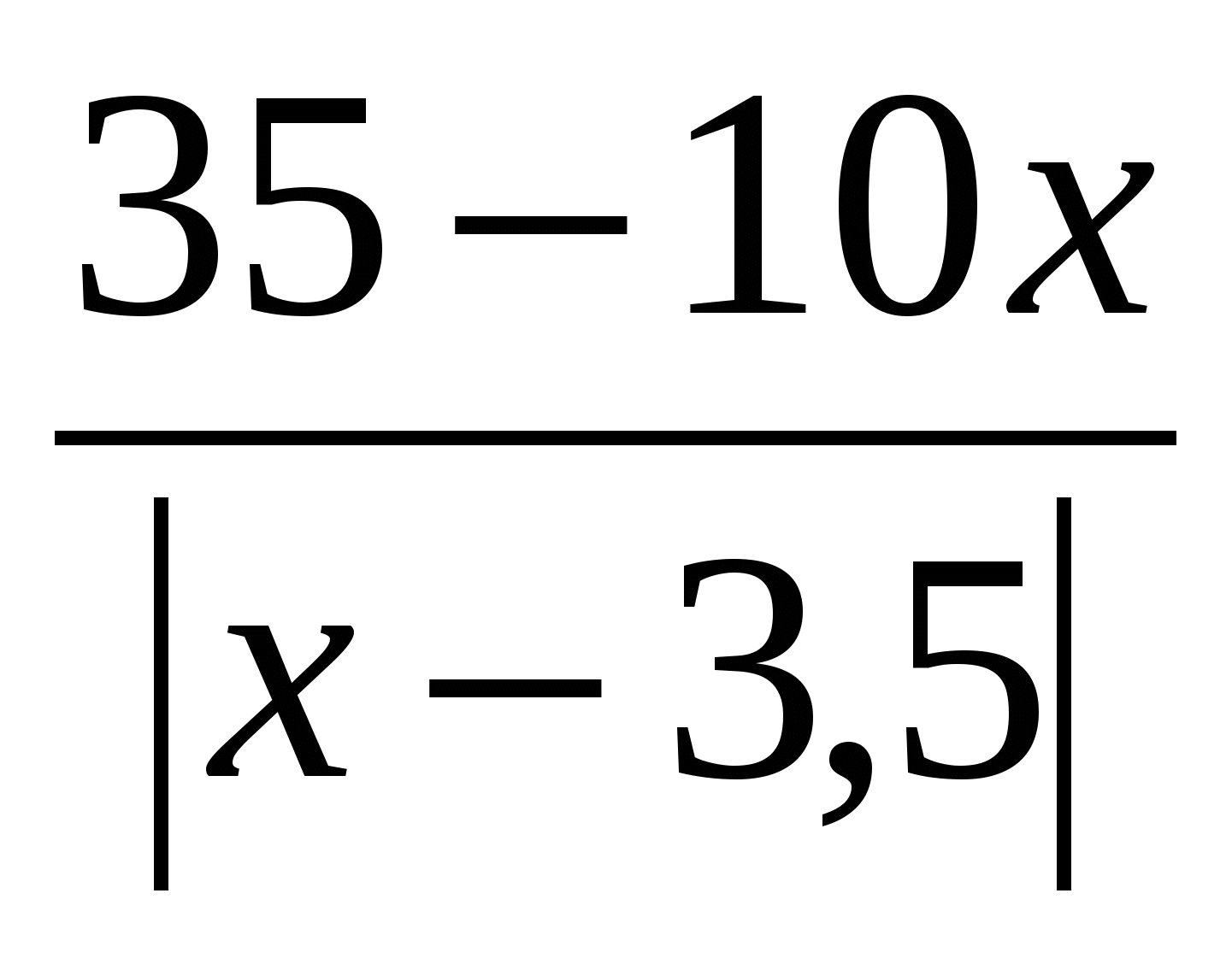

№20. معادله را حل کنید:

بخش 7. معادلات شکل │F(x)│+│G(x)│=0

به راحتی می توان دید که در سمت چپ معادله ای از این نوع، مجموع مقادیر غیر منفی است. بنابراین، معادله اصلی یک راه حل دارد اگر و تنها در صورتی که هر دو عبارت به طور همزمان برابر با صفر باشند. معادله معادل سیستم معادلات است: │ اف(ایکس)│+│ جی(ایکس)│=0
مثال ها: №1 . معادله را حل کنید:
پاسخ: x = 2. №2. معادله را حل کنید: پاسخ: x = 1. تمرینات: №21. معادله را حل کنید: №22 . معادله را حل کنید، در جواب مجموع ریشه ها را بنویسید: №23 . معادله را حل کنید، در پاسخ تعداد جواب ها را مشخص کنید:

بخش 8. معادلات فرم

برای حل معادلات از این نوع از روش فواصل استفاده می شود. اگر با گسترش متوالی ماژول ها حل شود، به دست می آوریم nمجموعه ای از سیستم ها، که بسیار دست و پا گیر و ناخوشایند است. الگوریتم روش بازه ای را در نظر بگیرید: 1). مقادیر متغیر را پیدا کنید ایکس، که برای آن هر ماژول برابر با صفر است (صفر عبارات زیر ماژول):
2). مقادیر یافت شده روی یک خط عددی مشخص شده اند که به فواصل تقسیم می شود (تعداد بازه ها به ترتیب برابر است با n+1 ) 3). تعیین کنید که هر ماژول در هر یک از فواصل به دست آمده با چه علامتی نشان داده می شود (هنگام ایجاد راه حل، می توانید از یک خط عددی استفاده کنید و علائم را روی آن علامت گذاری کنید) 4). معادله اصلی معادل مجموعه است n+1 سیستم هایی که در هر یک از آنها عضویت متغیر مشخص شده است ایکسیکی از فواصل مثال ها: №1 . معادله را حل کنید، در پاسخ بزرگترین ریشه را مشخص کنید:
یک). بیایید صفر عبارات زیر ماژول را پیدا کنیم: x = 2; x = -3 2). مقادیر یافت شده را روی خط شماره علامت گذاری می کنیم و مشخص می کنیم که هر ماژول در فواصل به دست آمده با چه علامتی نشان داده می شود:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- هیچ راه حلی معادله دو ریشه دارد. پاسخ: بزرگترین ریشه x=2 است. №2. معادله را حل کنید، تمام ریشه را در پاسخ بنویسید:
یک). بیایید صفر عبارات زیر ماژول را پیدا کنیم: x = 1.5; x = - 1 2). مقادیر یافت شده را روی خط شماره علامت گذاری می کنیم و مشخص می کنیم که هر ماژول با چه علامتی در فواصل به دست آمده نشان داده می شود: x + 1 x + 1 x + 1 - + +
-1 1.5 x 2x – 3 2x – 3 2x – 3 - - +
3).
سیستم آخر هیچ راه حلی ندارد، بنابراین معادله دو ریشه دارد. هنگام حل معادله باید به علامت "-" در جلوی ماژول دوم توجه کنید. پاسخ: ریشه عدد صحیح x = 7. №3. معادله را حل کنید، در جواب مجموع ریشه ها را مشخص کنید: 1). بیایید صفر عبارات زیر ماژول را پیدا کنیم: x = 5; x = 1; x = - 2 2). مقادیر یافت شده را روی خط شماره علامت گذاری می کنیم و مشخص می کنیم که هر ماژول با چه علامتی در فواصل به دست آمده نشان داده می شود: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
معادله دو ریشه x = 0 و 2 دارد. پاسخ: مجموع ریشه ها 2 است. №4 . معادله را حل کنید: 1). بیایید صفر عبارات زیر ماژول را پیدا کنیم: x = 1; x = 2; x = 3. 2). اجازه دهید علامتی را تعیین کنیم که با آن هر ماژول در فواصل به دست آمده گسترش می یابد. 3).
بیایید راه حل های اول را با هم ترکیب کنیم سه سیستم. پاسخ: ؛ x = 5.
تمرینات: №24. معادله را حل کنید:
№25. معادله را حل کنید، در جواب مجموع ریشه ها را بنویسید: №26. معادله را حل کنید، در پاسخ ریشه کوچکتر را مشخص کنید: №27. معادله را حل کنید، در پاسخ خود ریشه بزرگتر بدهید:

بخش 9. معادلات حاوی چند ماژول

معادلات حاوی چندین ماژول وجود مقادیر مطلق را در عبارات زیر ماژول فرض می کنند. اصل اساسی حل معادلات از این نوع، افشای متوالی ماژول ها است که با "خارجی" شروع می شود. در مسیر حل، از تکنیک های بحث شده در بخش های شماره 1، شماره 3 استفاده می شود.

مثال ها: №1. معادله را حل کنید:
پاسخ: x = 1; - یازده №2. معادله را حل کنید:
پاسخ: x = 0; 4 - 4. №3. معادله را حل کنید، در جواب حاصل ضرب ریشه ها را مشخص کنید:
جواب: حاصلضرب ریشه 8 است. №4. معادله را حل کنید:
معادلات جمعیت را نشان دهید (1) و (2) و برای راحتی طراحی راه حل هر کدام را جداگانه در نظر بگیرید. از آنجایی که هر دو معادله حاوی بیش از یک ماژول هستند، انجام یک انتقال معادل به مجموعه‌ای از سیستم‌ها راحت‌تر است. (1)

(2)


پاسخ:
تمرینات: №36. معادله را حل کنید، در پاسخ مجموع ریشه ها را مشخص کنید: 5 │3x-5│ \u003d 25 x №37. معادله را حل کنید، اگر بیش از یک ریشه وجود دارد، در پاسخ مجموع ریشه ها را مشخص کنید: │x + 2│ x - 3x - 10 = 1 №38. معادله را حل کنید: 3│2x -4│ \u003d 9│x│ №39. معادله را حل کنید، در پاسخ تعداد ریشه ها را مشخص کنید: 2 │ sin x │ = √2 №40 . معادله را حل کنید، در پاسخ تعداد ریشه ها را مشخص کنید:

بخش 3. معادلات لگاریتمی.

قبل از حل معادلات زیر لازم است خصوصیات لگاریتم و تابع لگاریتمی بررسی شود. مثال ها: №1. معادله را حل کنید، در پاسخ حاصل ضرب ریشه ها را مشخص کنید: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

مورد 1: اگر x ≥ - 1، سپس log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 - شرایط x ≥ - 1 2 را برآورده می کند: اگر x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – شرایط x - 1 را برآورده می کند
جواب: حاصلضرب ریشه 15 است.
№2. معادله را حل کنید، در جواب مجموع ریشه ها را مشخص کنید: lg
O.D.Z.

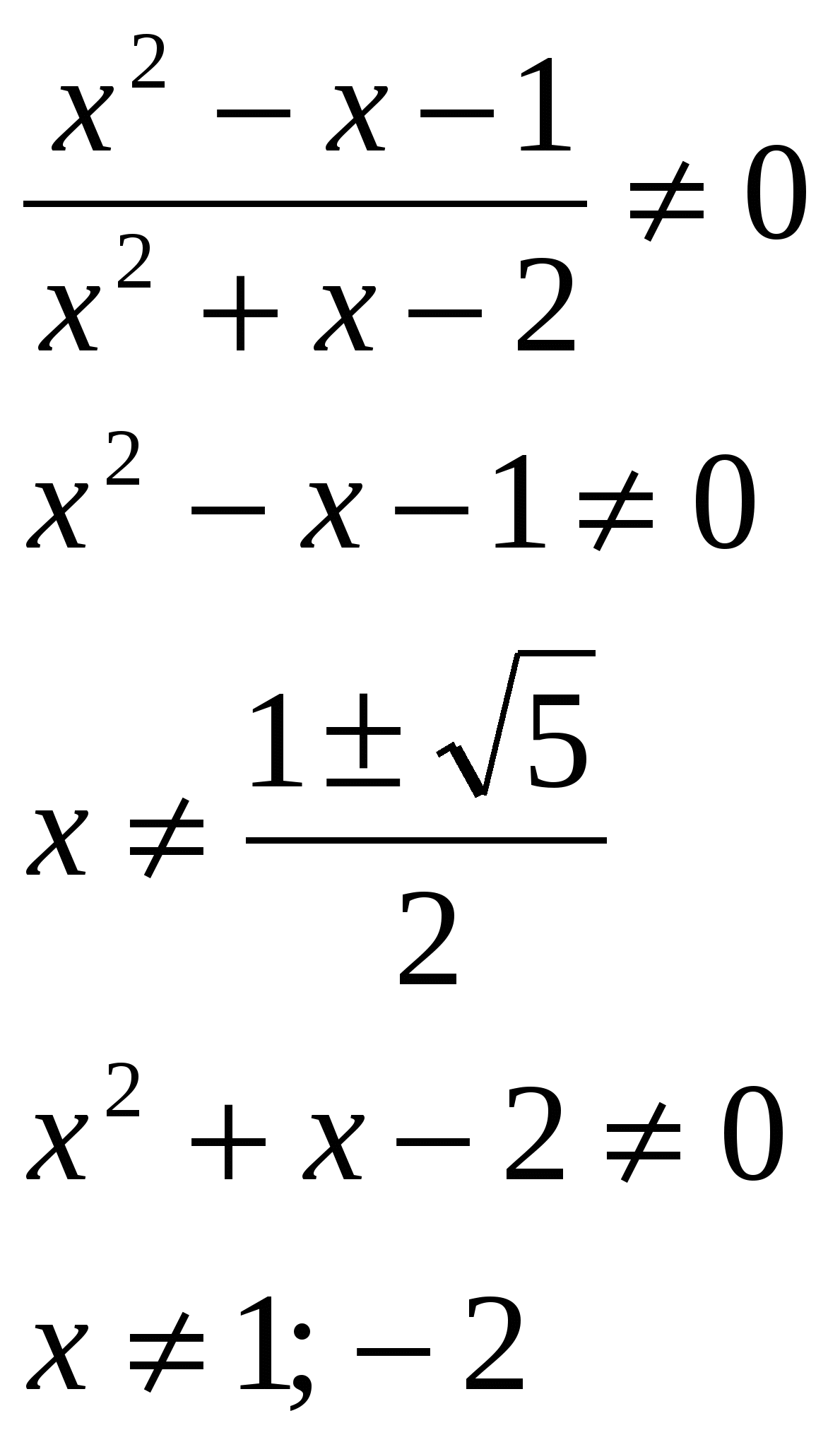
پاسخ: مجموع ریشه ها 0.5 است.
№3. معادله log 5 را حل کنید
O.D.Z.

پاسخ: x = 9. №4. معادله را حل کنید: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 بیایید از فرمول انتقال به پایه دیگر استفاده کنیم. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 بیایید صفرهای عبارات زیرماژول را پیدا کنیم: x = 25; x \u003d این اعداد مساحت مقادیر مجاز را به سه بازه تقسیم می کنند، بنابراین معادله معادل مجموع سه سیستم است.
پاسخ: )