Trigonometric equations of the reduction formula. How Cast Formulas Work in Problem B11
Lesson topic
- Change in sine, cosine and tangent with increasing angle.
Lesson objectives
- Get acquainted with new definitions and recall some already studied.
- Get acquainted with the regularity of changes in the values of the sine of the cosine and the tangent with increasing angle.
- Developing - to develop students' attention, perseverance, perseverance, logical thinking, mathematical speech.
- Educational - through the lesson to bring up an attentive attitude to each other, instill the ability to listen to comrades, mutual assistance, independence.
Lesson Objectives
- Check student knowledge.
Lesson plan
- Repetition of previously studied material.
- Repetition tasks.
- Change in sine, cosine and tangent with increasing angle.
- Practical use.
Repetition of previously learned material
Let's start from the very beginning and remember what will be useful to refresh your memory. What are sine, cosine and tangent and which section of geometry these concepts relate to?
Trigonometry is such a complex Greek word: trigon is a triangle, metro is to measure. So in Greek it means: measured by triangles.
Subjects> Mathematics> Grade 8 MathematicsHow to remember the formulas for the reduction of trigonometric functions? It's easy if you use an association; this association was not invented by me. As already mentioned, a good association should "catch", that is, evoke vivid emotions. I cannot call the emotions caused by this association positive. But it gives the result - it allows you to memorize the reduction formulas, which means it has the right to exist. After all, if you don't like it, you don't have to use it, right?
The reduction formulas are: sin (πn / 2 ± α), cos (πn / 2 ± α), tan (πn / 2 ± α), ctg (πn / 2 ± α). We remember that + α gives counterclockwise movement, - α - clockwise movement.
To work with reduction formulas, two points are needed:
1) we put the sign that the initial function has (in textbooks they write: reducible. But, in order not to get confused, it is better to call it initial), if α is considered an angle of the I quarter, that is, small.
2) Horizontal diameter - π ± α, 2π ± α, 3π ± α… - in general, when there is no fraction - the name of the function does not change. Vertical π / 2 ± α, 3π / 2 ± α, 5π / 2 ± α… - when there is a fraction, the function name changes: sine - to cosine, cosine - to sine, tangent - to cotangent and cotangent - to tangent. 
Now, in fact, the association:
vertical diameter (there is a fraction) -
drunk stands. What will happen to him early
or is it late? That's right, it will fall.
The function name will change.
If the diameter is horizontal, the drunk is already lying. Asleep, I guess. Nothing will happen to him, he has already taken a horizontal position. Accordingly, the name of the function does not change.

That is, sin (π / 2 ± α), sin (3π / 2 ± α), sin (5π / 2 ± α), etc. give ± cosα,
and sin (π ± α), sin (2π ± α), sin (3π ± α),… - ± sinα.
As we already know.
How it works? Let's look at examples.
1) cos (π / 2 + α) =?
We stand at π / 2. Since + α means we go forward, counterclockwise. We find ourselves in the second quarter, where the cosine has a “-“ sign. The name of the function changes ("a drunk is standing" means - will fall). So,
cos (π / 2 + α) = - sin α.
We stand at 2π. Since -α - we go back, that is, clockwise. We get to the IV quarter, where the tangent has a sign “-“. The name of the function does not change (the diameter is horizontal, "the drunk is already lying"). Thus, tg (2π-α) = - tgα.
3) ctg² (3π / 2-α) =?
Examples in which the function is raised to an even power are even easier to solve. The even degree "-" removes, that is, you just need to find out whether the name of the function changes or remains. The diameter is vertical (there is a fraction, "the drunk is standing", will fall), the name of the function changes. We get: ctg² (3π / 2-α) = tg²α.
There are two rules for using cast formulas.
1. If the angle can be represented as (π / 2 ± a) or (3 * π / 2 ± a), then function name changes sin to cos, cos to sin, tg to ctg, ctg to tg. If the angle can be represented as (π ± a) or (2 * π ± a), then the function name remains unchanged.
Look at the picture below, it shows schematically when to change the sign and when not.
2. The rule "what you were, so you stayed."
The sign of the reduced function remains the same. If the original function had a plus sign, then the reduced function also has a plus sign. If the original function had a minus sign, then the reduced function also has a minus sign.
The figure below shows the signs of the main trigonometric functions depending on the quarter.

Evaluate Sin (150˚)
Let's use the casting formulas:
Sin (150˚) is in the second quarter, according to the figure, we see that the sin sign in this quarter is +. This means that the reduced function will also have a plus sign. We applied the second rule.
Now 150˚ = 90˚ + 60˚. 90˚ is π / 2. That is, we are dealing with the case of π / 2 + 60, therefore, according to the first rule, we change the function from sin to cos. As a result, we get Sin (150˚) = cos (60˚) = ½.
If desired, all reduction formulas can be summarized in one table. But it's still easier to remember these two rules and use them.
Need help with your studies?

Previous topic:
Definition. Reduction formulas are called formulas that allow you to go from trigonometric functions of the form to functions of the argument. With their help, the sine, cosine, tangent and cotangent of an arbitrary angle can be reduced to the sine, cosine, tangent and cotangent of an angle from the interval from 0 to 90 degrees (from 0 to radians). Thus, the casting formulas allow us to switch to working with angles within 90 degrees, which is undoubtedly very convenient.
Casting formulas:

There are two rules for using cast formulas.
1. If the angle can be represented as (π / 2 ± a) or (3 * π / 2 ± a), then function name changes sin to cos, cos to sin, tg to ctg, ctg to tg. If the angle can be represented as (π ± a) or (2 * π ± a), then the function name remains unchanged.
Look at the picture below, it shows schematically when to change the sign, and when not

2. The sign of the reduced function remains the same. If the original function had a plus sign, then the reduced function also has a plus sign. If the original function had a minus sign, then the reduced function also has a minus sign.
The figure below shows the signs of the main trigonometric functions depending on the quarter.

Example:
Calculate
Let's use the casting formulas:
Sin (150˚) is in the second quarter, according to the picture we see that the sin sign in this quarter is "+". This means that the reduced function will also have a "+" sign. We applied the second rule.
Now 150˚ = 90˚ + 60˚. 90˚ is π / 2. That is, we are dealing with the case of π / 2 + 60, therefore, according to the first rule, we change the function from sin to cos. As a result, we get Sin (150˚) = cos (60˚) = ½.
And one more problem B11 on the same topic - from the real exam in mathematics.
A task. Find the meaning of the expression:
In this short video tutorial, we will learn how to apply reduction formulas for solving real problems B11 from the exam in mathematics. As you can see, we have before us two trigonometric expressions, each of which contains sines and cosines, as well as some pretty brutal numeric arguments.
Before solving these problems, let's remember what the casting formulas are. So, if we have expressions like:
Then we can get rid of the first term (of the form k · π / 2) according to special rules. Let's draw a trigonometric circle, mark the main points on it: 0, π / 2; π; 3π / 2 and 2π. Then we look at the first term under the sign of the trigonometric function. We have:
- If the term we are interested in lies on the vertical axis of the trigonometric circle (for example: 3π / 2; π / 2, etc.), then the original function is replaced by a co-function: the sine is replaced by the cosine, and the cosine, on the contrary, by the sine.
- If our term lies on the horizontal axis, then the original function does not change. We just remove the first term in the expression - and that's it.
Thus, we get a trigonometric function that does not contain terms of the form k · π / 2. However, the work with the reduction formulas does not end there. The fact is that in front of our new function, obtained after "discarding" the first term, there may be a plus or minus sign. How to identify this sign? Now we will find out.
Imagine that the angle α remaining inside the trigonometric function after the transformations has a very small degree measure. But what does "small measure" mean? Suppose α ∈ (0; 30 °) - this is quite enough. Consider, for example, a function:
![]()
Then, following our assumptions that α ∈ (0; 30 °), we conclude that the angle 3π / 2 - α lies in the third coordinate quarter, i.e. 3π / 2 - α ∈ (π; 3π / 2). We recall the sign of the original function, i.e. y = sin x on this interval. Obviously, the sine in the third coordinate quarter is negative, since by definition sine is the ordinate of the end of the moving radius (in short, sine is the y coordinate). Well, and the y-coordinate in the lower half-plane always takes negative values. Hence, in the third quarter, y is also negative.
Based on these reflections, we can write the final expression:
![]()
Problem B11 - Option 1
These same techniques are quite suitable for solving problem B11 from the exam in mathematics. The only difference is that in many real problems B11, instead of the radian measure (i.e. numbers π, π / 2, 2π, etc.), a degree measure is used (i.e. 90 °, 180 °, 270 ° and etc.). Let's take a look at the first task:
Let's deal with the numerator first. cos 41 ° is a non-tabular value, so we can't do anything with it. Let's leave it that way for now.
Now we look at the denominator:
sin 131 ° = sin (90 ° + 41 °) = cos 41 °
Obviously, we have a reduction formula, so sine was replaced by cosine. In addition, the 41 ° angle lies on the segment (0 °; 90 °), i.e. in the first coordinate quarter - exactly as required to apply the cast formulas. But then 90 ° + 41 ° is the second coordinate quarter. The original function y = sin x is positive there, so we put a plus sign in front of the cosine at the last step (in other words, we did not put anything).
The last element to be dealt with is:
cos 240 ° = cos (180 ° + 60 °) = −cos 60 ° = −0.5
Here we see that 180 ° is the horizontal axis. Consequently, the function itself will not change: there was a cosine - and the cosine will also remain. But again the question arises: will plus or minus stand in front of the resulting expression for cos 60 °? Note that 180 ° is the third coordinate quarter. The cosine is negative there, therefore, in front of the cosine, as a result, there will be a minus sign. In total, we get the construction −cos 60 ° = −0.5 - this is a tabular value, so everything is easy to calculate.
Now we substitute the resulting numbers into the original formula and get:
As you can see, the number cos 41 ° in the numerator and denominator of the fraction can be easily canceled, and the usual expression remains, which is equal to −10. In this case, the minus can either be taken out and placed before the sign of the fraction, or "kept" next to the second factor until the very last step of the calculations. The answer is -10 anyway. That's it, problem B11 is solved!
Problem B14 - Option 2
Let's move on to the second task. Before us is a fraction again:
Well, we have 27 ° in the first coordinate quarter, so we will not change anything here. But sin 117 ° must be painted (so far without any square):
sin 117 ° = sin (90 ° + 27 °) = cos 27 °
Obviously before us again reduction formula: 90 ° is the vertical axis, hence the sine will change to cosine. In addition, the angle α = 117 ° = 90 ° + 27 ° lies in the second coordinate quarter. The original function y = sin x is positive there, therefore, a plus sign remains in front of the cosine after all transformations. In other words, nothing is added there - so we leave it: cos 27 °.
We return to the original expression that needs to be calculated:
As you can see, after the transformations, the main trigonometric identity appeared in the denominator: sin 2 27 ° + cos 2 27 ° = 1. Total −4: 1 = −4 - so we found the answer to the second problem B11.
As you can see, with the help of reduction formulas, such problems from the exam in mathematics are solved literally in a couple of lines. No sines of the sum and cosines of the difference. All we need to remember is just the trigonometric circle.
 Who and how makes money on import substitution and innovations in agriculture R
Who and how makes money on import substitution and innovations in agriculture R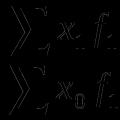 What is the industrial production index, its role and calculation
What is the industrial production index, its role and calculation Calculation of the design population of the city Term in metallurgy
Calculation of the design population of the city Term in metallurgy