Multiplication of fractions with different signs. Multiplication and division of negative numbers. Multiplication of numbers with different signs (6th grade)

Now let's figure it out with multiplication and division.

Suppose we need to multiply +3 to -4. How to do it?

Let's consider such a case. Three people climbed into debt, and every 4 dollar debt. What is the total debt? In order to find it, it is necessary to fold all three debt: 4 dollars + 4 dollars + 4 dollars \u003d 12 dollars. We decided that the addition of three numbers 4 is indicated as 3 × 4. Since in this case we are talking about the debt, before 4 there is a sign "-". We know that the total debt is equal to 12 dollars, so now our task has the form 3x (-4) \u003d - 12.

We will get the same result if, by the condition of the task, each of the four people has a debt of 3 dollars. In other words, (+4) x (-3) \u003d - 12. And since the order of the factors does not matter, we obtain (-4) x (+3) \u003d - 12 and (+4) x (-3) \u003d - 12.

Let's summarize the results. With multiplying one positive and one negative number, the result will always be a negative number. The numerical amount of the answer will be the same as in the case of positive numbers. Work (+4) x (+3) \u003d + 12. The presence of a sign "-" affects only a sign, but does not affect the numerical value.

And how to multiply two negative numbers?

Unfortunately, this topic is very difficult to come up with a suitable example from life. It is easy to imagine a debt in the amount of 3 or 4 dollars, but it is absolutely impossible to imagine -4 or -3 people who climbed into debt.

Perhaps we will go different ways. In multiplication, when a sign of one of the multipliers changes the sign of the work. If we change signs from both multipliers, we must change twice sign of workFirst, with a positive on a negative, and then on the contrary, with a negative on a positive, that is, the work will have an initial sign.

Consequently, it is quite logical, although it is slightly strange that (-3) x (-4) \u003d + 12.

Sign position When multiply changed in this way:

positive number x positive number \u003d positive number;
negative number x positive number \u003d negative number;
positive number x Negative number \u003d negative number;
negative number x negative number \u003d positive number.

In other words, multipliering two numbers with the same signs, we get a positive number. Multiplying two numbers with different signswe get a negative number.

The same rule is valid for the opposite multiplication - for.

You can easily make sure by spending inverse operations multiplication. If in each of the examples given above, you multiply the private per divider, then get divisible, and make sure it has the same sign, for example (-3) x (-4) \u003d (+ 12).

Because winter is soon, then it's time to think about what to rebuild your iron horse, whatever it is to slide on ice and feel confident in winter roads. You can, for example, take the bus of Yokohama on the site: mvo.ru or some others, most importantly, whatever, more information And you can find prices on the site Mvo.ru.

In this article we will deal with multiplying numbers with different signs. Here we first formulate a rule of multiplying a positive and negative number, justify it, and then consider the application of this rule when solving examples.

Navigating page.

Multiplication rule numbers with different signs

Multiplying a positive number on a negative, as well as a negative on a positive, is carried out at the following multiply multiplication rules with different signs: To multiply the numbers with different signs, you need to multiply, and to put a minus sign before the work received.

We write this rule In letterproof. For any positive actual number A and a valid negative number -B equality. a · (-b) \u003d - (| a | · | b |) , as well as for a negative number, and a positive number B rightly equality (-A) · b \u003d - (| a | · | b |) .

The rule of multiplication of numbers with different signs is fully consistent with properties of action with valid numbers. Indeed, on their basis it is easy to show that for real and positive numbers a and b is the chain of the equalities of the form a · (-b) + a · b \u003d a · ((- b) + b) \u003d a · 0 \u003d 0, which proves that A · (-b) and A · b are opposite numbers, whence the equality A · (-b) \u003d - (A · b). And from it follows the fairness of the multiplication rule.

It should be noted that the voiced rule of multiplication of numbers with different signs is fair both for real numbers and for rational numbers and for integers. This follows from the fact that actions with rational and integers possess the same properties that were used in the proof above.

It is clear that multiplication of numbers with different signs according to the obtained rule is reduced to multiplying positive numbers.

It remains only to consider the examples of applying a disassembled multiplication rule when multiplying numbers with different signs.

Examples of multiplication of numbers with different signs

We will analyze the solutions of several examples of multiplication of numbers with different signs. Let's start with a simple case to focus on the steps of the rule, and not on the computational difficulties.

Example.

Perform a multiplication of a negative number -4 to a positive number 5.

Decision.

According to the rule of multiplication of numbers with different signs, we first need to multiply the modules of the initial multipliers. Module -4 is 4, and the module 5 is 5, and the multiplication of natural numbers 4 and 5 gives 20. Finally, it remains to put a minus sign before the number it obtained, we have -20. The multiplication is completed.

A brief solution can be written as follows: (-4) · 5 \u003d - (4 · 5) \u003d - 20.

Answer:

(-4) · 5 \u003d -20.

When multiplying fractional numbers with different signs, you need to be able to perform multiplication of ordinary fractions, multiplying decimal fractions and combinations with natural and mixed numbers.

Example.

Spend multiplication of numbers with different signs 0, (2) and.

Decision.

After transferring the periodic decimal fraction in an ordinary fraction, as well as by performing a transition from a mixed number to incorrect fraction, from the original work We will come to the work ordinary fractions With different signs of the species. This product according to the rule of multiplication of numbers with different signs is equal. It remains only to multiply ordinary fractions in brackets, we have .

Navigating page.

Multiplication rule numbers with different signs

We write this rule in the alphabet. For any positive actual number A and a valid negative number -B equality. a · (-b) \u003d - (| a | · | b |) , as well as for a negative number, and a positive number B rightly equality (-A) · b \u003d - (| a | · | b |) .

It should be noted that the voiced rule of multiplication of numbers with different signs is fair both for valid numbers and for rational numbers And for integers. This follows from the fact that actions with rational and integers possess the same properties that were used in the proof above.

It is clear that multiplication of numbers with different signs according to the obtained rule is reduced to multiplying positive numbers.

It remains only to consider the examples of applying a disassembled multiplication rule when multiplying numbers with different signs.

Examples of multiplication of numbers with different signs

Perform a multiplication of a negative number -4 to a positive number 5.

According to the rule of multiplication of numbers with different signs, we first need to multiply the modules of the initial multipliers. Module -4 is 4, and the module 5 is 5, and multiplication natural numbers 4 and 5 gives 20. Finally, it remains to put a minus sign before the number it obtained, we have -20. The multiplication is completed.

A brief solution can be written as follows: (-4) · 5 \u003d - (4 · 5) \u003d - 20.

(-4) · 5 \u003d -20.

Spend multiplication of numbers with different signs 0, (2) and.

By transferring the transition of a periodic decimal fraction to an ordinary fraction, as well as by performing a transition from a mixed number to incorrect fraction, we will come to the product of ordinary fractions with different signs of the species. This product according to the rule of multiplication of numbers with different signs is equal. It remains only to multiply ordinary fractions in brackets, we have .

Separately, it is worth mentioning the multiplication of numbers with different signs when one or both factors are

Now let's figure it out with multiplication and division.

Suppose we need to multiply +3 to -4. How to do it?

And how to multiply two negative numbers?

Consequently, it is quite logical, although it is slightly strange that (-3) x (-4) \u003d + 12.

Sign position When multiply changed in this way:

positive number x positive number \u003d positive number;
negative number x positive number \u003d negative number;
positive number x Negative number \u003d negative number;
negative number x negative number \u003d positive number.

In other words, multipliering two numbers with the same signs, we get a positive number. Multiplying two numbers with different signs, we get a negative number.

The same rule is valid for the opposite multiplication - for.

Because winter is soon, then it's time to think about what to rebuild your iron horse, whatever it is to slide on ice and feel confident in winter roads. You can, for example, take the tires of Yokohama on the site: mvo.ru or some other, most importantly, whatever quality, more information and prices you can learn on the site Mvo.ru.

This article gives detailed review dividing numbers with different signs. At first, the number of dividing numbers with different signs is given. The examples of dividing positive numbers on negative and negative numbers are disassembled below.

Navigating page.

The division rule of numbers with different signs

In the article, the division of integers was obtained by the rule of division of integers with different signs. It can be extended to rational numbers, and for valid numbers, repeating all the arguments from this article.

So, the division rule of numbers with different signs It has the following wording: To split a positive number to a negative or negative number on a positive, it is necessary to divide into the divider module, and to put a minus sign before the obtained number.

We write this division rule with the help of letters. If the numbers A and B have different signs, then the formula is valid a: B \u003d - | A |: | B | .

Of the voiced rules, it is clear that the result of dividing numbers with different signs is a negative number. Indeed, since the divisory module and the divider module is positive, then their private has a positive number, and the minus sign makes it a negative number.

Note that the considered rule reduces the number of numbers with different signs to the division of positive numbers.

You can bring another formulation of the rules for dividing numbers with different signs: To divide the number A to the number B, you need to multiply by the number B -1, the reverse number B. I.e, a: B \u003d A · B -1 .

This rule can be used when it is possible to go beyond the set of integers (as far as not every integer has the opposite). In other words, it applies to the set of rational, as well as on a variety of valid numbers.

It is clear that this rule of dividing numbers with different signs allows you to go to multiplication from division.

The same rule is used in dividing negative numbers.

It remains to consider how this division rule of numbers with different signs is used when solving examples.

Examples of dividing numbers with different signs

Consider solutions of several characteristic examples of dividing numbers with different signsTo assimilate the principle of application of rules from the previous paragraph.

Divide the negative number -35 per positive number 7.

The division rule of numbers with different signs prescribes first to find the dividera and divider modules. The number -35 module is 35, and the number 7 module is 7. Now we need to divide the divisory module on the divider module, that is, it is necessary to divide 35 to 7. Remembering how the division of natural numbers is performed, we obtain 35: 7 \u003d 5. Remained last step The rules for dividing numbers with different signs - to put minus before the number obtained, we have -5.

That's all the solution :.

It was possible to proceed from another formulation of the rules for dividing numbers with different signs. In this case, you first find the number, the reverse divider 7. This number is an ordinary fraction of 1/7. In this way, . It remains to perform multiplication of numbers with different signs :. Obviously, we came to the same result.

(−35):7=−5 .

Calculate the private 8: (- 60).

According to the rules of dividing numbers with different signs we have 8:(−60)=−(|8|:|−60|)=−(8:60) . The resulting expression corresponds to a negative ordinary fraction (see the fission sign as a fractional line), you can reduce the fraction on 4, we get .

We write all the decision briefly :.

When dividing fractional rational numbers with different signs, their usually divide and divider are represented as ordinary fractions. This is due to the fact that with numbers in another record (for example, in decimal) is not always convenient to perform division.

The dividend module is equal, and the divider module is 0, (23). To divide the module divide on the divider module, we turn to ordinary fractions.

This lesson considers multiplication and division of rational numbers.

Design of lesson

Multiplying rational numbers

The rules for multiplying integers are valid for rational numbers. In other words, to multiply rational numbers, you need to be able to

Also, it is necessary to know the basic laws of multiplication, such as: Movement of multiplication, the combination law of multiplication, the distribution law of multiplication and multiplication by zero.

Example 1. Find an expression value

This is a multiplication of rational numbers with different signs. To multiply rational numbers with different signs, you need to multiply their modules and to put minus before the response received.

To see well to see what we are dealing with numbers who have different signs, enter each rational number in brackets together with your signs

The module of the number is equal, and the module of the number is equal. Moved the resulting modules as positive fractions, we got the answer, but before the answer was minus, as the rule required us. To ensure this minus before responding, the multiplication of the modules was performed in brackets, before which was minus.

A short solution is as follows:

Example 2. Find an expression value

Example 3. Find an expression value

This is a multiplication of negative rational numbers. To multiply negative rational numbers, you need to multiply their modules and in front of the response received to put plus

Solution for this example You can burn shorter:

Example 4. Find an expression value

The solution for this example can be written shorter:

Example 5. Find an expression value

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

A short solution will look much easier:

Example 6. Find an expression value

Transfer a mixed number to the wrong fraction. The rest will rewrite as it is

Received multiplication of rational numbers with different signs. Move the modules of these numbers and be minus before the response received. Recording with modules can be skipped to not clutter expression

The solution for this example can be written shorter

Example 7. Find an expression value

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

At first, the wrong shot turned out in the answer, but we allocated the whole part in it. note that whole part It was highlighted from the fraction module. The resulting mixed number was enclosed in brackets, before minus. This is done in order for the rule requirement. And the rule required that there was a minus before the response received.

The solution for this example can be written shorter:

Example 8. Find an expression value

First, change the number to the remaining number 5. Recording with modules will miss not to clutch expression.

Answer: The value of the expression equals -2.

Example 9. Find the value of the expression:

Translate mixed numbers In the wrong fraction:

Received multiplication of negative rational numbers. Move the modules of these numbers and in front of the response received, we will put a plus. Recording with modules can be skipped to not clutter expression

Example 10. Find an expression value

The expression consists of several factors. According to the combination law of multiplication, if the expression consists of several factors, then the work will not depend on the procedure. This allows us to calculate this expression in any order.

We will not be inventing the bike, and we calculate this expression from left to right in the order of the factory. Write with modules miss not to clutter expression

Third action:

Fourth action:

Answer: The value of the expression is equal

Example 11. Find an expression value

Remember the law of multiplication on zero. This law states that the work is zero, if at least one of the factors is zero.

In our example, one of the factors is zero, so without losing time responding that the value of the expression is zero:

Example 12. Find an expression value

The product is zero, if at least one of the factors is zero.

In our example, one of the factors is zero, so not losing time responding that the value of the expression Equally zero:

Example 13. Find an expression value

You can use the procedure for actions and first calculate the expression in brackets and multiply the result with a fraction.

You can still take advantage of the distribution law of multiplication - multiply every term of the fraction and the results obtained. In this way, we use.

According to the Procedure, if addition and multiplication is present in the expression, then first need to perform multiplication. Therefore, in the resulting new expression, we take in brackets those parameters that should be multiplied. So we will see well what actions perform earlier, and what later:

Third action:

Answer: The value of the expression equally

The solution for this example can be recorded significantly shorter. It will look like this:

It can be seen that this example could be solved even in the mind. Therefore, the expression analysis skill should be developed before it began. It is likely that it can be solved in the mind and save a lot of time and nerves. And in the control and exams, as it is known to be very expensive.

Example 14. Find an expression value -4.2 × 3.2

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

Pay attention to how the modules of rational numbers multiplied. In this case, in order to multiply the modules of rational numbers, it was required.

Example 15. Find an expression value -0.15 × 4

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

Pay attention to how the modules of rational numbers multiplied. In this case, in order to multiply the modules of rational numbers, it was necessary to be able.

Example 16. Find an expression value -4.2 × (-7.5)

This is a multiplication of negative rational numbers. Move the modules of these numbers and before the response received, we will put a plus

Division of rational numbers

The rules for dividing the integers are valid for rational numbers. In other words, to be able to share rational numbers, you need to be able to

The rest of the same methods of dividing ordinary and decimal fractions are used. To divide the ordinary fraction on another fraction, you need to multiply the first fraction to fraction, reverse second.

And to divide decimal fraction On another decimal fraction, you need to move the comma to the right to the right on so many numbers as they are after the comma in the divider, then make division as the usual number.

Example 1. Find the value of the expression:

This division of rational numbers with different signs. To calculate such an expression, you need to multiply the first fraction to the fraction, inverse second.

So, I will multiply the first fraction for the fraction inverse second.

Received multiplication of rational numbers with different signs. And how to calculate such expressions we already know. To do this, multiply the modules of these rational numbers and to put minus before the response received.

Take this example to the end. Recording with modules can be skipped to not clutter expression

Thus, the value of the expression is equal

A detailed solution is as follows:

A short solution will look like this:

Example 2. Find an expression value

This division of rational numbers with different signs. To calculate this expression, you need to multiply the first fraction to the fraction, inverse second.

The reverse for the second fraction is a fraction. For her and multiply the first fraction:

A short solution will look like this:

Example 3. Find an expression value

This division of negative rational numbers. To calculate this expression, again, you need to multiply the first fraction in the fraction inverse second.

The reverse for the second fraction is a fraction. For her and multiply the first fraction:

Received multiplication of negative rational numbers. As a calculated such expression, we already know. It is necessary to multiply the modules of rational numbers and before the response received is plus.

Dore this example to the end. Recording with modules can be skipped to not clutter expression:

Example 4. Find an expression value

To calculate this expression, you need the first number -3 to multiply by fraction, inverse fraction.

Reverse for a fraction this fraction. On her and multiply the first number -3

Example 6. Find an expression value

To calculate this expression, you need to multiply the first fraction by the number, reverse number 4.

The reverse for the number 4 is a fraction. On it and multiply the first fraction

Example 5. Find an expression value

To calculate this expression, you need to multiply the first fraction to the number, the reverse number -3

Inverse for a number -3 is a fraction. For her and multiply the first fraction:

Example 6. Find an expression -14,4: 1.8

This division of rational numbers with different signs. To calculate this expression, you need to divide the divide module to the divisor module and put a minus before the response received

Note how the divisory module was divided into the divider module. In this case, to make it right, it took to be able to be able.

If there is no desire to mess with decimal fractions (and it happens often), then these, then translate these mixed numbers into the wrong fraction, and then do the division directly.

We calculate the previous expression -14.4: 1.8 in this way. Transfer decimal fractions into mixed numbers:

Now we will transfer the resulting mixed numbers to the wrong fraction:

Now you can go directly to the division, namely split the fraction for the fraction. To do this, you need to multiply the first fraction, inverse the second:

Example 7. Find an expression value

We translate the decimal fraction -2.06 to the wrong fraction, and multiply this fraction for the fraction, inverse second:

Multi-storey fractions

Often you can find an expression in which the division of fractions is written using a fractional feature. For example, the expression can be recorded as follows:

What is the difference between expressions and? In fact, no difference. These two expressions carry the same meaning and between them can be put a sign of equality:

In the first case, the division sign is a colon and the expression is recorded in one line. In the second case, the division of fractions is written using a fractional feature. As a result, it turns out a fraction, which the people agreed to call multi-storey.

When meeting with such multi-storey expressions, you need to apply the same rules for dividing ordinary fractions. The first fraction must be multiplied by the fraction, inverse second.

Use in solving such fractions is extremely inconvenient, so you can write them in understandable, using a non-fractional line as a sign, and a colon.

For example, we write a multi-storey fraction in understandable. To do this, you first need to figure out where the first fraction and where the second, because it is not always possible to do it correctly. In multi-storey fractions there are several fractional traits that can be confused. The main fractional feature, which separates the first fraction from the second, is usually longer than the rest.

After determining the main fractional line, you can easily understand where the first fraction and where the second:

Example 2.

We find the main fractional line (it is the longest) and we see that the division of an integer -3 one is carried out on an ordinary fraction

And if we mistakenly accepted the second fractional feature for the main thing (the one is shorter), it would have been that we divide the fraction for an integer 5 in this case, even if this expression is to calculate correctly, the task will be solved incorrect because divisible in this The case is the number -3, and the divider - the fraction.

Example 3. We write in understandable form a multi-storey fraction

We find the main fractional line (it is the longest) and see that the fraction is carried out by an integer 2

And if we mistakenly accepted the first fractional feature for the main thing (the one is shorter), it would have done that we would divide the whole number -5 on the fraction in this case, even if this expression is true, the task will be solved incorrectly because divisible In this case, the fraction is, and the divider is an integer 2.

Despite the fact that multi-storey fractions are uncomfortable in work, we will face with them very often, especially when studying the highest mathematics.

Naturally, the translation of a multi-storey fraction in a clear species takes extra time and place. Therefore, you can use more fast method. This method is convenient and at the output allows you to get a ready-made expression in which the first fraction is already multiplied by fraction, inverse second.

This method is implemented as follows:

If the fraction is a four-storey, for example, like, the figure on the first floor is raised to the top floor. And the figure located on the second floor is raised by the third floor. The figures obtained need to connect the multiplication icons (×)

As a result, bypassing the intermediate record, we obtain a new expression in which the first fraction is already multiplied by the fraction, inverse second. Convenience and only!

To prevent errors when using this method, It can be guided by the following rule:

From the first to the fourth. From the second on the third.

In Rule we are talking about the floors. The number from the first floor should be raised on the fourth floor. And the number from the second floor you need to raise on the third floor.

Let's try to calculate the multi-storey fraction using the above rule.

So, the figure located on the first floor raise the fourth floor, and I raise the figure on the second floor to the third floor

As a result, bypassing the intermediate entry, we obtain a new expression in which the first fraction is already multiplied by the fraction, inverse second. Next, you can take advantage of the knowledge:

Let's try to calculate the multi-storey fraction using the new scheme.

There is only the first, second and fourth floors. The third floor is absent. But we do not move away from the main scheme: I raise the figure from the first floor to the fourth floor. And since there is no third floor, then leave the figure on the second floor, as is

As a result, bypassing the intermediate entry, we received a new expression, in which the first number -3 is already multiplied by the fraction, inverse second. Next, you can take advantage of the knowledge:

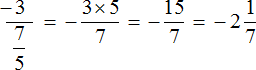
Let's try to calculate the multi-storey fraction using a new scheme.

There is only the second, third and fourth floors. The first floor is absent. Since there is no first floor, it is there for a fourth floor, but we can raise the number from the second floor to the third:

As a result, bypassing the intermediate entry, we received a new expression, in which the first fraction is already multiplied by the reverse divider. Next, you can take advantage of the knowledge:

Using variables

If the expression is complex and it seems to you that it will confuse you in the process of solving the problem, then part of the expression can be added to the variable and then work with this variable.

Mathematics often do. The challenging task is divided into more easy subtasks and solve them. Then they collect solved subtasks into one single integer. This is a creative process and it is studying for years, training hard.

The use of variables is justified when working with multi-storey fractions. For example:

Find an expression value

So, there is a fractional expression in the numerator and in the denominator fractional expressions. In other words, we are again a multi-storey fraction that we do not like that.

The expression located in the numerator can be entered into a variable with any name, for example:

But in mathematics in this case, the variables take the name from large Latin letters. Let's not violate this tradition, and we denote the first expression through the Latin Latin letter A

And the expression located in the denominator can be denoted through a large Latin letter B

Now our initial expression takes appearance. That is, we made a replacement numerical expression On the letter, pre-enlightened the numerator and denominator in Variables A and B.

Now we can separately calculate the values \u200b\u200bof the variable A and the value of the variable B. The finished values \u200b\u200bwe insert into the expression.

Find the value of the variable A.

Find the value of the variable B.

Now we substitute in the main expression instead of variables a and b of their meanings:

We got a multi-storey fraction in which you can use the scheme "from the first to the fourth, from the second to the third", that is, the figure located on the first floor to raise on the fourth floor, and the figure is on the second floor to raise the third floor. Further computation will not be much difficulty:

Thus, the value of the expression is -1.

Of course, we considered the simplest exampleBut our goal was to know how to use variables to facilitate yourself tasks to minimize error assumptions.

We also note that the solution for this example can be recorded without applying variables. It will look like

This solution is faster and short and in this case it is more expedient to write it down, but if the expression is complex, consisting of several parameters, brackets, roots and degrees, it is advisable to calculate it in several steps, enters part of its expressions into variables.

Did you like the lesson?
Join our new group VKontakte and start receiving notifications about new lessons

Objectives lesson:

Educational:

formulation of multiplication rules of numbers with the same and different signs;
mastering and improving multiplication skills with different signs.

Developing:

development of mental operations: comparison, generalization, analysis, analogy;
development of skills independent work;
expansion of the horizons of students.

Educational:

raising the culture of registration of records;
raising responsibility, attention;
education of interest in the subject.

Type of lesson: Studying a new material.

Equipment: Computer, multimediaRector, cards for the game "Mathematical battle", tests, knowledge accounting cards.

On the walls posters:

Knowledge is the most excellent of possessions. Everyone strive for him, it does not come.
Al-Biruni.
In all, I want to reach the very essence ...
B. Pasternak

Lesson plan

Organizational moment (1 min).
introduction Teachers (3 min).
Oral work (10 min).
Presentation of material (15 min).
Mathematical chain (5 min).
Homework (2 minutes).
Test (6 min).
Outcome lesson (3 min).

During the classes

I. Organizational moment

readiness of students to the lesson.

II. Teacher's introductory word

Guys, we met today not in vain, but for fruitful work: getting knowledge.

Since there is a universe,
There is no such, who would not need know.
What we do not take the language and age,
Always sought to know a person ...
Rudaki

In the lesson we will study new Material, fasten it, work yourself, evaluate yourself and your comrades. Everyone on the table is a card accounting card in which our lesson is divided into stages. You earned points on different stages The lesson you yourself will be submitted to this card. And at the end of the lesson we will summarize the results. Put these cards for a prominent place.

III. Oral work (in the form of the game "Mathematical Fight")

Guys before proceeding to new topic, Repeat the previously learned. Everyone in the desk lies a sheet with a "mathematical battle" game. In the vertical and horizontal columns are recorded the numbers that need to be folded. These numbers are marked by points. Answers write to those cells on the field where there are points.

Three minutes for execution. Started work.

And now they exchanged work with a subsidement on the desk and check them from each other. If you think that the answer is wrong, then neatly cross it up and enter the correct one. Check.

And now you will verify the answers with the screen ( the correct answers are designed on the screen).

For properly solved

5 tasks set 5 points;
4 tasks - 4 points;
3 tasks - 3 points;
2 tasks - 2 points;
1 task - 1 point.

Well done. Postponed everything aside. Guys, in their card accounting cards will bring the number of points scored for "mathematical battle" ( Attachment 1).

IV. Presentation of material

Open workbooks. We write down the number, cool job.

What actions on positive and negative numbers do you know?
How to fold two negative numbers?
How to fold two numbers with different signs?
How to subtract numbers with different signs?
You always use the word "module". And what is called the module number but?

The current topic of the lesson is also associated with the action over the numbers of different signs. But she hid in an anagram, in which it is necessary to swap letters and get a familiar word. Let's try to solve.

Enegsenny

Write the subject of the lesson: "Multiplication".

The purpose of our lesson: to get acquainted with multiplication of positive and negative numbers and formulate the multiplication rules of the numbers both with the same and different signs.

All attention to the board. Before you, a table with tasks, deciding which we will formulate the rules for multiplying positive and negative numbers.

2 * 3 \u003d 6 ° C;
-2 * 3 \u003d -6 ° C;
-2 * (- 3) \u003d 6 ° C;
2 * (- 3) \u003d -6 ° C;

1. The air temperature rises every hour by 2 ° C. Now the thermometer shows 0 ° C ( Appendix 2. - Sigdition) (Slide 1 on the computer).

How much did you get?(6 ° FROM).
Someone will write down the decision on the board, and we are all in notebooks.
Let's look at the thermometer, faithful we got the answer? (Slide 2 on the computer).

2. The air temperature drops every hour by 2 ° C. Now the thermometer shows 0 ° C (Slide 3 on the computer). What air temperature will show the thermometer after 3 hours?

How much did you get?(–6 ° FROM).
We write the appropriate solution on the board and in notebooks. Analogy with task 1.
. (Slide 4 on the computer).

3. The air temperature decreases every hour by 2 ° C. Now the thermometer shows 0 ° C (Slide 5 on the computer).

How much did you get?(6 ° FROM).
We write the appropriate solution on the board and in notebooks. Analogy with tasks 1 and 2.
Compare the result with the thermometer reading. (slide 6 on the computer).

4. The air temperature rises every hour by 2 ° C. Now the thermometer shows 0 ° C (Slide 7 on the computer). What air temperature showed a thermometer 3 hours ago?

How much did you get?(–6 ° FROM).
We write the appropriate solution on the board and in notebooks. Analogy with tasks 1-3.
Compare the result with the thermometer reading. (Slide 8 on the computer).

Look at your results. When multiplying numbers with the same signs (examples 1 and 3), what sign received the answer? (positive).

Okay. But in example 3, both multipliers are negative, and the answer was positive. What mathematical concept makes it from negative numbers to move to positive? (module).

Attention Rule: To multiply two numbers with the same signs, you must multiply their modules and put the "Plus" sign before the result. (2 people repeat).

Let's come back for example 3. What are the modules (-2) and (-3)? Move these modules. How much did you get? What sign?

When multiplying numbers with different signs (examples 2 and 4), what sign did the answer get? (negative).

Word the multiplication rule itself with different signs.

Rule: When multiplying numbers with different signs, you need to multiply their modules and put the "minus" sign before the result. (2 people repeat).

Let us return to Examples No. 2 and No. 4. What are the modules of their multipliers? Move these modules. How much did you get? What sign must be put as a result?

With the help of these two rules, you can multiply the fractions: decimal, mixed, ordinary.

Before you, on the board, several examples. Three decide with me, and the rest on their own. Pay attention to the record and design.

Well done. We will open textbooks and note the rules that need to be learned to the next lesson (Page 190, §7 (paragraph 35)). Knowing these rules will help further quickly master the division of positive and negative numbers.

V. Mathematical chain

And now Dunno wants to check how you learned the new material, and ask you a few questions. Decision and answers are definitely recorded in notebooks ( Appendix 3. - Mathematical chain).

Computer presentation
Hello guys. I see you are very clever and inquisitive, so I want to ask you a few questions. Be careful, especially with signs.
My first question: multiply (-3) on (-13).
The second question: multiply what they got in the first task on (–0,1).
The third question: the result of the second task is to multiply on (-2).
Fourth question: multiply (-1/3) on the result of the third task.
And the last, fifth question: Calculate the temperature of mercury freezing, multiplies the result of the fourth task by 15.
Thanks for the job. I wish you success.

Guys, let's check how we coped with the tasks. Stand all.

How much did they get in the first task?

Who has another answer, sat down, and who sat down, in the knowledge card card, we put themselves for the mathematical chain of 0 points. The rest do not put anything.

How much did they get in the second task?

Who has a different answer, sat down, and put themselves in the card accounting card for the mathematical chain 1 point.

How much did they get in the third task?

Who has a different answer, and set themselves in the card accounting card for the mathematical chain of 2 points.

How much did they get in the fourth task?

Who has a different answer, sat down, and put yourself in the card accounting card for the mathematical chain of 3 points.

How much did they get in the fifth job?

Who has a different answer, sat down, and put themselves in the card accounting card for the mathematical chain of 4 points. The remaining guys decided right all 5 tasks. Sit down, you put yourself in a card accounting card 5 points for a mathematical chain.

What is the temperature of mercury freezing?(–39 ° С).

Vi. Homework

§7 (paragraph 35, page 190), №1121- Tutorial: Mathematics. Grade 6: [N.Ya.Vilenkin et al.]

Creative task: Make a task to multiply positive and negative numbers.

VII. Test

Go to the next lesson stage: test performing ( Appendix 4.).

You need to solve tasks and circle a number of correct response. For the first two crowded tasks, you will receive 1 point, for 3 tasks - 2 points, for 4 tasks - 3 points. Started work.

Δ -1 score;
O -2 score;
-3 points.

And now the numbers of the correct answers will write to the table under the test. Check the results obtained. You in your empty cells should turn out the number 1418 (I write down on the board). Who got it - puts in the card account of 7 points. Who made mistakes, then the number of points scored only for the crowded tasks put in the knowledge card.

It was 1418 days the great lasted Patriotic War, the victory in which the Russian people went to the hard price. And on May 9, 2010, we will celebrate the 65th anniversary of the victory over the fascist Germany.

VIII. Total lesson

Now we will calculate the total number of points you scored for a lesson, and the results will be in the card accounting card. After renting these cards.

15 - 17 points - rating "5";
10 - 14 points - rating "4";
Less than 10 points - rating "3".

Raise your hands who got "5", "4", "3".

What topic did we consider today?
How to multiply the numbers with the same signs; With different signs?

So, our lesson approached the end. I want to tell you thanks for the work in the lesson.