Paano makalkula ang inverse matrix. Maghanap ng inverse matrix online. Gamit ang calculator

Matrix Algebra - Inverse Matrix

baligtad na matris

baligtad na matris Ang isang matrix ay tinatawag na, kapag pinarami pareho sa kanan at sa kaliwa ng isang ibinigay na matrix, ay nagbibigay ng identity matrix.
Ipahiwatig ang kabaligtaran ng matrix sa matrix PERO sa pamamagitan ng , pagkatapos ay ayon sa kahulugan na nakukuha natin:

saan E ay ang identity matrix.
parisukat na matris tinawag hindi espesyal (hindi nabubulok) kung ang determinant nito ay hindi katumbas ng zero. Kung hindi, ito ay tinatawag espesyal (mabulok) o isahan.

Mayroong isang teorama: bawat non-singular matrix ay may inverse matrix.

Ang operasyon ng paghahanap ng inverse matrix ay tinatawag apela matrice. Isaalang-alang ang matrix inversion algorithm. Hayaang magbigay ng non-singular matrix n-ika-utos:

kung saan Δ = det A ≠ 0.

Algebraic na elementong pandagdag matrice n-ika-utos PERO ang determinant ng matrix ( n–1)-ika-order na nakuha sa pamamagitan ng pagtanggal i-ika linya at j-th column ng matrix PERO:

Gumawa tayo ng tinatawag na kalakip matris:

nasaan ang algebraic complements ng mga kaukulang elemento ng matrix PERO.
Tandaan na ang mga algebraic na pandagdag sa mga elemento ng row ng matrix PERO ay inilalagay sa kaukulang mga column ng matrix Ã , iyon ay, ang matrix ay inilipat nang sabay-sabay.
Paghahati sa lahat ng elemento ng matrix Ã on Δ - ang halaga ng determinant ng matrix PERO, nakukuha namin ang inverse matrix bilang isang resulta:

Napansin namin ang isang bilang ng mga espesyal na katangian ng inverse matrix:
1) para sa isang ibinigay na matrix PERO inverse matrix nito ay ang isa lamang;
2) kung mayroong isang kabaligtaran na matrix , kung gayon kanang baligtad at kaliwa pabalik ang mga matrice ay nag-tutugma dito;
3) ang isang espesyal na (degenerate) square matrix ay walang inverse matrix.

Ang mga pangunahing katangian ng inverse matrix:
1) ang determinant ng inverse matrix at ang determinant ng orihinal na matrix ay reciprocals;
2) ang inverse matrix ng produkto ng square matrices ay katumbas ng produkto ng inverse matrices ng mga kadahilanan, na kinuha sa reverse order:

3) ang transposed inverse matrix ay katumbas ng inverse matrix mula sa ibinigay na transposed matrix:

HALIMBAWA Kalkulahin ang kabaligtaran ng matrix ng ibinigay na isa.

baligtad na matris ay isang matris A -1, kapag pinarami kung saan ang ibinigay na paunang matrix A nagbibigay ng identity matrix E:

AA −1 = A −1 A =E.

Inverse matrix na pamamaraan.

Inverse matrix na pamamaraan- ito ay isa sa mga pinakakaraniwang pamamaraan para sa paglutas ng mga matrice at ginagamit upang mga solusyon ng mga sistema ng linear algebraic equation(SLAE) sa mga kaso kung saan ang bilang ng mga hindi alam ay tumutugma sa bilang ng mga equation.

Magkaroon ng sistema n linear equation na may n hindi alam:

Ang ganitong sistema ay maaaring isulat bilang isang matrix equation A*X=B,

saan
- system matrix,

- hanay ng mga hindi alam,

- hanay ng mga libreng coefficient.

Mula sa nagmula na matrix equation, ipinapahayag namin ang X sa pamamagitan ng pagpaparami ng magkabilang panig ng matrix equation sa kaliwa ng A-1, na nagreresulta sa:

A -1 * A * X = A -1 * B

Alam na A-1*A=E, pagkatapos E*X=A-1*B o X=A-1*B.

Ang susunod na hakbang ay upang matukoy ang inverse matrix A-1 at pinarami sa hanay ng mga libreng miyembro B.

Inverse Matrix sa Matrix A umiiral lamang kapag det A≠ 0 . Dahil dito, kapag nilulutas ang SLAE sa pamamagitan ng inverse matrix method, ang unang hakbang ay ang paghahanap det A. Kung ang det A≠ 0 , kung gayon ang sistema ay may isang solusyon lamang, na maaaring makuha sa pamamagitan ng inverse matrix na paraan, kung det A = 0, pagkatapos ay ganoong sistema paraan ng inverse matrix ay hindi naresolba.

Inverse matrix solution.

Pagkakasunod-sunod ng mga aksyon para sa kabaligtaran na mga solusyon sa matrix:

Kunin ang matrix determinant A. Kung ang determinant ay mas malaki kaysa sa zero, mas malulutas namin ang inverse matrix, kung ito ay katumbas ng zero, kung gayon ang inverse matrix ay hindi matatagpuan dito.
Paghahanap ng transposed matrix AT.
Naghahanap kami ng mga algebraic complement, pagkatapos nito ay pinapalitan namin ang lahat ng elemento ng matrix ng kanilang mga algebraic complement.
Kinokolekta namin ang inverse matrix mula sa mga algebraic na karagdagan: hinahati namin ang lahat ng mga elemento ng resultang matrix sa pamamagitan ng determinant ng unang ibinigay na matrix. Ang huling matrix ay ang nais na kabaligtaran na matrix na may paggalang sa orihinal.

Ang algorithm sa ibaba kabaligtaran na mga solusyon sa matrix mahalagang pareho sa itaas, ang pagkakaiba ay nasa ilang hakbang lamang: una sa lahat, tinutukoy namin ang mga algebraic na pagdaragdag, at pagkatapos ay kinakalkula namin ang matrix ng unyon C.

Alamin kung ang ibinigay na matrix ay parisukat. Sa kaso ng isang negatibong sagot, nagiging malinaw na hindi maaaring magkaroon ng isang kabaligtaran na matrix para dito.
Alamin kung ang ibinigay na matrix ay parisukat. Sa kaso ng isang negatibong sagot, nagiging malinaw na hindi maaaring magkaroon ng isang kabaligtaran na matrix para dito.
Kinakalkula namin ang mga algebraic na pagdaragdag.
Binubuo namin ang allied (mutual, attached) matrix C.
Bumubuo kami ng kabaligtaran na matrix mula sa mga algebraic na pagdaragdag: lahat ng elemento ng magkadugtong na matrix C hatiin sa determinant ng inisyal na matrix. Ang resultang matrix ay ang nais na kabaligtaran na matrix na may paggalang sa ibinigay.
Sinusuri namin ang gawaing nagawa: pinarami namin ang inisyal at nagreresultang mga matrice, ang resulta ay dapat na ang identity matrix.

Ito ay pinakamahusay na gawin sa isang nakalakip na matrix.

Theorem: Kung magtatalaga tayo ng identity matrix ng parehong pagkakasunud-sunod sa isang square matrix sa kanang bahagi at gagawing unit matrix ang initial matrix sa kaliwa gamit ang elementary transformations sa mga row, kung gayon ang nakuha sa kanang bahagi ay magiging baligtad sa ang una.

Isang halimbawa ng paghahanap ng inverse matrix.

Mag-ehersisyo. Para sa matrix hanapin ang kabaligtaran sa pamamagitan ng magkadugtong na pamamaraan ng matrix.

Desisyon. Nagdaragdag kami sa ibinigay na matrix PERO sa kanan, ang identity matrix ng 2nd order:

Ibawas ang ika-2 mula sa unang linya:

Ibawas ang unang 2 mula sa pangalawang linya:

Ang matrix na $A^(-1)$ ay tinatawag na inverse ng square matrix $A$ kung $A^(-1)\cdot A=A\cdot A^(-1)=E$, kung saan $E $ ay ang identity matrix, ang pagkakasunod-sunod nito ay katumbas ng pagkakasunod-sunod ng matrix na $A$.

Ang non-singular matrix ay isang matrix na ang determinant ay hindi katumbas ng zero. Alinsunod dito, ang isang degenerate matrix ay isa na ang determinant ay katumbas ng zero.

Ang inverse matrix na $A^(-1)$ ay umiiral kung at tanging kung ang matrix na $A$ ay nonsingular. Kung ang inverse matrix na $A^(-1)$ ay umiiral, ito ay natatangi.

Mayroong ilang mga paraan upang mahanap ang kabaligtaran ng isang matrix, at titingnan natin ang dalawa sa kanila. Tatalakayin ng pahinang ito ang magkadugtong na pamamaraan ng matrix, na itinuturing na pamantayan sa karamihan ng mas matataas na kurso sa matematika. Ang pangalawang paraan upang mahanap ang inverse matrix (paraan ng elementarya na pagbabago), na kinabibilangan ng paggamit ng Gauss method o ang Gauss-Jordan method, ay isinasaalang-alang sa ikalawang bahagi.

Adjoint (union) matrix method

Hayaang ibigay ang matrix na $A_(n\times n)$. Upang mahanap ang inverse matrix na $A^(-1)$, tatlong hakbang ang kailangan:

Hanapin ang determinant ng matrix na $A$ at siguraduhin na ang $\Delta A\neq 0$, i.e. na ang matrix A ay hindi nabubulok.
Bumuo ng algebraic complements $A_(ij)$ ng bawat elemento ng matrix $A$ at isulat ang matrix $A_(n\times n)^(*)=\left(A_(ij) \right)$ mula sa nahanap algebraic complements.
Isulat ang inverse matrix na isinasaalang-alang ang formula na $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Ang matrix na $(A^(*))^T$ ay madalas na tinutukoy bilang ang magkadugtong (mutual, allied) na matrix ng $A$.

Kung ang desisyon ay ginawa nang manu-mano, kung gayon ang unang pamamaraan ay mabuti lamang para sa mga matrice na medyo maliit na mga order: pangalawa (), pangatlo (), pang-apat (). Upang mahanap ang inverse matrix para sa mas mataas na order matrix, ginagamit ang iba pang mga pamamaraan. Halimbawa, ang pamamaraang Gauss, na tinalakay sa ikalawang bahagi.

Halimbawa #1

Hanapin ang matrix inverse sa matrix $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Dahil ang lahat ng elemento ng ikaapat na column ay katumbas ng zero, kung gayon ang $\Delta A=0$ (ibig sabihin, ang matrix na $A$ ay degenerate). Dahil $\Delta A=0$, walang matrix inverse sa $A$.

Sagot: matrix $A^(-1)$ ay wala.

Halimbawa #2

Hanapin ang inverse ng matrix sa matrix $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Magpatakbo ng tseke.

Ginagamit namin ang magkadugtong na pamamaraan ng matrix. Una, hanapin natin ang determinant ng ibinigay na matrix $A$:

$$ \Delta A=\kaliwa| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Dahil $\Delta A \neq 0$, kung gayon ang inverse matrix ay umiiral, kaya ipinagpatuloy namin ang solusyon. Paghahanap ng Algebraic Complements

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(aligned)

Bumuo ng isang matrix ng algebraic complements: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Ilipat ang resultang matrix: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (ang nagreresulta Ang matrix ay madalas na tinatawag na adjoint o unyon matrix sa matrix $A$). Gamit ang formula na $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, mayroon kaming:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\kanan) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

Kaya ang inverse matrix ay natagpuan: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \kanan) $. Upang suriin ang katotohanan ng resulta, sapat na suriin ang katotohanan ng isa sa mga pagkakapantay-pantay: $A^(-1)\cdot A=E$ o $A\cdot A^(-1)=E$. Suriin natin ang pagkakapantay-pantay na $A^(-1)\cdot A=E$. Upang hindi gaanong gumana sa mga fraction, papalitan namin ang matrix na $A^(-1)$ wala sa anyong $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\kanan)$ ngunit bilang $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \ end(array )\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( array)\kanan)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array )\kanan) =E $$

Sagot: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Halimbawa #3

Hanapin ang inverse ng matrix $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$. Magpatakbo ng tseke.

Magsimula tayo sa pagkalkula ng determinant ng matrix na $A$. Kaya, ang determinant ng matrix na $A$ ay:

$$ \Delta A=\kaliwa| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

Dahil ang $\Delta A\neq 0$, kung gayon ang inverse matrix ay umiiral, kaya't ipinagpatuloy namin ang solusyon. Nahanap namin ang mga algebraic na pandagdag ng bawat elemento ng ibinigay na matrix:

Bumubuo kami ng isang matrix ng mga algebraic na karagdagan at inilipat ito:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

Gamit ang formula na $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, nakukuha namin ang:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 at -3/26 at 37/26 \end(array) \right) $$

Kaya $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. Upang suriin ang katotohanan ng resulta, sapat na suriin ang katotohanan ng isa sa mga pagkakapantay-pantay: $A^(-1)\cdot A=E$ o $A\cdot A^(-1)=E$. Suriin natin ang pagkakapantay-pantay $A\cdot A^(-1)=E$. Upang hindi gaanong gumana sa mga fraction, papalitan namin ang matrix na $A^(-1)$ hindi sa anyong $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, ngunit bilang $\frac(1)(26)\ cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(array) \right) =\frac(1)(26)\cdot\left(\begin(array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (array) \right) =\left(\begin(array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

Ang tseke ay matagumpay na naipasa, ang inverse matrix na $A^(-1)$ ay natagpuan nang tama.

Sagot: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Halimbawa #4

Hanapin ang matrix inverse ng $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

Para sa isang matrix ng ikaapat na pagkakasunud-sunod, ang paghahanap ng inverse matrix gamit ang mga algebraic na pagdaragdag ay medyo mahirap. Gayunpaman, ang mga ganitong halimbawa ay matatagpuan sa mga gawaing kontrol.

Upang mahanap ang inverse matrix, kailangan mo munang kalkulahin ang determinant ng matrix $A$. Ang pinakamahusay na paraan upang gawin ito sa sitwasyong ito ay upang palawakin ang determinant sa isang hilera (column). Pinipili namin ang anumang row o column at hinahanap ang algebraic complement ng bawat elemento ng napiling row o column.

Halimbawa, para sa unang hilera nakukuha namin:

$$ A_(11)=\kaliwa|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\kanan|=556; \; A_(12)=-\left|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\kaliwa|\begin(array)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\kanan|= -536;\; A_(14)=-\left|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

Ang determinant ng matrix $A$ ay kinakalkula ng sumusunod na formula:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14 )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(nakahanay) $$

Algebraic complement matrix: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(array)\kanan)$.

Naka-attach na matrix: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\kanan)$.

Inverse matrix:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Ang pagsuri, kung ninanais, ay maaaring gawin sa parehong paraan tulad ng sa mga nakaraang halimbawa.

Sagot: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(array) \right) $.

Sa ikalawang bahagi, isa pang paraan ng paghahanap ng inverse matrix ang isasaalang-alang, na kinabibilangan ng paggamit ng mga pagbabagong-anyo ng Gauss method o ang Gauss-Jordan method.

ALGEBRAIC ADDITIONS AT MINORS

Magkaroon tayo ng third-order determinant: .

menor de edad naaayon sa elementong ito aij Ang pangatlong-order na determinant ay tinatawag na pangalawang-order na determinant na nakuha mula sa ibinigay na isa sa pamamagitan ng pagtanggal ng row at column sa intersection kung saan nakatayo ang ibinigay na elemento, i.e. i-ika linya at j-ika-kolum. Mga menor de edad na naaayon sa isang ibinigay na elemento aij kami ay magsasaad M ij.

Halimbawa, menor de edad M12 naaayon sa elemento isang 12, magkakaroon ng determinant 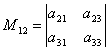, na nakukuha sa pamamagitan ng pagtanggal ng 1st row at 2nd column mula sa ibinigay na determinant.

Kaya, ang formula na tumutukoy sa third-order determinant ay nagpapakita na ang determinant na ito ay katumbas ng kabuuan ng mga produkto ng mga elemento ng 1st row at ang kanilang mga katumbas na menor de edad; habang ang menor ay naaayon sa elemento isang 12, ay kinukuha gamit ang “–” sign, i.e. maaaring isulat na

(1)

Katulad nito, maaaring ipakilala ng isa ang mga kahulugan ng mga menor de edad para sa mga determinant ng pangalawang order at mas mataas na mga order.

Ipakilala natin ang isa pang konsepto.

Algebraic na karagdagan elemento aij determinant ay tinatawag na menor nito M ij pinarami ng (–1) i+j .

Pagdaragdag ng elemento ng algebraic aij ipinapahiwatig Isang ij.

Mula sa kahulugan, nakukuha natin na ang koneksyon sa pagitan ng algebraic complement ng isang elemento at ang menor nito ay ipinahayag ng pagkakapantay-pantay. Isang ij= (–1) i+j M ij .

Halimbawa,

Halimbawa. Binigyan ng determinant. Hanapin A 13 , A 21 , A 32.

Madaling makita na gamit ang algebraic na mga pagdaragdag ng mga elemento, ang formula (1) ay maaaring isulat bilang:

Katulad ng formula na ito, maaaring makuha ng isa ang decomposition ng determinant sa mga elemento ng anumang row o column.

Halimbawa, ang agnas ng determinant sa mga elemento ng 2nd row ay maaaring makuha tulad ng sumusunod. Ayon sa property 2 ng determinant, mayroon tayong:

Palawakin natin ang nakuha na determinant ng mga elemento ng 1st row.

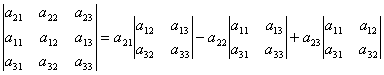(2)

Mula rito kasi ang pangalawang-order na mga determinant sa formula (2) ay ang mga menor de edad ng mga elemento isang 21, isang 22, isang 23. Kaya, , i.e. nakuha namin ang pagpapalawak ng determinant ng mga elemento ng 2nd row.

Katulad nito, maaaring makuha ng isa ang agnas ng determinant sa mga elemento ng ikatlong hilera. Gamit ang property 1 ng mga determinant (sa transposisyon), maaaring ipakita ng isa na ang mga katulad na pagpapalawak ay may bisa din para sa mga pagpapalawak sa mga elemento ng column.

Kaya, ang sumusunod na teorama ay totoo.

Theorem (sa pagpapalawak ng determinant sa isang naibigay na row o column). Ang determinant ay katumbas ng kabuuan ng mga produkto ng mga elemento ng alinman sa mga row (o column) nito at ang kanilang mga algebraic complement.

Ang lahat ng nasa itaas ay totoo para sa mga determinant ng anumang mas mataas na pagkakasunud-sunod.

Mga halimbawa.

INVERSE MATRIX

Ang konsepto ng isang inverse matrix ay ipinakilala lamang para sa square matrice.

Kung ang A ay isang square matrix, kung gayon reverse para dito, ang isang matrix ay isang matrix na tinutukoy A-1 at nagbibigay-kasiyahan sa kondisyon. (Ang kahulugan na ito ay ipinakilala sa pamamagitan ng pagkakatulad sa pagpaparami ng mga numero)