För att integrera rationella funktioner av formen R(sin x, cos x) används en substitution, som kallas den universella trigonometriska substitutionen. Sedan . Universell trigonometrisk substitution resulterar ofta i stora beräkningar. Använd därför följande ersättningar när det är möjligt.

Integrering av funktioner rationellt beroende av trigonometriska funktioner

1. Integraler av formen ∫ sin n xdx , ∫ cos n xdx , n>0
a) Om n är udda, bör en potens av sinx (eller cosx) placeras under tecknet för differentialen, och från den återstående jämna potensen bör man gå till motsatt funktion.
b) Om n är jämnt använder vi reduktionsformlerna
2. Integraler av formen ∫ tg n xdx , ∫ ctg n xdx , där n är ett heltal.
Formler måste användas

3. Integraler av formen ∫ sin n x cos m x dx
a) Låt m och n ha olika paritet. Vi tillämpar substitutionen t=sin x om n är udda eller t=cos x om m är udda.
b) Om m och n är jämna, så använder vi reduktionsformlerna
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Formens integraler
Om talen m och n har samma paritet, så använder vi substitutionen t=tg x . Det är ofta bekvämt att tillämpa tekniken för den trigonometriska enheten.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx
Vi använder formlerna för att omvandla produkten av trigonometriska funktioner till deras summa

Exempel
1. Beräkna integralen ∫ cos 4 x sin 3 xdx .
Vi gör substitutionen cos(x)=t . Då ∫ cos 4 x sin 3 xdx =
2. Beräkna integralen.
Genom att göra substitutionen sin x=t , får vi

3. Hitta integralen.
Vi gör ersättningen tg(x)=t . Vi får ersätta

Observera att ersättningen ctg(x)=t är bekvämare här, sedan dess , och därför

Integration av uttryck av formen R(sinx, cosx)

Exempel #1. Beräkna integraler:

Lösning.
a) Integration av uttryck av formen R(sinx, cosx) , där R är en rationell funktion av sin x och cos x , omvandlas till integraler av rationella funktioner med hjälp av den universella trigonometriska substitutionen tg(x/2) = t .
Då har vi

Den universella trigonometriska substitutionen gör det möjligt att övergå från en integral av formen ∫ R(sinx, cosx) dx till en integral av en rationell-bråk-funktion, men en sådan ersättning leder ofta till krångliga uttryck. På vissa villkor enklare ersättningar visar sig vara effektiva:

• Om likheten R(-sin x, cos x) = -R(sin x, cos x)dx är sann, så tillämpas cos x = t-substitutionen.
• Om R(sin x, -cos x) = -R(sin x, cos x)dx är sant, då är substitutionssin x = t .
• Om R(-sin x, -cos x) = R(sin x, cos x)dx är sant, då är substitutionen tgx = t eller ctg x = t .

I det här fallet, för att hitta integralen
vi tillämpar den universella trigonometriska substitutionen tg(x/2) = t .
Sedan
Eftersom bråket inte är korrekt, då vi markerar heltalsdelen, får vi
Återgå till den ursprungliga variabeln, vi kommer att ha

b) I det andra exemplet, överväg en viktig specialfall, när det allmänna uttrycket ∫ R(sinx, cosx) dx har formen ∫ sin m x cos n xdx . I detta speciella fall, om m är udda, bör substitutionen cos x = t tillämpas. Om n är udda, bör substitutionssin x = t tillämpas. Om båda indikatortyperna är jämna icke-negativa tal (särskilt en av dem kan vara lika med noll), utförs ersättningen enligt de kända trigonometriska formlerna:
I detta fall


Svar:

Grundläggande trigonometriska formler och grundläggande substitutioner presenteras. Metoder för att integrera trigonometriska funktioner beskrivs - integration av rationella funktioner, produkt av potensfunktioner av sin x och cos x, produkt av ett polynom, exponent och sinus eller cosinus, integration av inversa trigonometriska funktioner. Icke-standardiserade metoder påverkas.

Grundläggande trigonometriska formler

Nedan finns några trigonometriska formler som du kan behöva när du integrerar trigonometriska funktioner.

sin 2a + cos 2a = 1






sin(a+b) = sin a cos b + cos a sin b
cos (a+b) = cos a cos b - sin a sin b
sin 2 a = 2 sin a cos a
cos 2 a = cos 2 a - sin 2 a = 2 cos 2 a - 1 = 1 - 2 sin 2 a

Standardsubstitutioner för att integrera trigonometriska funktioner

Här kommer vi att överväga standardsubstitutioner, med hjälp av vilka, i de flesta fall, integreringen av trigonometriska funktioner utförs.

Substitution t = sin x

Transformationen utförs enligt formlerna:

cos x dx = dt;
sin x = t; cos 2 x \u003d 1 - t 2;
;

Substitution t = cos x

sin x dx = - dt;
cos x = t; sin 2 x \u003d 1 - t 2;
;

Substitution t = tg x

; ;
tan x = t; ;
; .

Substitution t = ctg x

; ;
ctg x = t; ;
; .

Substitution t = tg (x/2)

;
;
;
; ;
; .

Integration av inversa trigonometriska funktioner

Integraler som innehåller inversa trigonometriska funktioner
arcsin φ, arctg φ, etc., där φ är någon algebraisk funktion av x , integreras ofta av delar, sätter u = arcsin φ, u = arctg φ, etc.

Exempel på sådana integraler:
, , .

Standardmetoder för att integrera trigonometriska funktioner

Allmän riktlinje

Först, om nödvändigt, måste integranden transformeras så att de trigonometriska funktionerna beror på ett argument, som skulle sammanfalla med integrationsvariabeln.

Till exempel om integranden beror på sin(x+a) och cos(x+b), då bör du utföra omvandlingen:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + sin(x+a) sin(b-a).
Gör sedan ändringen z = x+a . Som ett resultat kommer de trigonometriska funktionerna endast att bero på integrationsvariabeln z .

När trigonometriska funktioner är beroende av ett argument, sammanfallande med integrationsvariabeln (låt oss säga att detta är z ), det vill säga integranden består endast av funktioner av typen synd z, för z, tgz, ctgz, då måste du göra ett byte
.
En sådan substitution leder till integrering av rationella eller irrationella funktioner (om det finns rötter) och gör att man kan beräkna integralen om den är integrerad i elementära funktioner.

Däremot kan du ofta hitta andra metoder som gör att du kan beräkna integralen på ett kortare sätt, baserat på detaljerna i integranden. Nedan är en sammanfattning av de viktigaste sådana metoderna.

Metoder för att integrera rationella funktioner av sin x och cos x

Rationella funktioner från synd x och för xär funktioner som härrör från synd x, för x och alla konstanter som använder operationerna addition, subtraktion, multiplikation, division och höjning till en heltalspotens. De betecknas enligt följande: R (sinx, cosx). Detta kan också inkludera tangenter och cotangenter, eftersom de bildas genom att dividera en sinus med en cosinus och vice versa.
Integraler av rationella funktioner har formen:
.

Metoder för att integrera rationella trigonometriska funktioner är som följer.
1) Substitution leder alltid till en integral av en rationell bråkdel. Men i vissa fall finns det substitutioner (se nedan) som ger kortare beräkningar.
2) Om R (sinx, cosx) cos x → - cos x synd x.
3) Om R (sinx, cosx) multiplicerat med -1 vid byte sin x → - sin x, då substitutionen t = för x.
4) Om R (sinx, cosx)ändras inte som vid samtidig ersättning cos x → - cos x, och sin x → - sin x, då substitutionen t = tg x eller t= ctg x.

Exempel:
, , .

Produkt av potensfunktioner av cos x och sin x

Formens integraler

är integraler av rationella trigonometriska funktioner. Därför är metoderna som beskrivs i föregående avsnitt. Nedan överväger vi metoder baserade på detaljerna hos sådana integraler.

Om m och n rationella nummer, då en av substitutionerna t = synd x eller t= för x integralen reduceras till integralen av differentialbinomialen.

Om m och n är heltal, utförs integrationen med hjälp av reduktionsformlerna:

;
;
;
.

Exempel:
.

Integraler från produkten av ett polynom och en sinus eller cosinus

Formens integraler:
, ,
där P(x) är ett polynom i x är integrerade av delar. Detta resulterar i följande formler:

;
.

Exempel:
, .

Integraler från produkten av ett polynom, exponent och sinus eller cosinus

Formens integraler:
, ,
där P(x) är ett polynom i x, integreras med Euler-formeln
e iax = cos yxa + isin yxa(där i 2 = - 1 ).
För detta beräknar metoden som beskrivs i föregående stycke integralen
.
Efter att ha separerat de verkliga och imaginära delarna från resultatet erhålls de ursprungliga integralerna.

Exempel:
.

Icke-standardiserade metoder för att integrera trigonometriska funktioner

Nedan finns ett antal icke-standardiserade metoder som låter dig utföra eller förenkla integrationen av trigonometriska funktioner.

Beroende av (a sin x + b cos x)

Om integranden endast beror på a sin x + b cos x, är det användbart att tillämpa formeln:
,
var .

till exempel

Nedbrytning av bråk från sinus och cosinus till enklare bråk

Tänk på integralen
.
Det enklaste sättet att integrera är att dekomponera bråket till enklare, genom att tillämpa transformationen:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Integration av bråkdelar av första graden

Vid beräkning av integralen
,
det är bekvämt att välja heltalsdelen av bråket och derivatan av nämnaren
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
Konstanterna A och B hittas genom att jämföra vänster och höger sida.

Referenser:
N.M. Gunther, R.O. Kuzmin, Samling av problem i högre matematik, Lan, 2003.

Betrakta integraler där integranden är produkten av sinus och cosinus av den första graden av x multiplicerat med olika faktorer, det vill säga integraler av formen

Använd de välkända trigonometriska formlerna

(2)
(3)
(4)
man kan omvandla var och en av produkterna i integraler av formen (31) till en algebraisk summa och integrera med formlerna

(5)

(6)

Exempel 1 Hitta

Lösning. Enligt formel (2) kl

Exempel 2 Hitta integral av trigonometrisk funktion

Lösning. Enligt formel (3) kl

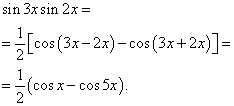
Exempel 3 Hitta integral av trigonometrisk funktion

Lösning. Enligt formel (4) kl vi får följande transformation av integranden:

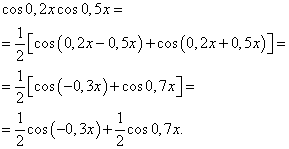
Genom att tillämpa formel (6) får vi

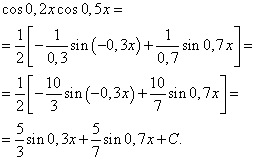
Integral av produkten av potenser av sinus och cosinus av samma argument

Låt oss nu betrakta integralerna av funktioner som är produkten av potenserna av sinus och cosinus av samma argument, dvs.

(7)

I särskilda fall kan en av indikatorerna ( m eller n) kan vara noll.

När man integrerar sådana funktioner används det att den jämna styrkan av cosinus kan uttryckas i termer av sinus och differentialen för sinus lika med cos x dx(eller en jämn potens av sinus kan uttryckas i termer av cosinus, och cosinusdifferentialen är - sin x dx ) .

Två fall bör särskiljas: 1) minst en av indikatorerna m och n udda; 2) båda indikatorerna är jämna.

Låt det första fallet äga rum, nämligen exponenten n = 2k+ 1 - udda. Då med tanke på det

Integranden presenteras på ett sådant sätt att en del av den är en funktion av endast sinus, och den andra är sinusens differential. Nu med byte av variabel t= synd x lösningen reduceras till att integrera polynomet med avseende på t. Om bara examen mär udda, gör sedan detsamma, separerar faktorn synd x, uttrycker resten av integranden i termer av cos x och antar t= cos x. Detta tillvägagångssätt kan också användas när integration av partiella potenser av sinus och cosinus , när åtminstone en av indikatorerna är udda . Hela poängen är den kvoten av potenserna sinus och cosinus är ett specialfall av deras produkt : när den trigonometriska funktionen är i integrandens nämnare är dess grad negativ. Men det finns också fall av partiella trigonometriska funktioner, när deras grader bara är jämna. Om dem - nästa stycke.

Om båda indikatorerna m och när jämna och använder sedan trigonometriska formler

sänk exponenterna för sinus och cosinus, varefter en integral av samma typ som ovan erhålls. Därför bör integrationen fortsätta på samma sätt. Om en av de jämna indikatorerna är negativ, det vill säga kvoten av jämna potenser av sinus och cosinus beaktas, är detta schema inte lämpligt . Sedan används en förändring av variabel, beroende på hur integranden kan transformeras. Ett sådant fall kommer att behandlas i nästa avsnitt.

Exempel 4 Hitta integral av trigonometrisk funktion

Lösning. Exponenten för cosinus är udda. Föreställ dig därför

t= synd x(sedan dt= cos x dx ). Då får vi

För att återgå till den gamla variabeln hittar vi äntligen

Exempel 5 Hitta integral av trigonometrisk funktion

.

Lösning. Exponenten för cosinus, som i föregående exempel, är udda, men mer. Tänka

och gör ändringen av variabeln t= synd x(sedan dt= cos x dx ). Då får vi

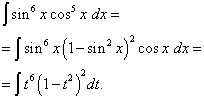
Låt oss öppna parenteserna

och få

Om vi ​​återgår till den gamla variabeln får vi lösningen

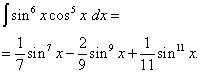
Exempel 6 Hitta integral av trigonometrisk funktion

Lösning. Exponenterna för sinus och cosinus är jämna. Därför transformerar vi integranden enligt följande:

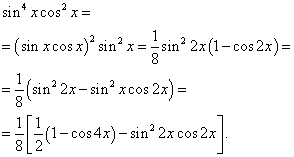
Då får vi

I den andra integralen gör vi en förändring av variabel, inställning t= synd2 x. Sedan (1/2)dt= cos2 x dx . Därmed,

Äntligen får vi

Använda Variable Replace Method

Variabel ersättningsmetod när man integrerar trigonometriska funktioner, kan den användas i fall där endast en sinus eller endast en cosinus finns i integranden, produkten av sinus och cosinus, där antingen sinus eller cosinus är i första graden, tangent eller cotangens, också som kvoten av jämna potenser av sinus och cosinus för ett och samma argument. I det här fallet är det möjligt att utföra permutationer inte bara synd x = t och synd x = t, men även tg x = t och ctg x = t .

Exempel 8 Hitta integral av trigonometrisk funktion

.

Lösning. Låt oss ändra variabeln: , sedan . Den resulterande integranden integreras enkelt över tabellen med integraler:

.

Exempel 9 Hitta integral av trigonometrisk funktion

Lösning. Låt oss konvertera tangenten till förhållandet mellan sinus och cosinus:

Låt oss ändra variabeln: , sedan . Den resulterande integranden är bordintegral med minustecken:

.

För att återgå till den ursprungliga variabeln får vi slutligen:

.

Exempel 10 Hitta integral av trigonometrisk funktion

Lösning. Låt oss ändra variabeln: , sedan .

Vi transformerar integranden för att tillämpa den trigonometriska identiteten :

Vi gör en förändring av variabeln och glömmer inte att sätta ett minustecken framför integralen (se ovan, vad är lika med dt). Därefter delar vi upp integranden i faktorer och integrerar enligt tabellen:

För att återgå till den ursprungliga variabeln får vi slutligen:

.

Hitta integralen av den trigonometriska funktionen själv och se sedan lösningen

Universell trigonometrisk substitution

Universell trigonometrisk substitution kan användas i de fall integranden inte faller under de fall som diskuterats i föregående stycken. I grund och botten när sinus eller cosinus (eller båda) är i nämnaren för ett bråk. Det är bevisat att sinus och cosinus kan ersättas med ett annat uttryck som innehåller tangenten för halva den ursprungliga vinkeln enligt följande:

Men observera att den universella trigonometriska substitutionen ofta medför ganska komplexa algebraiska transformationer, så den används bäst när ingen annan metod fungerar. Låt oss titta på exempel när, tillsammans med den universella trigonometriska substitutionen, substitution under differentialens tecken och metoden för obestämda koefficienter används.

Exempel 12. Hitta integral av trigonometrisk funktion

.

Lösning. Lösning. Låt oss använda universell trigonometrisk substitution. Sedan
.

Vi multiplicerar bråken i täljaren och nämnaren med , och tar ut tvåan och sätter den framför heltecknet. Sedan

Integraler av trigonometriska funktioner.
Lösningsexempel

I den här lektionen kommer vi att överväga integralerna av trigonometriska funktioner, det vill säga fyllningen av integralerna kommer att vara sinus, cosinus, tangenter och cotangenter i olika kombinationer. Alla exempel kommer att analyseras i detalj, tillgängliga och förståeliga även för en tekanna.

För att framgångsrikt studera integraler av trigonometriska funktioner måste du vara väl bevandrad i de enklaste integralerna, samt behärska vissa integrationstekniker. Du kan bekanta dig med dessa material på föreläsningarna. Obestämd integral. Lösningsexempel och .

Och nu behöver vi: Tabell över integraler, Derivattabell och Referensbok med trigonometriska formler. Allt undervisningshjälpmedel finns på sidan Matematiska formler och tabeller. Jag rekommenderar att du skriver ut allt. Jag är särskilt uppmärksam på trigonometriska formler, de borde vara framför dina ögon– utan det kommer arbetets effektivitet märkbart att minska.

Men först, om vilka integraler i den här artikeln Nej. Här finns inga integraler av formen, - cosinus, sinus multiplicerat med något polynom (mindre ofta, något med tangent eller cotangens). Sådana integraler är integrerade av delar, och för att lära dig metoden, besök lektionen Integration av delar. Exempel på lösningar Det finns heller inga integraler med "bågar" - bågtangens, bågsinus, etc., de är också oftast integrerade av delar.

När man hittar integraler av trigonometriska funktioner används ett antal metoder:

(4) Använd tabellformeln , den enda skillnaden är att istället för "x" har vi ett komplext uttryck.

Exempel 2

Exempel 3

Hitta obestämd integral.

En klassiker i genren för de som drunknar i ställningen. Som du säkert har märkt finns det ingen integral av tangent och cotangens i tabellen över integraler, men ändå kan sådana integraler hittas.

(1) Vi använder den trigonometriska formeln

(2) Vi för funktionen under differentialens tecken.

(3) Använd tabellintegralen .

Exempel 4

Hitta den obestämda integralen.

Detta är ett exempel för oberoende beslut, komplett lösning och svar - i slutet av lektionen.

Exempel 5

Hitta den obestämda integralen.

Våra nivåer kommer gradvis att öka =).
Lösning först:

(1) Vi använder formeln

(2) Vi använder den grundläggande trigonometriska identiteten , varav det följer att .

(3) Dividera täljaren med nämnaren term för term.

(4) Vi använder egenskapen linjäritet för den obestämda integralen.

(5) Vi integrerar med tabellen.

Exempel 6

Hitta den obestämda integralen.

Detta är ett exempel för självlösning, den fullständiga lösningen och svaret finns i slutet av lektionen.

Det finns också integraler av tangenter och cotangenter, som är i högre makter. Integralen av tangenten i kuben beaktas i lektionen Hur beräknar man arean av en plan figur? Integraler av tangenten (cotangens) i fjärde och femte potenserna kan erhållas på sidan Komplexa integraler.

Minska graden av integranden

Denna teknik fungerar när integranderna är fyllda med sinus och cosinus även grader. Trigonometriska formler används för att minska graden , och , och den sista formeln används oftare i motsatt riktning: .

Exempel 7

Hitta den obestämda integralen.

Lösning:

I princip är det inget nytt här, förutom att vi har tillämpat formeln (sänker graden av integranden). Observera att jag har förkortat lösningen. Allteftersom erfarenhet erhålls kan integralen av hittas muntligt, detta sparar tid och är helt acceptabelt när man avslutar uppdrag. I det här fallet är det tillrådligt att inte skriva regeln , först tar vi verbalt integralen av 1, sedan - av .

Exempel 8

Hitta den obestämda integralen.

Detta är ett exempel för självlösning, den fullständiga lösningen och svaret finns i slutet av lektionen.

Den utlovade gradhöjningen:

Exempel 9

Hitta den obestämda integralen.

Lösning först, kommentarer senare:

(1) Förbered integranden för att tillämpa formeln .

(2) Vi tillämpar faktiskt formeln.

(3) Vi kvadrerar nämnaren och tar konstanten ur integraltecknet. Det skulle kunna göras lite annorlunda, men enligt mig är det bekvämare.

(4) Vi använder formeln

(5) Under den tredje termen sänker vi igen graden, men med hjälp av formeln .

(6) Vi ger liknande termer (här delade jag term för term och gjorde tillägget).

(7) Vi tar faktiskt integralen, linjäritetsregeln och metoden att föra funktionen under differentialens tecken utförs oralt.

(8) Vi kammar svaret.

! I den obestämda integralen kan svaret ofta skrivas på flera sätt.

I det nyss betraktade exemplet kan det slutliga svaret skrivas annorlunda - öppna parenteserna och gör till och med detta innan du integrerar uttrycket, det vill säga följande slut på exemplet är helt acceptabelt:

Det är möjligt att det här alternativet är ännu bekvämare, jag förklarade det precis som jag brukade bestämma mig själv). Här är ett annat typiskt exempel på en oberoende lösning:

Exempel 10

Hitta den obestämda integralen.

Detta exempel löses på två sätt, och du kan få två helt olika svar.(mer exakt kommer de att se helt annorlunda ut, men ur en matematisk synvinkel kommer de att vara likvärdiga). Chansen är stor att du inte kommer att se det mesta rationellt sätt och lider av öppningsparenteser, med andra trigonometriska formler. Mest effektiv lösning ges i slutet av lektionen.

Sammanfattningsvis stycket drar vi slutsatsen att varje integral av formen , var och - även antal, löses genom att sänka graden av integranden.
I praktiken mötte jag integraler med 8 och 10 grader, jag var tvungen att lösa deras hemska hemorrojder genom att sänka graden flera gånger, vilket resulterade i långa, långa svar.

Variabel ersättningsmetod

Som nämnts i artikeln Variabel ändringsmetod i obestämd integral, huvudförutsättningen för att använda ersättningsmetoden är det faktum att integranden innehåller någon funktion och dess derivata:
(funktioner finns inte nödvändigtvis i produkten)

Exempel 11

Hitta den obestämda integralen.

Vi tittar på derivattabellen och lägger märke till formlerna, , det vill säga i vår integrand finns en funktion och dess derivata. Men vi ser att när man differentierar, omvandlas cosinus och sinus ömsesidigt till varandra, och frågan uppstår: hur gör man en förändring av variabel och vad ska man beteckna för - sinus eller cosinus ?! Frågan kan lösas med den vetenskapliga metoden: om vi byter fel kommer det inte att komma något gott ur det.

Allmän riktlinje: i liknande fall måste du ange funktionen som finns i nämnaren.

Vi avbryter lösningen och genomför ett byte

I nämnaren är allt bra med oss, allt beror bara på , nu återstår det att ta reda på vad det kommer att bli.
För att göra detta hittar vi differentialen:

Eller kort och gott:
Från den resulterande jämlikheten, enligt proportionsregeln, uttrycker vi det uttryck vi behöver:

Så:

Nu beror hela integranden bara på och vi kan fortsätta lösningen

Redo. Jag påminner dig om att syftet med ersättningen är att förenkla integranden, i det här fallet handlar allt om integration kraftfunktion enligt tabellen.

Det var inte av en slump att jag målade det här exemplet så detaljerat, detta gjordes för att upprepa och konsolidera lektionsmaterialet. Variabel ändringsmetod i obestämd integral.

Och nu två exempel för en oberoende lösning:

Exempel 12

Hitta den obestämda integralen.

Exempel 13

Hitta den obestämda integralen.

Kompletta lösningar och svar i slutet av lektionen.

Exempel 14

Hitta den obestämda integralen.

Även här, i integranden, finns en sinus med en cosinus (en funktion med en derivata), men redan i produkten, och ett dilemma uppstår - vad ska betecknas för, sinus eller cosinus?

Du kan försöka göra en ersättning med den vetenskapliga pokemetoden, och om inget fungerar, ange det som en annan funktion, men det finns:

Allmän riktlinje: för du behöver ange den funktion som bildligt talat är i en "obekväm position".

Det ser vi i detta exempel cosinuseleven ”lider” av examen och sinusen sitter fritt sådär, för sig själv.

Så låt oss göra ett byte:

Om någon fortfarande har svårt med variabeländringsalgoritmen och att hitta differentialen, bör du återgå till lektionen Variabel ändringsmetod i obestämd integral.

Exempel 15

Hitta den obestämda integralen.

Vi analyserar integranden, vad ska betecknas med ?
Låt oss ta en titt på våra riktlinjer:
1) Funktionen ligger mest sannolikt i nämnaren;
2) Funktionen är i ett "obekvämt läge".

Förresten, dessa riktlinjer gäller inte bara för trigonometriska funktioner.

Under båda kriterierna (särskilt under det andra) passar sinus, så en ersättning föreslår sig själv. I princip kan bytet redan genomföras, men först skulle det vara trevligt att komma på vad man ska göra med? Först "stiftar" vi en cosinus:

Vi reserverar oss för vår "framtida" differential

Och vi uttrycker genom sinus med den grundläggande trigonometriska identiteten:

Nu här är ersättaren:

Allmän regel: Om en av de trigonometriska funktionerna (sinus eller cosinus) är in i integranden udda grad, då måste du "bita av" en funktion från den udda graden, och utse en annan funktion bakom. Vi talar bara om integraler, där det finns cosinus och sinus.

I det aktuella exemplet hade vi en cosinus i en udda grad, så vi klämde bort en cosinus från graden och betecknade sinus.

Exempel 16

Hitta den obestämda integralen.

Nivåerna går upp =).
Det här är ett gör-det-själv-exempel. Komplett lösning och svaret i slutet av lektionen.

Universell trigonometrisk substitution

Universell trigonometrisk substitution är ett vanligt fall av byte av variabel metod. Du kan försöka tillämpa det när du "inte vet vad du ska göra." Men i själva verket finns det några riktlinjer för dess tillämpning. Typiska integraler där den universella trigonometriska substitutionen måste tillämpas är följande integraler: , , , etc.

Exempel 17

Hitta den obestämda integralen.

Den universella trigonometriska substitutionen i detta fall implementeras på följande sätt. Låt oss ersätta: . Jag använder inte bokstaven, men bokstaven, det här är inte någon form av regel, bara igen, jag är så van att bestämma mig.

Här är det mer bekvämt att hitta skillnaden, för detta, från jämlikheten, uttrycker jag:
Jag hänger på båda delarna av bågtangensen:

Arctangens och tangent tar bort varandra:

På det här sättet:

I praktiken kan du inte måla så detaljerat, utan helt enkelt använda det färdiga resultatet:

! Uttrycket är endast giltigt om vi under sinus och cosinus bara har "xes", för integralen (som vi kommer att prata om senare) allt blir lite annorlunda!

När vi byter ut sinus och cosinus förvandlas vi till följande bråk:
, , dessa likheter är baserade på välkända trigonometriska formler: ,

Så städningen kan se ut så här:

Låt oss utföra en universell trigonometrisk substitution: