Lektionspresentation: "Stereometri". Grunderna i stereometri Presentation om ämnet stereometri axiom

Bild 1

Metodisk utveckling Savchenko E.M. MOU gymnasium №1, Polyarnye Zori, Murmansk-regionen.
Ämne för stereometri
Stereometri axiom
Geometri årskurs 10

Bild 2

Planimetri
Stereometri
Utforskar egenskaperna hos geometriska former på ett plan
Utforskar egenskaperna hos former i rymden
Översatt från grekiska betyder ordet "geometri" "mätning" "geo" - i grekiskt land, "metreo" - att mäta
Ordet "stereometri" kommer från de grekiska orden "stereos" volumetrisk, rumslig, "metero" - att mäta

Bild 3

Planimetri
Stereometri
Tillsammans med dessa figurer kommer vi att överväga geometriska kroppar och deras ytor. Till exempel polyedrar. Kub, parallellepiped, prisma, pyramid. Roterande kroppar. Kula, klot, cylinder, kon.
Grundläggande former: punkt, linje
Grundläggande former: punkt, linje, plan
Andra former: segment, stråle, triangel, kvadrat, romb, parallellogram, trapets, rektangel, konvexa och icke-konvexa n-goner, cirkel, cirkel, båge, etc.

Bild 4

För att ange punkter använder vi stora latinska bokstäver
För beteckningen av raka linjer använder vi små latinska bokstäver.
Eller så betecknar vi en rak linje med två latinska versaler.

Bild 5

Planen kommer att betecknas med grekiska bokstäver.
I figurerna är planen indikerade i form av parallellogram. Ett plan som en geometrisk figur bör tänkas sträcka sig oändligt åt alla håll.

Bild 6

Bild 7

När du studerar rumsliga figurer, i synnerhet geometriska kroppar, använd deras platta bilder i ritningen. Bilden av en rumslig figur är dess projektion på ett visst plan. Samma figur tillåter olika bilder.
Olika konbilder

Bild 8

Stereometri används ofta inom konstruktion, arkitektur, maskinteknik, geodesi och inom många andra områden inom vetenskap och teknik.
När man konstruerade denna maskin var det viktigt att få en sådan form så att luftmotståndet var minimalt vid förflyttning.

Bild 9

Operahuset i Sydney
Den danske arkitekten Jorn Utzon inspirerades av synen av seglen.

Bild 10

Eiffeltornet Paris, Champ de Mars
Ingenjören Gustave Eiffel hittade en ovanlig form för sitt projekt. Eiffeltornet är mycket robust: en stark vind avleder sin topp med endast 10-12 cm. I värmen, från ojämn uppvärmning av solens strålar, kan den avvika med 18 cm.

Bild 11

18 000 järndelar är fästa med 2 500 000 nitar

Bild 12

Den ursprungliga idén för byggandet av tornet hittades av arkitekterna L. Batalov och D. Burdin med deltagande av designern N. Nikitin. Metallkablar sträcks inuti de cylindriska betongblocken. Denna design är extremt stabil.
Den teoretiska nedböjningen av torntoppen vid maximala designade vindhastigheter är cirka 12 meter.

Bild 13

De grundläggande egenskaperna hos punkter, linjer och plan uttrycks i axiom. Vi kommer bara att formulera tre av de många axiomen.
A1. Genom tre valfria punkter som inte ligger på en rak linje passerar ett plan, och dessutom bara en.
Illustration för Axiom A1: glasplattan kommer att ligga tätt på tre punkter A, B och C, som inte ligger på en rak linje.
A
B
C

Bild 14

Illustrationer till A1 axiom från livet.
Den trebenta pallen kommer alltid att sitta perfekt på golvet och svajar inte. En fyrbent pall har stabilitetsproblem om benen på pallen inte är lika långa. Pallen svajar, det vill säga den vilar på tre ben, och det fjärde benet (den fjärde "punkten") ligger inte i golvets plan, utan hänger i luften.
För en videokamera, fotografering och andra enheter används ofta ett stativ. Stativets tre ben kommer stabilt att passa alla inomhusgolv, på asfalten eller direkt på gräsmattan utomhus, på sanden på stranden eller i gräset i skogen. De tre stativbenen hittar alltid ett plan.

Bild 15

O
A
V
Rita räta vinklar på marken med en enkel enhet som kallas en ecker.
Stativ med ecker.

Bild 16

a
A2. Om två punkter på en rät linje ligger i ett plan, så ligger alla punkter på en rät linje i detta plan.
A
B

Bild 17

Egenskapen uttryckt i A2-axiomet används för att kontrollera "jämnheten" för ritningslinjalen. Linjalen appliceras med sin kant mot bordets plana yta. Om linjalens kant är jämn, gränsar den med alla dess spetsar till bordsytan. Om kanten är ojämn, bildas på vissa ställen ett gap mellan den och bordsytan.

Bild 18

Axiom A2 innebär att om en rät linje inte ligger i ett givet plan, så har den högst en gemensam punkt med sig. Om en linje och ett plan bara har en punkt gemensamt, så säger de att de skär varandra.

Bild 19

a
A3. Om två plan har en gemensam punkt, så har de en gemensam rät linje på vilken alla de gemensamma punkterna för dessa plan ligger.
I det här fallet sägs planen skära varandra i en rak linje.

Bild 20

Axiom A3 illustreras tydligt av skärningspunkten mellan två intilliggande väggar, en vägg och ett tak i ett klassrum.

Bild 21

A1. Genom tre valfria punkter som inte ligger på en rak linje passerar ett plan, och dessutom bara en.

Bild 22

Sats
Ett plan passerar genom en rak linje och en punkt som inte ligger på den, och dessutom bara en.
M
a

Bild 23

Några konsekvenser från axiomen.
Sats
Ett plan passerar genom två korsande linjer, och dessutom bara en
M
a
b
N

Bild 24

Träningsövningar
Nämn planen i vilka linjerna ligger PE MK DB AB EC
P
E
A
B
C
D
M
K

Bild 25

Träningsövningar
Nämn skärningspunkterna för den räta linjen DK med planet ABC, den räta linjen CE med planet ADB.
P
E
A
B
C
D

Lektionscykeln om ämnet: "Stereometrins axiom" består av följande lektioner:

1. Ämne för stereometri. Stereometrins axiom"

2. Några avledningar från axiomen.

3; 4. Lösa problem med tillämpningen av axiom och deras konsekvenser.

5. Lösa problem kring tillämpningen av stereometrins axiom och deras konsekvenser. Självständigt arbete.

En presentation har förberetts för varje lektion.

Ladda ner:

Förhandsvisning:

Lektionscykel om ämnet: "Stereometrins axiom och deras konsekvenser."

Lektion 1. Ämne stereometri. Stereometri axiom.

Lektionens mål:

att bekanta eleverna med innehållet i stereometrikursen;
studera axiomen om det inbördes arrangemanget av punkter, linjer och plan i rymden;
att lära sig att tillämpa stereometrins axiom när man löser problem.

Under lektionerna:

Bild 1.

1. Organisatoriskt ögonblick.

2. Att lära sig nytt material.

Lärare: Sedan tre år tillbaka, med start i 7:an, läser vi skolans geometrikurs.

Bild 2. Frågor till studenter:

Vad är geometri? (Geometri är vetenskapen om egenskaperna hos geometriska former)

Vad är planimetri? (Planimetri är en sektion av geometri som studerar egenskaperna hos figurer på ett plan)

Vilka grundläggande begrepp inom planimetri känner du till? (punkt, linje)

Lärare: Idag börjar vi studera ett nytt avsnitt av geometri - stereometri.

Bild 3. Stereometri är en del av geometrin där egenskaperna hos figurer i rymden studeras. (Eleverna skriver i en anteckningsbok)

Bild 4. Grundläggande rymdbegrepp: punkt, linje, plan.

Idén om ett plan ges av den släta ytan på ett bord, vägg, golv, tak, etc. Planet, som en geometrisk figur, måste föreställas sträcka sig i alla riktningar, oändligt. Planen betecknas med de grekiska bokstäverna α, β, γ, etc.

1. Namnge de punkter som ligger i planet β; inte ligger i planet β.

2. Namnge linjerna: liggande i planet β; inte ligger i planet β.

Bild 5. Vi har en visuell representation av de grundläggande begreppen (punkt, linje, plan) och de ges inga definitioner. Deras egenskaper uttrycks i axiom.

Tillsammans med en punkt, en rät linje, ett plan i stereometri, beaktas geometriska kroppar (kub, parallellepiped, cylinder, tetraeder, kon, etc.), deras egenskaper studeras, deras area och volym beräknas. Objekten runt omkring oss ger en uppfattning om geometriska kroppar.

Bild 6. Frågor till studenter:

Vilka geometriska kroppar påminner objekten som avbildas i dessa ritningar dig om?

Namnge objekt i din miljö (vårt klassrum) som påminner dig om geometriska kroppar.

Bild 7. Praktiskt arbete (i anteckningsböcker)

1. Rita en kub i en anteckningsbok (synliga linjer - en heldragen linje, osynlig - en prickad linje).

2. Beteckna kubens hörn med versaler ABCDA 1 B 1 S 1 D 1

3. Markera med en färgpenna:

hörn A, C, B 1, D 1 ; segment AB, SD, B 1 S, D 1 MED; diagonalerna på kvadraten AA 1 I 1 V.

Uppmärksamma eleverna på synliga och osynliga linjer i ritningen; AA fyrkantig bild 1 på 1 I rymden.

Bild 8. Frågor till studenter:

Vad är ett axiom? Vilka planimetriska axiom känner du till?

I rymden uttrycks de grundläggande egenskaperna hos punkter, linjer och plan, angående deras relativa position, i axiom.

Bild 9. Eleverna antecknar och ritar i anteckningsböcker.

Axiom 1. (A1) Genom valfria 3 punkter som inte ligger på en rät linje finns ett plan och dessutom bara en.

Bild 10. Observera att om vi inte tar 3, utan 4 godtyckliga punkter, får inte ett enda plan passera genom dem, det vill säga 4 punkter kanske inte ligger i samma plan.

Bild 11. Axiom 2. (A2) Om 2 punkter på en rät linje ligger i ett plan, så ligger alla punkter på en rät linje också i detta plan. I det här fallet säger de att en rak linje ligger i ett plan eller att ett plan passerar genom en rak linje.

Bild 12. Fråga till eleverna:

Hur många punkter har en linje och ett plan gemensamt? (Fig. 1 - oändligt många; Fig. 2 - en)

Bild 13. Axiom 3. (A3) Om två plan har en gemensam punkt, så har de en gemensam linje på vilken alla de gemensamma punkterna för dessa plan ligger.

I det här fallet sägs planen skära varandra i en rak linje.

3. Konsolidering av det studerade materialet.

Bild 14. Lösa problem från lärobok nr 1 (a, b), 2 (a).

Eleverna läser problemformuleringen och ger med hjälp av bilden på bilden ett svar med en förklaring.

Mål 1.

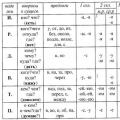
a) P, E (ADV) PE (ADV) enligt A 2

Liknar MK (VDS)

V, D (ADV) och (VDS) VD (ADV) och (ICE)

Liknar AB (ADV) och (ABC)

C, E (ABC) och (DES) CE (ABC) och (DES)

b) C (DK) och (ABC) DK ∩ (ABC) = S. T. till. det finns högst en skärningspunkt mellan en rät linje och ett plan (den räta linjen ligger inte i planet), då är detta den enda punkten.

På samma sätt är CE ∩ (ADV) = E.

Uppgift 2 (a)

I planet DSS 1: D, S, S 1, D 1 , K, M, R. I planet BQC: B 1, B, P, Q, C1, M, C.

Bild 15. 4. Sammanfattning av lektionen.Frågor till studenter:

Vad heter det avsnitt av geometri som vi ska studera i årskurs 10-11?
Vad är stereometri?
Formulera med hjälp av bilden stereometrins axiom som du lärde dig i dagens lektion.

Bild 16. 5. Läxor.

Lektion 2. Några konsekvenser från axiomen.

Lektionens mål:

Gå igenom stereometrins axiom och deras tillämpning för att lösa läxproblem;

Att bekanta eleverna med implikationerna av axiomen;

Att lära ut hur man tillämpar följderna från axiomen vid problemlösning, samt att befästa förmågan att tillämpa stereometrins axiom vid problemlösning;

Upprepa formeln för att beräkna arean av en romb.

Under lektionerna.

Bild 1. 1. Organisatoriskt ögonblick.Kommunikation av ämnet och målen för lektionen.

Bild 2.

1) Formulera stereometrins axiom och rita upp ritningarna på tavlan.

2) nr 1 (c, d); 2 (b, e).

Eleverna svarar muntligt från bilden på bilden på läxfrågorna.

Bild 3. 3. Att lära sig nytt material.Betrakta och bevisa följderna av axiomen.

Sats 1. Ett plan passerar genom en rät linje och en punkt som inte ligger på den, och dessutom bara en.

Eleverna skriver ner ordalydelsen i en anteckningsbok och, som svarar på lärarens frågor, gör lämpliga anteckningar och ritningar i anteckningsboken.

Vad anges i satsen? (rak och icke-liggande punkt)

Vad behöver bevisas? (passerar planet; en)

Vad kan användas för att bevisa? (axiom för stereometri)

Vilket av axiomen låter dig bygga ett plan? (A1, ett plan passerar genom tre punkter och dessutom bara en)

Vad finns i den här satsen och vad saknas för att använda A1 (vi har - en punkt; ytterligare två poäng behövs)

Var ska vi rita två punkter till? (på den här raden)

Vilken slutsats kan vi dra? (bygg ett plan genom tre punkter)

Tillhör detta plan en rak linje? (Ja)

På vilken grund kan en sådan slutsats dras? (baserat på A2: om två punkter på en rät linje tillhör planet, så tillhör hela den räta linjen planet)

Hur många plan kan du rita genom en given linje och en given punkt? (ett)

Varför? (eftersom ett plan passerar genom en rät linje och ett plan passerar genom en given punkt och två punkter på en rät linje, betyder det att längs A1 är detta plan det enda)

Bild 4. Sats 2. Ett plan passerar genom två skärande linjer och dessutom bara en.

Eleverna bevisar satsen på egen hand, lyssnar sedan efter flera bevis och gör tillägg och förfining (om det behövs)

Var uppmärksam på det faktum att beviset inte är baserat på axiom, utan på konsekvens 1.

Bild 5. 4. Konsolidering av det studerade materialet.

Problem 6 (från handledning)

Eleverna arbetar i skrivböcker, föreslår sina egna lösningar och jämför sedan sin lösning med lösningen på skärmen. Två fall analyseras: 1) punkterna ligger inte på en rät linje; 2) punkterna är kolinjära.

Bild 6.7. Uppgiften är på bilden. Eleverna läser villkoret, gör en ritning och gör nödvändiga anteckningar i anteckningsböcker. Läraren bedriver frontarbete med klassen om problemet. När vi löser problemet upprepar vi formlerna för att beräkna arean av en romb.

Givet: AVSD - rhombus, AS∩VD = O, M(A, D, O); AB = 4 cm, A = 60º.

Hitta: (B, C); D (MOU); (MOB) ∩ (ADO); S AVSD.

Lösning:

Var uppmärksam på det faktum att om två plan har gemensamma punkter, så skär de sig i en rak linje som passerar genom dessa punkter.

5. Sammanfattning:

Formulera stereometrins axiom.

Formulera konsekvenserna av axiomen.

Målet med lektionen har uppnåtts. Vi upprepade stereometrins axiom, bekantade oss med konsekvenserna av axiomen och använde dem för att lösa problem.

Markering (med kommentarer)

Bild 8. 6. Göra läxor:

Lektion 3. Lösa problem om tillämpningen av stereometrins axiom och deras konsekvenser.

Lektionens mål:

Gå igenom stereometrins axiom och deras konsekvenser;

Att bilda färdigheten att tillämpa stereometrins axiom och deras konsekvenser vid problemlösning;

Eleverna känner till stereometrins axiom och deras konsekvenser och kan tillämpa dem vid problemlösning.

Under lektionerna.

Bild 1. 1. Organisatoriskt ögonblick.Kommunikation av ämnet och målen för lektionen.

2. Förverkligande av elevernas kunskaper.

1) Kontrollera läxor på elevfrågor.

Före lektionen, ta med läxanteckningsböcker från flera elever för granskning.

2) Två elever förbereder vid tavlan beviset på konsekvenserna av axiomen.

3) Två elever (nivå 1) och två elever (nivå 2) arbetar med individuella undersökningskort. Glida.

4) Frontalarbete med elever.

Bild 2. Givet: kub AVSDA1V1S1D1

Hitta:

Flera punkter som ligger i α-planet; (A, B, C, D)
Flera punkter som inte ligger i α-planet; (A 1, B 1, C 1, D 1)
Flera raka linjer som ligger i planet α; (AB, VS, SD, AD, AS, VD)
Flera linjer som inte ligger i planet α; (A 1 B 1, B 1 C 1, C 1 D 1, A 1 D 1, A 1 C 1, B 1 D 1, AA 1, BB 1, SS 1, DD 1)
Flera raka linjer som skär linjen BC; (BB 1, CC 1)
Flera raka linjer som inte korsar linjen BC. (HELVETE, AA 1 …)

Bild 3. Fyll i de tomma fälten för att få rätt påstående:

Bild 4. Är raka AA 1 , AB, AD i samma plan? (Direkt AA 1 , AB, HELVETE passerar genom punkt A, men ligger inte i samma plan)

3. Lösa problem.

Bild 5. Eleverna löser problem nr 7, 10, 14 från läroboken och gör lämpliga ritningar och anteckningar på tavlan och i anteckningsböcker.

Problem nummer 7.

2) Ligger alla räta linjer som går genom punkten M i samma plan?

Lösning: Genom konsekvens 2:

2) Alla linjer som går genom punkten M ligger inte nödvändigtvis i samma plan. (se exempel från bild 4)

Uppgift 10. Eleverna löser problemet på egen hand (liknar uppgift nummer 7). Läraren tar selektivt anteckningsböcker för kontroll och ger individuell hjälp med att lösa problemet till elever som inte orkade med uppgiften.

Problem nummer 14. Lösning: Alla linjer a, b, c ligger i samma plan. I det här fallet, med konsekvens 2, kan ett plan ritas, och ett plan passerar genom tre räta linjer.

En av de tre räta linjerna, till exempel c, ligger inte i planet α som definieras av räta linjer a och b. I detta fall passerar tre olika plan genom de givna tre räta linjerna, definierade av par av räta linjer a och b, a och c, b och c.

Bild 6. Eleverna gör en ritning och nödvändiga konstruktioner och anteckningar i anteckningsböcker. När man bygger uttalar eleverna axiomen, resultatet av konstruktionen skrivs med hjälp av symboler.

Uppgift. Givet: kub AVSDA 1 B 1 C 1 D 1

tM ligger på kanten BB 1 , punkt N ligger på kanten CC 1 och punkt K ligger på kanten DD 1

a) Nämn planen där punkterna M ligger; N.

b) hitta punkten F-punkten för skärningspunkten mellan linjerna МN och BC. Vilken egenskap har punkt F?

c) hitta skärningspunkten för den räta linjen KN och planet ABC.

d) hitta skärningslinjen för planen MNK och ABC.

Lösning:

Bild 7. För att lösa nästa problem upprepar vi formeln för att beräkna arean av en fyrkant. Härledningen av formeln analyseras över bilden.

Eleverna skriver ner formeln i en anteckningsbok.

Bild 8. Bevisa att alla hörn på AVSD-fyrhörningen ligger i samma plan om dess diagonaler AC och VD skär varandra.

Beräkna arean av fyrkanten, om AS┴VD, AS = 10cm, VD = 12cm.

Svar: 60 cm 2

4. Sammanfattning av lektionen.

Vad orsakade svårigheten? Läraren tillkännager betygen på lektionen med en kommentar.

Bild 9.

Lektion 4. Lösa problem om tillämpningen av stereometrins axiom och deras konsekvenser.

Lektionens mål:

Styra kunskapen om stereometrins axiom och deras konsekvenser;

Att befästa den formade färdigheten att tillämpa stereometrins axiom och deras konsekvenser vid problemlösning;

Granskning: Pythagoras sats och dess tillämpning; formler för att beräkna arean av en liksidig triangel, rektangel.

Under lektionerna.

Bild 1. 1. Organisatoriskt ögonblick.Kommunikation av ämnet och målen för lektionen.

Bild 2. 2. Kontrollera läxor.

Före lektionen, ta med läxanteckningsböcker från flera elever för granskning.

Två elever förbereder vid tavlan lösningar på problem från läxor - nr 9, 15.

Resten av eleverna svarar på frågorna i matematikdiktatet på bilden.

Bild 3. 3. Problemlösning (frontalarbete med klassen)

Problem nummer 1.

Du får en MABS-tetraeder, vars kant är 6 cm.

Nämn linjen längs vilken planen skär: a) MAB och MFC; b) MCF och ABC.
Hitta längden på СF och SАВС
Hur bygger man skärningspunkten för den räta linjen DE med planet ABC?

Frågor till studenter (vid behov):

Vilka punkter tillhör båda planen samtidigt. Vilket axiom kan användas för att dra en slutsats?

Ange egenskapen för medianen för en likbent triangel.

Formulera Pythagoras sats.

Varför kan vi tillämpa Pythagoras sats i detta fall?

Vilka metoder kan användas för att beräkna arean av en liksidig triangel?

Är det alltid möjligt att bygga skärningspunkten för den räta linjen MU med planet ABC?

Bild 4. Problem nummer 2.

Hur man bygger skärningspunkten för planet ABC med den räta linjen D 1 R?
Hur man ritar en skärningslinje för blodtrycksplanet 1 P och ABB 1?
Beräkna längden på segmenten AR och BP 1 om AB = a

Lösning:

Bild 5. Problem nummer 3.

Given : Punkterna A, B, C ligger inte på en rak linje.

Bevisa att punkten P ligger i planet ABC.

Med hjälp av animering på bilden drar eleverna lämpliga konstruktioner och nödvändiga slutsatser. De gör anteckningar i anteckningsböcker med hjälp av matematiska symboler, uttalar motsvarande axiom och konsekvenser från axiomen.

Frågor till studenter (efter behov):

Vet man att punkterna A, B, C inte ligger på en rät linje, vilken slutsats kan man dra?

Om punkterna A och B ligger i planet, vilken slutsats kan man dra om linjen AB?

Vilken slutsats kan dras om punkten M?

Om punkterna A och C ligger i planet, vilken slutsats kan man dra om linjen AC?

Vilken slutsats kan dras om punkten K?

Med vetskap om att punkterna M och K ligger i planet, vilken slutsats kan man dra om den räta linjen MK?

Vilken slutsats kan dras om punkten P?

Lösning (ett annat sätt att bevisa):

AB∩AC = A. Enligt den andra följden definierar räta linjer AB och AC planet α. Punkt M tillhör AB, vilket betyder att den tillhör planet α, och punkt K tillhör AC, och därför också till planet α. Enligt axiom A2: MK ligger i planet α. Punkten P tillhör MC, och därmed till planet α.

Bild 6. Problem nummer 4.

Planen α och β skär i en rät linje med. Linje a ligger i planet α och skär planet β. Skär linjerna a och c? Varför?

Frågor till studenter (vid behov):

Vet man att den räta linjen a skär planet β, vilken slutsats kan man dra? (En rät linje och ett plan har en gemensam punkt, till exempel punkt B)

Vilken egenskap har punkt B? (Punkt B tillhör linje a, plan α och plan β)

Om en punkt tillhör två plan samtidigt, vad kan vi då säga om planens relativa position? (plan skär i en rät linje, till exempel med)

Vilken är den relativa positionen för punkt B och linje c? (punkt B tillhör linje c)

Med vetskapen om att punkt B tillhör både linje a och linje c, vilken slutsats kan man dra om dessa linjer? (linjer skär varandra i punkt B)

Bild 7. Problem nummer 5.

Givet en rektangel AVSD är O skärningspunkten för dess diagonaler. Det är känt att punkterna A, B, O ligger i planet α. Bevisa att punkterna C och D också ligger i planet α. Beräkna arean av rektangeln om AC = 8 cm, AOB = 60º.

Uppgiften är avsedd för en självständig lösning med diskussion om lösningen och tillhandahållande av individuell hjälp till elever. Det är bra att diskutera olika sätt att hitta arean av en rektangel:

Be eleverna att lösa problemet på olika sätt. Svar: 16 cm 2.

4. Sammanfattning av lektionen:

Vilka axiom och satser använde vi i lektionen när vi löste problem? Formulera.

Vilka uppgifter var de mest intressanta, de svåraste?

Vad var användbart för dig personligen på lektionen?

Vad orsakade svårigheten?

Märkning för lektionen (med kommentar till varje märke)

Bild 8. 5. Göra läxor:

Lektion 5. Lösa problem om tillämpningen av stereometrins axiom och deras konsekvenser. Självständigt arbete (20 min.)

Lektionens mål:

Att konsolidera assimileringen av teoretiska frågor i processen att lösa problem;

Kontrollera elevernas beredskapsnivå genom att bedriva självständigt arbete av kontrollerande karaktär.

Under lektionerna.

Bild 1. 1. Organisatoriskt ögonblick.

Kommunikation av ämnet och målen för lektionen.

Bild 2. 2. Kontrollera läxor.

Före lektionen, ta med läxanteckningsböcker från flera elever för granskning.

Mål 1.

Linjerna a och b skär varandra i punkt O, A a, B b, P AB. Bevisa att linjerna a och b och punkt P ligger i samma plan.

Lösning:

Bild 3. Uppgift 2.

I denna figur innehåller planet α punkterna A, B, C, D, men innehåller inte punkten M. Konstruera punkt K - skärningspunkten mellan linjen AB och planet MSD. Ligger punkt K i planet α.

Lösning:

Bild 4, 5, 6 3. Verbal lösning av problem för teorirevision (genom bilder)

Slides 7.8 4. Självständigt arbete(flernivåer, kontrollerande natur) Eleverna väljer sin svårighetsgrad.

5. Sammanfattning.

1) Samla anteckningsböcker med självständigt arbete.

2) Kungörelse av märken med kommentarer.

Bild 9. 6. Läxor.

Förhandsvisning:

För att använda förhandsvisningen av presentationer, skapa dig ett Google-konto (konto) och logga in på det: https://accounts.google.com

Bildtexter:

Lektion 1 Ämne: "Ämne för stereometri. Axiom för stereometri."

Vad är geometri? Geometri - vetenskapen om egenskaperna hos geometriska former "Geometri" - (grekiska) - "lantmäteri" - Vad är planimetri? Planimetri är en del av geometrin där egenskaperna hos figurer på ett plan studeras. Och a Grundläggande begrepp för planimetri: punkt är en rät linje - Grundläggande begrepp för planimetri?

Stereometri - en sektion av geometri där egenskaperna hos figurer i rymden studeras

Grundsiffror i rymden: punkt rakt plan α β Beteckning: А; V; MED; ...; М;… a А В М N Р Beteckning: a, b, c, d ..., m, n, ... (eller med två versaler på latin) Beteckning: α, β, γ ... Svara på frågor i figuren: 1. Namnge punkterna som ligger i planet β; inte ligger i planet β. 2. Vilka linjer ligger i planet β; inte ligger i planet β

Några geometriska kroppar. A B C D D 1 C 1 B 1 A 1 kub A B C D A 1 B 1 C 1 D 1 parallellepiped A B C D tetraedercylinderkon

Namnge vilka geometriska kroppar som påminner dig om objekten som avbildas i dessa figurer: Namnge objekten från din miljö (vårt klassrum) som påminner dig om geometriska kroppar.

Praktiskt arbete. 1. Rita en kub i en anteckningsbok (synliga linjer - en heldragen linje, osynlig - en prickad linje). 2. Beteckna kubens hörn med versaler ABCDA 1 B 1 C 1 D 1 ABCDD 1 C 1 B 1 A 1 3. Välj med en färgpenna: hörn A, C, B 1, D 1 segment AB, SD, B 1 С, Д 1 С kvadratisk diagonal АА 1 В 1 В

Vad är ett axiom? Ett axiom är ett uttalande om egenskaperna hos geometriska figurer, taget som utgångspunkt, utifrån vilket satser bevisas ytterligare och i allmänhet är all geometri konstruerad. Planimetriska axiom: - genom två valfria punkter kan du dra en rak linje och dessutom bara en. av tre punkter, en rak linje, och endast en, ligger mellan de andra två. det finns minst tre punkter som inte ligger på en rak linje ...

Stereometri axiom. A B C A1. Genom tre valfria punkter som inte ligger på en rak linje passerar ett plan och dessutom bara en. α

Om bordets ben inte är lika långa, så står bordet på tre ben, d.v.s. vilar på tre "punkter", och änden av det fjärde benet (fjärde punkten) ligger inte i golvets plan, utan hänger i luften.

Stereometri axiom. А В α А2. Om två punkter på en rät linje ligger i ett plan, så ligger alla punkter på denna räta linje i detta plan. De säger: en rät linje ligger i ett plan eller ett plan passerar genom en rät linje.

a M Den räta linjen ligger i planet Den räta linjen skär planet Hur många punkter har linjen och planet gemensamma?

Stereometri axiom. αβ A3. Om två plan har en gemensam punkt, så har de en gemensam rät linje på vilken alla de gemensamma punkterna för dessa plan ligger. De säger: plan skär varandra i en rak linje. ah

Lös problem: №1 (a, b); 2 (a) A B S D R E K M A B S D A 1 B 1 C 1 D 1 Q P R K M Namn enligt figuren: a) de plan i vilka de räta linjerna DV, AB, MK, PE, EC ligger; b) skärningspunkten för den räta linjen DC med planet ABC, den räta linjen CE med planet ADV. a) punkter som ligger i planen DSS 1 och B Q C nr 1 (a, b) nr 2 (a)

Låt oss sammanfatta lektionen: 1) Vad heter geometridelen som vi ska studera i årskurs 10-11? 2) Vad är stereometri? 3) Formulera med hjälp av bilden stereometrins axiom som du lärde dig på lektionen idag. А А В В α α А α β

Sats 1. Ett plan passerar genom en rät linje och en punkt som inte ligger på den, och dessutom bara en. Givet: a, M ¢ a Bevisa: (a, M) med α α är det enda M α-beviset: 1. P, O med a; (P, O, M) ¢ a P O Enligt A1-axiomet: ett plan passerar genom punkterna P, O, M. Enligt Axiom A2: sedan två punkter på en rät linje tillhör ett plan, då hör hela den räta linjen till detta plan, d.v.s. (a, M) med α2. Varje plan som passerar genom en rät linje a och en punkt M passerar genom punkterna P, O och M, vilket betyder, enligt A1-axiomet, att det är det enda. Ch.t.d. Några konsekvenser från axiomen:

Sats 2. Ett plan passerar genom två skärande linjer, och dessutom bara en. Givet: a ∩ b Bevisa: 1. (a∩ b) c α 2. α är det enda a b M H α Bevis: 1. Planet α passerar genom a och H a, H b. (M, H) α, (M, H) b, så vid A2 hör alla punkter b till planet. 2. Planet passerar genom a och b och det är det enda, sedan vilket plan som helst som går genom linjerna a och b går också genom H, vilket betyder att α är den enda.

Lös problem nummer 6 А В С α Tre givna punkter är kopplade parvis med segment. Bevisa att alla linjesegment ligger i samma plan. Bevis: 1. (A, B, C) α, så längs A1 till A, B, C passerar det enda planet. 2. Två punkter av varje segment ligger i planet, därför, enligt A2, ligger alla punkter för vart och ett av segmenten i planet α. 3. Slutsats: AB, BC, AC ligger i planet α 1 fall. A B C α 2 fall. Bevis: Eftersom 3 punkter tillhör en rät linje, så ligger enligt A2 alla punkter på denna räta linje i planet.

Uppgift. А В С Д М О AVSD - romb, O - skärningspunkt för dess diagonaler, M - rymdpunkt som inte ligger i rombens plan. Punkterna A, D, O ligger i planet α. Bestäm och motivera: Ligger punkterna B och C i planet α? Ligger punkt D i MOV-planet? Namnge skärningslinjen för MOV- och ADO-planen. Beräkna arean av en romb om dess sida är 4 cm och vinkeln är 60º. Föreslå olika sätt att beräkna arean av en romb.

Muntligt arbete. A B S D A 1 B 1 C 1 D 1 α Givet: kub ABSDA 1 B 1 C 1 D 1 Hitta: Flera punkter som ligger i planet α; Flera punkter som inte ligger i α-planet; Flera raka linjer som ligger i planet α; Flera linjer som inte ligger i planet α; Flera raka linjer som skär linjen BC; Flera raka linjer som inte korsar linjen BC. Mål 1.

Muntligt arbete. Uppgift 2. α А М В а b c Fyll i de tomma fälten för att få rätt påstående:

Muntligt arbete. A B C D A 1 B 1 C 1 D 1 α Linjerna AA 1, AB, HELVETE går genom punkt A, men ligger inte i samma plan Ligger linjerna AA 1, AB, HELVETE i samma plan?

Lös problemen från handledningen: s. 8 № 7, 10, 14. Elevernas arbete på tavlan och i anteckningsböcker:

Uppgift 1 A B C D A 1 B 1 C 1 D 1 M NF K Givet: kuben ABCDA 1 B 1 C 1 D 1 tM ligger på kanten BB 1, dvs N ligger på kanten CC 1 och punkten K ligger på kanten DD 1 a ) namnge de plan i vilka punkterna M ligger; N. b) hitta punkten F-punkten för skärningspunkten mellan linjerna M N och BC. Vilken egenskap har punkt F? c) hitta skärningspunkten för den räta linjen K N och planet ABC O d) hitta skärningslinjen för planen M N K och ABC

Problem (oralt) A B C D M O AVSD är en romb, O är skärningspunkten för dess diagonaler, M är en punkt i rymden som inte ligger i rombens plan. Punkterna A, D, O ligger i planet α. Bestäm och motivera: 1. Vilka andra punkter ligger i planet α? Ligger punkterna B och M i planet α? Ligger punkt B i MOD:s plan? Namnge skärningslinjen för planen MOC och ADO. Punkt O är den gemensamma punkten för MOV- och MOC-planen. Är det sant att dessa plan skär varandra i en rät linje MO? Nämn tre raka linjer som ligger i samma plan; inte ligger i samma plan.

Problem (oralt) A B CM Sidorna AB och AC på triangeln ABC ligger i planet. Bevisa att medianen också ligger i planet.

S D V E F O M Uppgift (muntlig) Vilket är felet på ritningen, där O E F. Ge en förklaring. Hur en korrekt ritning ska se ut.

1 nivå A B C S K M N 1. Använd denna figur och nämn: a) fyra punkter som ligger i planet S AB; b) det plan i vilket den räta linjen MN ligger; c) en rät linje längs vilken planen S AC och S BC skär varandra. 2. Punkt C är den gemensamma punkten för planet och. Linje c går genom punkt C. Är det sant att planen och skär längs linjen c. Förklara svaret. 3. Genom linje a och punkt A kan två olika plan ritas. Vilken är den relativa positionen för linje a och punkt A. Förklara svaret. 2 nivå S А В С Д Е F 1. Använd denna figur, nämn: a) två plan som innehåller den räta linjen DE; b) den räta linje längs vilken planen AE F och S BC skär; c) plan som skärs av linjen S B. 2. Linjerna a, b och c har en gemensam punkt. Är det sant att dessa linjer ligger i samma plan? Motivera svaret. 3. Plan och skär i en rät linje med. Linje a ligger i planet och skär planet. Vilken är den relativa positionen för räta linjer a och c?

A B C D A 1 B 1 C 1 D 1 Nivå 3 (på kort) 1. Använd denna figur och nämn: a) två plan som innehåller linje B 1 C; b) en rät linje längs vilken planen В 1 СД och АА 1 Д 1 skär varandra; c) ett plan som inte skär den räta linjen SD 1. 2. Fyra raka linjer skär varandra i par. Är det sant att om tre av dem ligger i samma plan, så ligger alla fyra linjerna i samma plan? Förklara svaret. 3. Hörnet C på planetfyrhörningen AVSD ligger i planet, och punkterna A, B, D ligger inte i detta plan. Raka linjer AB och HELVETE skär planet vid punkterna B 1 respektive D 1. Vilken är den relativa positionen för punkterna C, B 1 och D 1? Förklara svaret.

Läxa: upprepa materialet från planimetri och gör anteckningar i anteckningsböcker om följande frågor: Bestämning av parallella linjer Inbördes position av två linjer på ett plan Konstruktion av en linje parallell med ett givet axiom för parallella linjer

1:a lektionen: Vad studerar stereometri? Stereometri är en gren av geometrin som studerar egenskaperna hos figurer i rymden. Ordet "stereometry" kommer från de grekiska orden "stereos" - volymetrisk, rumslig och "metero" - för att mäta. Många geometriska termer har översatts från det antika grekiska språket, eftersom geometri har sitt ursprung i det antika Grekland och utvecklats i filosofiska skolor.

2:a lektionen: Grundläggande former för stereometri. Det finns olika sätt att avbilda ett plan: planet avbildas med ett parallellogram; ett plan indikeras av en figur som begränsas av två parallella räta linjer och två godtyckliga kurvor; planet överförs av en figur av valfri form.

3:e lektionen: Rumsliga figurer. Lektionen ägnas åt förberedelser inför införandet av stereometrins axiom. Eleverna erbjuds följande uppgifter: 1. Rita en rät linje a, punkt A som ligger på den och punkt B som inte ligger på den 2. Rita ett plan och två skärande linjer a och b som ligger på den. 3. Rita planet, punkterna A och B som ligger på det, samt punkterna C och D på motsatta sidor av planet. 4. Rita planet och linjen som skär det. 5. Rita plan som skär varandra i räta vinklar.

5:e lektionen: Tecken på planparallellism. När vi studerar stereometrins axiom, minns vi de första axiomen för planimetri och formulerar deras rumsliga analogier. Som ett resultat får vi följande tabell: Ax uom a Ritningsformulering P1P1 Oavsett linje i rymden finns det punkter i rymden som hör till denna räta linje och punkter som inte tillhör den. P2P2 Genom två valfria punkter i rymden kan du rita en rak linje, och dessutom bara en.

6:e lektionen: Parallelldesign. Tänk på konsekvenserna av axiomen: Rita formulering Sl.1 Genom en rak linje och en punkt som inte ligger på den kan du rita ett plan, och dessutom bara ett. Om två punkter på en rät linje tillhör ett plan, så tillhör hela den räta linjen detta plan. Genom tre punkter som inte ligger på en rak linje kan du rita ett plan, och dessutom bara en.

Skildring av rumsliga figurer på ett plan Det finns sju lektioner om ämnet: 1. Parallell design och dess huvudsakliga egenskaper; 2. P Parallell utformning av plana figurer; 3. Och bilden av rumsliga figurer i parallell projektion; 4. C Sektion av polyedrar; 5. З Gyllene snittet; 6. Central design och dess egenskaper; 7. Och bilden av rumsliga figurer i den centrala projektionen.

Lektion 1: Parallelldesign och dess grundläggande egenskaper. Huvudegenskaperna för parallell design: 1. En parallell projektion av en rät linje är en rät linje eller en punkt; 2. en parallell projektion av ett linjesegment är ett linjesegment eller en punkt; 3. förhållandet mellan längderna av segmenten som ligger på en rät linje bevaras (i synnerhet mittpunkten av segmentet med parallell projektion går till mittpunkten av motsvarande segment); 4. Parallell projektion av två parallella linjer är parallella linjer, eller en linje, eller två punkter; 5. förhållandet mellan längderna av segmenten som ligger på parallella linjer bevaras under parallell design; 6. Om figuren ligger i ett plan parallellt med projektionsplanet, kommer dess parallella projektion på detta plan att vara en figur lika med den ursprungliga.

Lektion 2: Parallella projektioner av plana figurer. Frågan om bilden av platta figurer i parallell design övervägs. Eleverna ska föreställa sig vilka former som är parallella projektioner av polygoner och en cirkel. Ta reda på vilka egenskaper hos polygoner som bevaras under parallell design. Lär dig hur parallella projektioner av grundläggande plana figurer är konstruerade.

Det gyllene snittet i arkitekturen De berömda ryska arkitekterna M. Kazakov och V. Bazhenov använde i stor utsträckning det gyllene snittet i sitt arbete. Till exempel kan det gyllene snittet hittas i arkitekturen i senatsbyggnaden i Kreml. Enligt M. Kazakovs projekt byggdes den första kliniken i Moskva. Ett annat arkitektoniskt mästerverk i Moskva - Pashkovhuset - är en av de mest perfekta arkitekturdelarna av V. Bazhenov.

Polyedra. Denna kurs innehåller följande aktiviteter: 1. Regelbundna polyedrar. Vanliga polyedrar. 2. Halvregelbundna polyedrar. Halvregelbundna polyedrar. 3. Stjärnpolyedrar. Stjärnpolyeder. 4. Eulers sats. Eulers teorem.

Lektion 4: Eulers sats. En av de mest intressanta egenskaperna hos konvexa polyedrar beskrivs av Eulers teorem. Namn på polyeder a Antal hörn (B) Antal kant p (P) Antal ytor (D) Triangulär pyramid 464 Fyrkantig prisma 8126 Pentagonal bipyramid regelbunden dodekaeder n-vinkel pyramid n + 12n2n n-vinkel prisma 2n2n3n3nn + betrakta polyedrarna som de känner till och fyll i tabellen. Sedan härleds själva satsen: В-Р + Г = 2

Vinklar mellan linjer och plan i rymden. När man studerar detta ämne är det önskvärt att notera att problemet med att mäta vinklar går tillbaka till antiken. Historien om skapandet av mätinstrument och mätmetoder bör täckas så brett som möjligt. För detta föreslås det att genomföra följande klasser: 1. Volymen av figurer i rymden. Cylindervolym; Volymen av figurer i rymden. Cylindervolym; 2. Cavalieri-principen, Cavalieri-principen; 3. Konens volym; Konvolym; 4. Sfärens volym. Bollens volym.

Lektion 1: Volymen av figurer i rymden. Cylindervolym. Den här lektionen diskuterar problemen med att mäta volymen av rumsliga figurer. Volymens huvudsakliga egenskaper är uppräknade: oooooooooooooobrazovaniya figur i rymden är ett icke-negativt tal; oooo volymen av en kub med kant 1 är 1; muntliga figurer har lika stora volymer; oeo om figur Ф är sammansatt av figurerna Ф 1 och Ф 2, är volymen av figur Ф lika med summan av volymerna av figurerna Ф 1 och Ф 2.

Vad är stereometri?
Uppkomsten och utvecklingen av stereometri
Grundfigurer i rymden
Beteckning av punkter och exempel på deras modeller
Linjebeteckning
Exempel på modeller av raka linjer
Beteckning av plan och exempel på deras modeller
Vad mer studerar stereometri?
Objekt och geometriska kroppar runt omkring oss
Visar geometriska kroppar i ritningar
Det praktiska (tillämpade) värdet av stereometri
Stereometri axiom
Konsekvenser från stereometrins axiom
Förankring
Begagnade böcker

Vad är stereometri?

Stereometri Är ett avsnitt av geometrin där egenskaperna hos figurer i rymden studeras.

Uppkomsten och utvecklingen av stereometri.

Utvecklingen av stereometri började mycket senare än planimetri.
Stereometri utvecklades från observationer och lösningar på frågor som uppstod under mänsklig praktisk aktivitet.

Redan den primitiva människan, efter att ha tagit upp jordbruket, gjorde försök att åtminstone i grova termer uppskatta storleken på den skörd hon skördat av spannmålsmassorna som hopats i högar, högar eller staplar.
Byggaren av även de äldsta primitiva byggnaderna var tvungen att på något sätt ta hänsyn till det material som han hade till sitt förfogande, och även kunna beräkna hur mycket material som skulle krävas för att uppföra en viss byggnad.

Murverk bland de gamla egyptierna och kaldéerna krävde förtrogenhet med de metriska egenskaperna hos åtminstone de enklaste geometriska kropparna.
Behovet av jordbruk, navigering, orientering i tiden drev människor till astronomiska observationer, och de senare att studera egenskaperna hos sfären och dess delar, och följaktligen lagarna för det ömsesidiga arrangemanget av plan och linjer i rymden.

Grundfigurer i rymden.

Plan - en geometrisk figur som sträcker sig oändligt i alla riktningar

Beteckning av punkter och exempel på deras modeller.

Poäng betecknas med stora latinska bokstäver A, B, C, ...

Exempel på punktmodeller är:

atomer och molekyler

planeter i universums skala

Beteckning av raka linjer.

Raka linjer är betecknade:
latinska små bokstäver a, b, c, d, e, k, ...
två latinska versaler AB, CD ...

Exempel på modeller av linjer.

Exempel på linjemodeller är:

flygplanskontrailer

Beteckning av plan och exempel på deras modeller.

Planen betecknas med de grekiska bokstäverna α, β, γ, ...

Exempel på planmodeller är:

vattenyta

bordsyta

Vad mer studerar stereometri?

Tillsammans med en punkt, en linje och ett plan studerar stereometri geometriska kroppar och deras ytor.

Objekt och geometriska kroppar runt omkring oss.

Föremålen runt omkring oss ger idéer om geometriska kroppar.

Och genom att studera egenskaperna hos geometriska figurer – imaginära föremål, får vi information om de geometriska egenskaperna hos verkliga föremål och kan använda dessa egenskaper i praktiken.

kristaller-polyeder

plåtburk - cylinder

godisförpackning - kon

Bilder av geometriska kroppar i ritningar.

Bilden av en rumslig figur är dess projektion på ett visst plan.
Osynliga delar av figuren är ritade med streckade linjer.

Det praktiska (tillämpade) värdet av stereometri.

Geometriska kroppar är fiktiva föremål
Genom att studera egenskaperna hos geometriska former får vi idéer om de geometriska egenskaperna hos verkliga föremål (deras form, relativa position, etc.)
Stereometri används ofta inom konstruktion, arkitektur, maskinteknik och andra områden inom vetenskap och teknik.

Stereometri axiom.

Axiom- detta uttalande om egenskaperna hos geometriska figurer tas som utgångspunkt, utifrån vilka satser bevisas ytterligare och i allmänhet är all geometri konstruerad.

Stereometri axiom.

A1 . Genom tre valfria punkter som inte ligger på en rak linje passerar ett plan och dessutom bara en.

Stereometri axiom.

A2 ... Om två punkter på en rät linje ligger i ett plan, så ligger alla punkter på denna räta linje i detta plan.

I det här fallet säger de att en rak linje ligger i ett plan eller att ett plan passerar genom en rak linje.

Stereometri axiom.

A3. Om två plan har en gemensam punkt, så har de en gemensam rät linje på vilken alla de gemensamma punkterna för dessa plan ligger.

De säger att plan skär varandra i en rak linje

Konsekvenser från axiomen.

Sats 1: Ett plan passerar genom en rät linje och en punkt som inte ligger på den, och dessutom bara en.

Sats 2: Ett plan passerar genom två skärande linjer, och dessutom bara en.

Förankring.

1. Namnge planen där linjerna ligger:

Förankring.

2. Namnge skärningspunkten för linjen CE med planet ADB.

3. Namnge linjerna längs vilka planen skär:

Begagnade böcker

Geometri. 10-11 årskurser: lärobok. För allmänbildning. institutioner: grundläggande och profil. nivåer / HP Atanasyan, V.F. Butuzov, S.B. Kadomtsev et al. - 21:a uppl. - M .: Utbildning, 2012.- 255 s .: ill.
Geometri: Metodguide för högre pedagogiska institutioner och gymnasielärare: Del 2 Stereometri / utg. Prof. I.K. Andronov.

Skolgeometrikursen består av två delar:

PLANIMETRI
STEREOMETRI
Planimetri är en sektion
geometri där
egenskaper studeras
geometriska former
på ytan.
Stereometri är ett avsnitt
geometri där
egenskaper studeras
geometriska former
i rymden.
Ordet "stereometri" kommer från grekiskan
orden "stereos" - tredimensionell, rumslig och
"Metreo" - att mäta.
2

Grundläggande koncept

planimetri
Punkt
Hetero
stereometri
Punkt
Hetero
Plan
är en geometrisk figur,
sträcker sig på obestämd tid till alla
sidor.
3

Tillsammans med punkter, räta linjer, plan i stereometri, beaktas geometriska kroppar, deras egenskaper studeras, deras områden beräknas.

Tillsammans med punkter, linjer, plan
i stereometri
geometriska kroppar beaktas,
deras egenskaper studeras,
ytorna på deras ytor beräknas,
och även volymerna av kroppar beräknas.
kub
boll
cylinder
4

Volumetriska geometriska kroppar

Polyedra
Roterande kroppar
prisma
pyramid
kon
parallellepiped
cylinder
kub
boll
5

Poäng betecknas med stora latinska bokstäver A, B, C, D, E, K, ...

A
V
MED
E
Raka linjer indikeras med gemener
latinska bokstäverna a, b, c, d, e, k, ...
b
d
a
Plan är utsedda av grekiska
bokstäverna α, β, γ, λ, π, ω, ...
β
γ
α
6

Stereometri används ofta inom byggbranschen

Stereometri används inom arkitektur

Stereometri används inom maskinteknik

Stereometri används vid mätning

Geodesi är vetenskapen som studerar arten och
jordens storlek.
Inom många andra områden inom vetenskap och teknik.
10

Det är tydligt att i varje plan ligger några punkter i rymden, men inte alla punkter i rymden ligger i samma plan.

Aє, Bє,
M
Mє, Nє, Pє
A
N
B
P
11

Stereometri axiom

Axiom 1
Vilka tre som helst
poäng inte
ligger på en
rakt, passningar
plan, och
dessutom bara
ett.
A
V
MED
Axiom 3
Axiom 2
Om två
flygplan har
gemensam sak alltså
de har
rakt på
som alla ljuger
gemensamma punkter för dessa
flygplan.
Om två poäng
rakt ligga i
flygplan, då allt
punkter på en rät linje
ligga i detta
plan.
A
V
MED
A
a
α
12

Några konsekvenser av axiomen

F
α
a
P
M
Sats 2. Efter två
korsande räta linjer
passerar planet, och
dessutom bara en.
Sats 1. Över linjen
och inte ligga på den
punkten passerar planet,
och dessutom bara en.
b
a
α
M