Multiplication and division of negative numbers. Fraction. Multiplication and division of fractions

) And the denominator on the denominator (we get a denominator of the work).

Formula multiplication fractions:

For example:

Before proceeding with multiplication of numerators and denominators, you need to check reduced fractions . If it turns out to shorten the fraction, then you will be easier to carry out calculations.

Division of ordinary fraction on the fraction.

Division fractions with the participation of a natural number.

It's not as scary as it seems. As in the case of addition , We translate an integer into a fraction with a unit in the denominator. For example:

Multiplying mixed fractions.

Rules of multiplication of fractions (mixed):

• we transform mixed fractions into the wrong;
• reduce the numerals and denominators of fractions;
• reducing the fraction;
• if you got the wrong fraction, we transform the wrong fraction into a mixed one.

Note! To multiply mixed fraction On another mixed fraction, you need to begin, lead them to the mind of the wrong fractions, and then multiply by the rule of multiplication ordinary fractions.

The second method of multiplication of the fraction on a natural number.

It is more convenient to use the second way of multiplying an ordinary fraction for a number.

Note! For multiplication of fractions on natural number A denominator is needed to divide the number, and the numerator is left unchanged.

From the above, the example is clear that this option is more convenient for use when the denoter of the fraction is divided without a residue on a natural number.

Multi-storey fractions.

In high school classes, three-story (or more) fractions are found. Example:

To bring such a fraction to the usual mind, use division after 2 points:

Note!In dividing fractions, the order of division is very important. Be careful, it's easy to get confused here.

Note, eg:

When dividing units on any fraction, the result will the same fraction, only inverted:

Practical tips when multiplying and dividing fractions:

1. The most important in working with fractional expressions is accuracy and attentiveness. All calculations do carefully and gently, concentrately and clearly. Better write down a few unnecessary lines in the drafts, than getting confused in the calculations in the mind.

2. In tasks with different species fractions - go to the form of ordinary fractions.

3. All fractions reducing until it is impossible to cut.

4. Multi-storey fractional expressions We are looking into the form of ordinary, using the division after 2 points.

5. Unit of fraction divide in mind, just turning the fraction.

Now let's figure it out with multiplication and division.

Suppose we need to multiply +3 to -4. How to do it?

Let's consider such a case. Three people climbed into debt, and every 4 dollar debt. What is the total debt? In order to find it, it is necessary to fold all three debt: 4 dollars + 4 dollars + 4 dollars \u003d 12 dollars. We decided that the addition of three numbers 4 is indicated as 3 × 4. Since in this case we are talking about the debt, before 4 there is a sign "-". We know that the total debt is equal to 12 dollars, so now our task has the form 3x (-4) \u003d - 12.

We will get the same result if, by the condition of the task, each of the four people has a debt of 3 dollars. In other words, (+4) x (-3) \u003d - 12. And since the order of the factors does not matter, we obtain (-4) x (+3) \u003d - 12 and (+4) x (-3) \u003d - 12.

Let's summarize the results. With multiplying one positive and one negative number, the result will always be a negative number. The numerical amount of the answer will be the same as in the case of positive numbers. Work (+4) x (+3) \u003d + 12. The presence of a sign "-" affects only a sign, but does not affect the numerical value.

And how to multiply two negative numbers?

Unfortunately, this topic is very difficult to come up with a suitable example from life. It is easy to imagine a debt in the amount of 3 or 4 dollars, but it is absolutely impossible to imagine -4 or -3 people who climbed into debt.

Perhaps we will go different ways. In multiplication, when a sign of one of the multipliers changes the sign of the work. If we change signs from both multipliers, we must change twice sign of workFirst, with a positive on a negative, and then on the contrary, with a negative on a positive, that is, the work will have an initial sign.

Consequently, it is quite logical, although it is slightly strange that (-3) x (-4) \u003d + 12.

Sign position When multiply changed in this way:

• positive number x positive number \u003d positive number;
• negative number x positive number \u003d negative number;
• positive number x Negative number \u003d negative number;
• negative number x negative number \u003d positive number.

In other words, multipliering two numbers with the same signs, we get a positive number. Multiplying two numbers with different signswe get a negative number.

The same rule is valid for the opposite multiplication - for.

You can easily make sure by spending inverse operations multiplication. If in each of the examples given above, you multiply the private per divider, then get divisible, and make sure it has the same sign, for example (-3) x (-4) \u003d (+ 12).

Because winter is soon, then it's time to think about what to rebuild your iron horse, whatever it is to slide on ice and feel confident in winter roads. You can, for example, take the bus of Yokohama on the site: mvo.ru or some others, most importantly, whatever, more information And you can find prices on the site Mvo.ru.

In this lesson, multiplication and division is considered. rational numbers.

Design of lesson

Multiplying rational numbers

The rules for multiplying integers are valid for rational numbers. In other words, to multiply rational numbers, you need to be able to

Also, it is necessary to know the basic laws of multiplication, such as: Movement of multiplication, the combination law of multiplication, the distribution law of multiplication and multiplication by zero.

Example 1. Find an expression value

This is a multiplication of rational numbers with different signs. To multiply rational numbers with different signs, you need to multiply their modules and to put minus before the response received.

To see well to see what we are dealing with numbers who have different signs, enter each rational number in brackets together with your signs

The module of the number is equal, and the module of the number is equal. Moved the resulting modules as positive fractions, we got the answer, but before the answer was minus, as the rule required us. To ensure this minus before responding, the multiplication of the modules was performed in brackets, before which was minus.

A short solution is as follows:

Example 2. Find an expression value

Example 3. Find an expression value

This is a multiplication of negative rational numbers. To multiply negative rational numbers, you need to multiply their modules and in front of the response received to put plus

Solution for this example You can burn shorter:

Example 4. Find an expression value

The solution for this example can be written shorter:

Example 5. Find an expression value

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

A short solution will look much easier:

Example 6. Find an expression value

Transfer a mixed number to the wrong fraction. The rest will rewrite as it is

Received multiplication of rational numbers with different signs. Move the modules of these numbers and be minus before the response received. Recording with modules can be skipped to not clutter expression

The solution for this example can be written shorter

Example 7. Find an expression value

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

At first, the wrong shot turned out in the answer, but we allocated the whole part in it. note that whole part It was highlighted from the fraction module. The resulting mixed number was enclosed in brackets, before minus. This is done in order for the rule requirement. And the rule required that there was a minus before the response received.

The solution for this example can be written shorter:

Example 8. Find an expression value

First, change the number to the remaining number 5. Recording with modules will miss not to clutch expression.

Answer: The value of the expression equals -2.

Example 9. Find the value of the expression:

Translate mixed numbers In the wrong fraction:

Received multiplication of negative rational numbers. Move the modules of these numbers and in front of the response received, we will put a plus. Recording with modules can be skipped to not clutter expression

Example 10. Find an expression value

The expression consists of several factors. According to the combination law of multiplication, if the expression consists of several factors, then the work will not depend on the procedure. This allows us to calculate this expression in any order.

We will not be inventing the bike, and we calculate this expression from left to right in the order of the factory. Write with modules miss not to clutter expression

Third action:

Fourth action:

Answer: The value of the expression is equal

Example 11. Find an expression value

Remember the law of multiplication on zero. This law states that the work is zero, if at least one of the factors is zero.

In our example, one of the factors is zero, so without losing time responding that the value of the expression is zero:

Example 12. Find an expression value

The product is zero, if at least one of the factors is zero.

In our example, one of the factors is zero, so not losing time responding that the value of the expression Equally zero:

Example 13. Find an expression value

You can use the procedure for actions and first calculate the expression in brackets and multiply the result with a fraction.

You can still take advantage of the distribution law of multiplication - multiply every term of the fraction and the results obtained. In this way, we use.

According to the Procedure, if addition and multiplication is present in the expression, then first need to perform multiplication. Therefore, in the resulting new expression, we take in brackets those parameters that should be multiplied. So we will see well what actions perform earlier, and what later:

Third action:

Answer: The value of the expression equally

The solution for this example can be recorded significantly shorter. It will look like this:

It can be seen that this example could be solved even in the mind. Therefore, the expression analysis skill should be developed before it began. It is likely that it can be solved in the mind and save a lot of time and nerves. And in the control and exams, as it is known to be very expensive.

Example 14. Find an expression value -4.2 × 3.2

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

Pay attention to how the modules of rational numbers multiplied. In this case, in order to multiply the modules of rational numbers, it was required.

Example 15. Find an expression value -0.15 × 4

This is a multiplication of rational numbers with different signs. Move the modules of these numbers and put minus before the response received

Pay attention to how the modules of rational numbers multiplied. In this case, in order to multiply the modules of rational numbers, it was necessary to be able.

Example 16. Find an expression value -4.2 × (-7.5)

This is a multiplication of negative rational numbers. Move the modules of these numbers and before the response received, we will put a plus

Division of rational numbers

The rules for dividing the integers are valid for rational numbers. In other words, to be able to share rational numbers, you need to be able to

The rest of the same methods of dividing ordinary and decimal fractions are used. To divide the ordinary fraction on another fraction, you need to multiply the first fraction to fraction, reverse second.

And to divide decimal fraction On another decimal fraction, you need to move the comma to the right to the right on so many numbers as they are after the comma in the divider, then make division as the usual number.

Example 1. Find the value of the expression:

This division of rational numbers with different signs. To calculate such an expression, you need to multiply the first fraction to the fraction, inverse second.

So, I will multiply the first fraction for the fraction inverse second.

Received multiplication of rational numbers with different signs. And how to calculate such expressions we already know. To do this, multiply the modules of these rational numbers and to put minus before the response received.

Take this example to the end. Recording with modules can be skipped to not clutter expression

Thus, the value of the expression is equal

A detailed solution is as follows:

A short solution will look like this:

Example 2. Find an expression value

This division of rational numbers with different signs. To calculate this expression, you need to multiply the first fraction to the fraction, inverse second.

The reverse for the second fraction is a fraction. For her and multiply the first fraction:

A short solution will look like this:

Example 3. Find an expression value

This division of negative rational numbers. To calculate this expression, again, you need to multiply the first fraction in the fraction inverse second.

The reverse for the second fraction is a fraction. For her and multiply the first fraction:

Received multiplication of negative rational numbers. As a calculated such expression, we already know. It is necessary to multiply the modules of rational numbers and before the response received is plus.

Dore this example to the end. Recording with modules can be skipped to not clutter expression:

Example 4. Find an expression value

To calculate this expression, you need the first number -3 to multiply by fraction, inverse fraction.

Reverse for a fraction this fraction. On her and multiply the first number -3

Example 6. Find an expression value

To calculate this expression, you need to multiply the first fraction by the number, reverse number 4.

The reverse for the number 4 is a fraction. On it and multiply the first fraction

Example 5. Find an expression value

To calculate this expression, you need to multiply the first fraction to the number, the reverse number -3

Inverse for a number -3 is a fraction. For her and multiply the first fraction:

Example 6. Find an expression -14,4: 1.8

This division of rational numbers with different signs. To calculate this expression, you need to divide the divide module to the divisor module and put a minus before the response received

Note how the divisory module was divided into the divider module. In this case, to make it right, it took to be able to be able.

If there is no desire to mess with decimal fractions (and it happens often), then these, then translate these mixed numbers into the wrong fraction, and then do the division directly.

We calculate the previous expression -14.4: 1.8 in this way. Transfer decimal fractions into mixed numbers:

Now we will transfer the resulting mixed numbers to the wrong fraction:

Now you can go directly to the division, namely split the fraction for the fraction. To do this, you need to multiply the first fraction, inverse the second:

Example 7. Find an expression value

We translate the decimal fraction -2.06 to the wrong fraction, and multiply this fraction for the fraction, inverse second:

Multi-storey fractions

Often you can find an expression in which the division of fractions is written using a fractional feature. For example, the expression can be recorded as follows:

What is the difference between expressions and? In fact, no difference. These two expressions carry the same meaning and between them can be put a sign of equality:

In the first case, the division sign is a colon and the expression is recorded in one line. In the second case, the division of fractions is written using a fractional feature. As a result, it turns out a fraction, which the people agreed to call multi-storey.

When meeting with such multi-storey expressions, you need to apply the same rules for dividing ordinary fractions. The first fraction must be multiplied by the fraction, inverse second.

Use in solving such fractions is extremely inconvenient, so you can write them in understandable, using a non-fractional line as a sign, and a colon.

For example, we write a multi-storey fraction in understandable. To do this, you first need to figure out where the first fraction and where the second, because it is not always possible to do it correctly. In multi-storey fractions there are several fractional traits that can be confused. The main fractional feature, which separates the first fraction from the second, is usually longer than the rest.

After determining the main fractional line, you can easily understand where the first fraction and where the second:

Example 2.

We find the main fractional line (it is the longest) and we see that the division of an integer -3 one is carried out on an ordinary fraction

And if we mistakenly accepted the second fractional feature for the main thing (the one is shorter), it would have been that we divide the fraction for an integer 5 in this case, even if this expression is to calculate correctly, the task will be solved incorrect because divisible in this The case is the number -3, and the divider - the fraction.

Example 3. We write in understandable form a multi-storey fraction

We find the main fractional line (it is the longest) and see that the fraction is carried out by an integer 2

And if we mistakenly accepted the first fractional feature for the main thing (the one is shorter), it would have done that we would divide the whole number -5 on the fraction in this case, even if this expression is true, the task will be solved incorrectly because divisible In this case, the fraction is, and the divider is an integer 2.

Despite the fact that multi-storey fractions are uncomfortable in work, we will face with them very often, especially when studying the highest mathematics.

Naturally, the translation of a multi-storey fraction in a clear species takes extra time and place. Therefore, you can use more fast method. This method is convenient and at the output allows you to get a ready-made expression in which the first fraction is already multiplied by fraction, inverse second.

This method is implemented as follows:

If the fraction is a four-storey, for example, like, the figure on the first floor is raised to the top floor. And the figure located on the second floor is raised by the third floor. The figures obtained need to connect the multiplication icons (×)

As a result, bypassing the intermediate record, we obtain a new expression in which the first fraction is already multiplied by the fraction, inverse second. Convenience and only!

To prevent errors when using this method, It can be guided by the following rule:

From the first to the fourth. From the second on the third.

In Rule we are talking about the floors. The number from the first floor should be raised on the fourth floor. And the number from the second floor you need to raise on the third floor.

Let's try to calculate the multi-storey fraction using the above rule.

So, the figure located on the first floor raise the fourth floor, and I raise the figure on the second floor to the third floor

As a result, bypassing the intermediate entry, we obtain a new expression in which the first fraction is already multiplied by the fraction, inverse second. Next, you can take advantage of the knowledge:

Let's try to calculate the multi-storey fraction using the new scheme.

There is only the first, second and fourth floors. The third floor is absent. But we do not move away from the main scheme: I raise the figure from the first floor to the fourth floor. And since there is no third floor, then leave the figure on the second floor, as is

As a result, bypassing the intermediate entry, we received a new expression, in which the first number -3 is already multiplied by the fraction, inverse second. Next, you can take advantage of the knowledge:

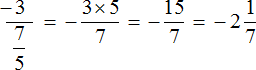
Let's try to calculate the multi-storey fraction using a new scheme.

There is only the second, third and fourth floors. The first floor is absent. Since there is no first floor, it is there for a fourth floor, but we can raise the number from the second floor to the third:

As a result, bypassing the intermediate entry, we received a new expression, in which the first fraction is already multiplied by the reverse divider. Next, you can take advantage of the knowledge:

Using variables

If the expression is complex and it seems to you that it will confuse you in the process of solving the problem, then part of the expression can be added to the variable and then work with this variable.

Mathematics often do. The challenging task is divided into more easy subtasks and solve them. Then they collect solved subtasks into one single integer. This is a creative process and it is studying for years, training hard.

The use of variables is justified when working with multi-storey fractions. For example:

Find an expression value

So, there is a fractional expression in the numerator and in the denominator which fractional expressions. In other words, we are again a multi-storey fraction that we do not like that.

The expression located in the numerator can be entered into a variable with any name, for example:

But in mathematics in this case, the variables take the name from large Latin letters. Let's not violate this tradition, and we denote the first expression through the Latin Latin letter A

And the expression located in the denominator can be denoted through a large Latin letter B

Now our initial expression takes appearance. That is, we made a replacement numerical expression On the letter, pre-enlightened the numerator and denominator in Variables A and B.

Now we can separately calculate the values \u200b\u200bof the variable A and the value of the variable B. The finished values \u200b\u200bwe insert into the expression.

Find the value of the variable A.

Find the value of the variable B.

Now we substitute in the main expression instead of variables a and b of their meanings:

We got a multi-storey fraction in which you can use the scheme "from the first to the fourth, from the second to the third", that is, the figure located on the first floor to raise on the fourth floor, and the figure is on the second floor to raise the third floor. Further computation will not be much difficulty:

Thus, the value of the expression is -1.

Of course, we considered the simplest exampleBut our goal was to know how to use variables to facilitate yourself tasks to minimize error assumptions.

We also note that the solution for this example can be recorded without applying variables. It will look like

This solution is faster and short and in this case it is more expedient to write it down, but if the expression is complex, consisting of several parameters, brackets, roots and degrees, it is advisable to calculate it in several steps, enters part of its expressions into variables.

Did you like the lesson?
Join our new group VKontakte and start receiving notifications about new lessons