چگونه یک عبارت را ساده کنیم 8. تبدیل عبارات. نظریه تفصیلی (2019). روش های ساده سازی اضافی
در ابتدای درس، ویژگیهای اساسی ریشههای مربع را مرور میکنیم و سپس به چند مثال پیچیده از سادهسازی عبارات حاوی جذر میپردازیم.
موضوع:تابع. خواص جذر
درس:تبدیل و ساده سازی عبارات پیچیده تر با ریشه
1. بررسی خواص ریشه مربع
اجازه دهید به طور خلاصه این تئوری را تکرار کنیم و ویژگی های اساسی ریشه های مربع را به یاد بیاوریم.
خواص ریشه های مربع:
1. بنابراین، ;
3. ![]() ;
;
4. ![]() .
.
2. مثال هایی برای ساده سازی عبارات با ریشه
بیایید به سراغ نمونه هایی از استفاده از این ویژگی ها برویم.
مثال 1: یک عبارت را ساده کنید ![]() .
.
راه حل. برای ساده تر، عدد 120 باید به فاکتورهای اول فاکتور شود:
مجذور حاصل را با استفاده از فرمول مناسب نشان می دهیم:
مثال 2: یک عبارت را ساده کنید ![]() .
.
راه حل. بیایید در نظر بگیریم که این عبارت برای همه مقادیر ممکن متغیر معنی ندارد، زیرا این عبارت حاوی ریشه های مربع و کسری است که منجر به "تعریف" دامنه مقادیر مجاز می شود. ODZ:  ().
().
بیایید عبارت داخل پرانتز را به مخرج مشترک بیاوریم و عدد کسر آخر را به عنوان تفاضل مربع بنویسیم:
پاسخ. در
مثال 3: یک عبارت را ساده کنید ![]() .
.
راه حل. مشاهده میشود که براکت شمارهگذار دوم ظاهر نامناسبی دارد و نیاز به سادهسازی دارد؛ بیایید سعی کنیم آن را با استفاده از روش گروهبندی فاکتور کنیم.
برای اینکه بتوانیم یک عامل مشترک را استخراج کنیم، ریشه ها را با فاکتورگیری آنها ساده کردیم. بیایید عبارت حاصل را با کسر اصلی جایگزین کنیم:
پس از کاهش کسر، فرمول اختلاف مربع ها را اعمال می کنیم.
3. مصداق رهایی از بی منطقی
مثال 4. خود را از بی منطقی (ریشه) در مخرج رها کنید: a) ; ب) .
راه حل. الف) برای رهایی از غیرمنطقی بودن در مخرج، از روش استاندارد ضرب هر دو صورت و مخرج کسری در ضریب مزدوج در مخرج استفاده می شود (همان عبارت، اما با علامت مخالف). این کار برای تکمیل مخرج کسری به اختلاف مربع ها انجام می شود که به شما امکان می دهد از ریشه های مخرج خلاص شوید. بیایید این کار را در مورد خود انجام دهیم:
ب) انجام اقدامات مشابه:
4. مثال برای اثبات و شناسایی یک مربع کامل در یک رادیکال پیچیده
مثال 5. برابری را ثابت کنید ![]() .
.
اثبات بیایید از تعریف یک جذر استفاده کنیم که از آن نتیجه می شود که مربع عبارت سمت راست باید با عبارت رادیکال برابر باشد:
![]() . بیایید پرانتزها را با استفاده از فرمول مجذور مجموع باز کنیم:
. بیایید پرانتزها را با استفاده از فرمول مجذور مجموع باز کنیم:
![]() ، برابری صحیح را بدست آوردیم.
، برابری صحیح را بدست آوردیم.
اثبات شده است.
مثال 6. عبارت را ساده کنید.
راه حل. این عبارت معمولاً رادیکال پیچیده (ریشه زیر ریشه) نامیده می شود. در این مثال، شما باید بفهمید که چگونه یک مربع کامل را از عبارت رادیکال جدا کنید. برای انجام این کار، توجه داشته باشید که از بین دو عبارت، نامزدی برای نقش حاصلضرب مضاعف در فرمول اختلاف مجذور است (تفاوت، زیرا منهای وجود دارد). اجازه دهید آن را به شکل حاصلضرب زیر بنویسیم: ، سپس 1 ادعا می کند که یکی از عبارت های مربع کامل است و 1 ادعا می کند که دومی است.
بیایید این عبارت را زیر ریشه جایگزین کنیم.
ساده کردن عبارات جبری یکی از کلیدهای یادگیری جبر است و یک مهارت فوق العاده مفید برای همه ریاضیدانان است. ساده سازی به شما امکان می دهد یک عبارت پیچیده یا طولانی را به یک عبارت ساده که کار با آن آسان است کاهش دهید. مهارت های اولیه ساده سازی حتی برای کسانی که علاقه ای به ریاضیات ندارند خوب است. با پیروی از چند قانون ساده، می توانید بسیاری از رایج ترین انواع عبارات جبری را بدون دانش ریاضی خاص ساده کنید.
مراحل
تعاریف مهم
-
اعضای مشابه . اینها اعضایی هستند با متغیرهای یکسان، اعضایی با متغیرهای یکسان یا اعضای آزاد (اعضایی که دارای متغیر نیستند). به عبارت دیگر، اصطلاحات مشابه شامل یک متغیر به همان درجه، شامل چندین متغیر یکسان یا اصلاً شامل یک متغیر نیستند. ترتیب اصطلاحات در بیان مهم نیست.
- به عنوان مثال، 3x 2 و 4x 2 اصطلاحات مشابهی هستند زیرا حاوی یک متغیر مرتبه دوم (به توان دوم) "x" هستند. با این حال، x و x2 اصطلاحات مشابهی نیستند، زیرا حاوی متغیر "x" از مرتبه های مختلف (اول و دوم) هستند. به همین ترتیب، -3yx و 5xz اصطلاحات مشابهی نیستند زیرا دارای متغیرهای مختلفی هستند.
-
فاکتورسازی . این یافتن اعدادی است که حاصلضرب آنها به عدد اصلی منتهی می شود. هر عدد اصلی می تواند چندین عامل داشته باشد. به عنوان مثال، عدد 12 را می توان در مجموعه عوامل زیر فاکتور گرفت: 1 × 12، 2 × 6 و 3 × 4، بنابراین می توان گفت که اعداد 1، 2، 3، 4، 6 و 12 عواملی هستند. شماره 12. فاکتورها همان ضرایب هستند، یعنی اعدادی که عدد اصلی بر آنها تقسیم می شود.
- به عنوان مثال، اگر می خواهید عدد 20 را فاکتور کنید، آن را به این صورت بنویسید: 4×5.
- توجه داشته باشید که هنگام فاکتورگیری، متغیر در نظر گرفته می شود. به عنوان مثال، 20x = 4 (5x).
- اعداد اول را نمی توان فاکتور گرفت زیرا آنها فقط بر خود و 1 بخش پذیر هستند.
-
برای جلوگیری از اشتباه، ترتیب عملیات را به خاطر بسپارید و دنبال کنید.
- براکت ها
- درجه
- ضرب
- بخش
- اضافه شدن
- منها کردن
آوردن اعضای مشابه
-
عبارت را بنویسید.عبارات جبری ساده (آنهایی که شامل کسر، ریشه و غیره نیستند) تنها در چند مرحله قابل حل (ساده شدن) هستند.
- به عنوان مثال، عبارت را ساده کنید 1 + 2x - 3 + 4x.
-
اصطلاحات مشابه را تعریف کنید (اصطلاحاتی با متغیرهای یکسان، اصطلاحاتی با متغیرهای یکسان یا اصطلاحات آزاد).
- اصطلاحات مشابه را در این عبارت بیابید. اصطلاحات 2x و 4x حاوی متغیری با همان ترتیب (اول) هستند. همچنین 1 و -3 اصطلاحات آزاد هستند (متغیر ندارند). بنابراین، در این عبارت اصطلاحات 2 برابر و 4 برابرمشابه هستند و اعضا 1 و -3نیز مشابه هستند.
-
اعضای مشابه بدهید.این به معنای جمع یا تفریق آنها و ساده کردن عبارت است.
- 2x + 4x = 6 برابر
- 1 - 3 = -2
-
عبارت را با در نظر گرفتن عبارات داده شده بازنویسی کنید.یک عبارت ساده با اصطلاحات کمتر دریافت خواهید کرد. عبارت جدید برابر با عبارت اصلی است.
- در مثال ما: 1 + 2x - 3 + 4x = 6x - 2، یعنی عبارت اصلی ساده شده و کار با آن راحت تر است.
-
هنگام آوردن اعضای مشابه ترتیب عملیات را رعایت کنید.در مثال ما، ارائه شرایط مشابه آسان بود. اما در مورد عبارات پیچیده ای که اصطلاحات در داخل پرانتز قرار می گیرند و کسرها و ریشه ها وجود دارد، آوردن چنین اصطلاحاتی چندان آسان نیست. در این موارد، ترتیب عملیات را دنبال کنید.
- به عنوان مثال، عبارت 5(3x - 1) + x((2x)/(2)) + 8 - 3x را در نظر بگیرید. در اینجا اشتباه است که فوراً 3x و 2x را به عنوان اصطلاحات مشابه تعریف کرده و آنها را ارائه کنیم، زیرا ابتدا باید پرانتزها را باز کنیم. بنابراین عملیات را طبق ترتیب آنها انجام دهید.
- 5 (3x-1) + x((2x)/(2)) + 8 - 3x
- 15x - 5 + x(x) + 8 - 3x
- 15x - 5 + x 2 + 8 - 3x. اکنون، هنگامی که عبارت فقط شامل عملیات جمع و تفریق می شود، می توانید عبارات مشابه را بیاورید.
- x 2 + (15x - 3x) + (8 - 5)
- x 2 + 12x + 3
- به عنوان مثال، عبارت 5(3x - 1) + x((2x)/(2)) + 8 - 3x را در نظر بگیرید. در اینجا اشتباه است که فوراً 3x و 2x را به عنوان اصطلاحات مشابه تعریف کرده و آنها را ارائه کنیم، زیرا ابتدا باید پرانتزها را باز کنیم. بنابراین عملیات را طبق ترتیب آنها انجام دهید.
ضریب را از پرانتز خارج کنید
-
پیدا کردن بزرگترین مقسوم علیه مشترک(GCD) تمام ضرایب عبارت. GCD بزرگترین عددی است که تمام ضرایب عبارت بر آن تقسیم می شود.
- به عنوان مثال، معادله 9x 2 + 27x - 3 را در نظر بگیرید. در این حالت، GCD = 3، زیرا هر ضریب این عبارت بر 3 بخش پذیر است.
-
هر عبارت عبارت را بر gcd تقسیم کنید.عبارات حاصل ضرایب کوچکتری نسبت به عبارت اصلی دارند.
- در مثال ما، هر عبارت عبارت را بر 3 تقسیم کنید.
- 9x 2/3 = 3x 2
- 27x/3 = 9x
- -3/3 = -1
- نتیجه یک بیان بود 3x 2 + 9x - 1. با عبارت اصلی برابری نمی کند.
- در مثال ما، هر عبارت عبارت را بر 3 تقسیم کنید.
-
عبارت اصلی را برابر حاصل ضرب gcd و عبارت حاصل بنویسید.یعنی عبارت حاصل را در براکت قرار دهید و gcd را از داخل براکت خارج کنید.
- در مثال ما: 9x 2 + 27x - 3 = 3 (3x 2 + 9x - 1)
-
ساده کردن عبارات کسری با قرار دادن فاکتور خارج از پرانتز.چرا به سادگی ضریب را خارج از پرانتز قرار دهید، همانطور که قبلا انجام شد؟ سپس، برای یادگیری نحوه ساده سازی عبارات پیچیده، مانند عبارات کسری. در این حالت، قرار دادن ضریب خارج از پرانتز می تواند به خلاص شدن از شر کسر (از مخرج) کمک کند.
- به عنوان مثال، عبارت کسری (9x 2 + 27x - 3)/3 را در نظر بگیرید. برای ساده کردن این عبارت از فاکتور برداری استفاده کنید.
- ضریب 3 را خارج از پرانتز قرار دهید (همانطور که قبلاً انجام دادید): (3(3x 2 + 9x - 1))/3
- توجه داشته باشید که هم اکنون یک عدد 3 در صورت و مخرج وجود دارد.
- از آنجایی که هر کسری که عدد 1 را در مخرج داشته باشد به سادگی با صورت برابر است، عبارت کسری اصلی به صورت زیر ساده می شود: 3x 2 + 9x - 1.
- به عنوان مثال، عبارت کسری (9x 2 + 27x - 3)/3 را در نظر بگیرید. برای ساده کردن این عبارت از فاکتور برداری استفاده کنید.
روش های ساده سازی اضافی
-
ساده سازی عبارات کسریهمانطور که در بالا ذکر شد، اگر صورت و مخرج هر دو دارای اصطلاحات یکسان (یا حتی عبارات یکسان) باشند، می توان آنها را کاهش داد. برای این کار باید فاکتور مشترک صورت یا مخرج یا هر دو صورت و مخرج را از داخل پرانتز خارج کنید. یا می توانید هر جمله در صورت را بر مخرج تقسیم کنید و در نتیجه عبارت را ساده کنید.
- به عنوان مثال، عبارت کسری (5x 2 + 10x + 20)/10 را در نظر بگیرید. در اینجا، به سادگی هر عبارت عددی را بر مخرج (10) تقسیم کنید. اما توجه داشته باشید که عبارت 5x2 به طور مساوی بر 10 بخش پذیر نیست (زیرا 5 کمتر از 10 است).
- بنابراین یک عبارت ساده شده مانند این بنویسید: ((5x 2)/10) + x + 2 = (1/2)x 2 + x + 2.
- به عنوان مثال، عبارت کسری (5x 2 + 10x + 20)/10 را در نظر بگیرید. در اینجا، به سادگی هر عبارت عددی را بر مخرج (10) تقسیم کنید. اما توجه داشته باشید که عبارت 5x2 به طور مساوی بر 10 بخش پذیر نیست (زیرا 5 کمتر از 10 است).
-
ساده سازی عبارات رادیکال.به عبارات زیر علامت ریشه اصطلاحات رادیکال می گویند. آنها را می توان از طریق تجزیه آنها به عوامل مناسب و حذف بعدی یک عامل از زیر ریشه ساده کرد.
- بیایید به یک مثال ساده نگاه کنیم: √(90). عدد 90 را می توان در فاکتورهای زیر فاکتور کرد: 9 و 10 و از 9 می توان جذر (3) را گرفت و 3 را از زیر ریشه خارج کرد.
- √(90)
- √ (9×10)
- √(9)×√(10)
- 3×√(10)
- 3√(10)
- بیایید به یک مثال ساده نگاه کنیم: √(90). عدد 90 را می توان در فاکتورهای زیر فاکتور کرد: 9 و 10 و از 9 می توان جذر (3) را گرفت و 3 را از زیر ریشه خارج کرد.
-
ساده سازی عبارات با قدرت.برخی از عبارات شامل عملیات ضرب یا تقسیم عبارت با توان هستند. در صورت ضرب عبارات با پایه یکسان، توان آنها اضافه می شود. در صورت تقسیم عبارت با پایه یکسان، توان آنها کم می شود.
- به عنوان مثال، عبارت 6x 3 × 8x 4 + (x 17 /x 15) را در نظر بگیرید. در صورت ضرب، توان ها را جمع کنید و در صورت تقسیم، آنها را کم کنید.
- 6 x 3 × 8 x 4 + (x 17 / x 15)
- (6 × 8) x 3 + 4 + (x 17 - 15)
- 48 x 7 + x 2
- در ادامه قوانین ضرب و تقسیم عبارت با توان ها را توضیح می دهیم.
- ضرب عبارت با توان برابر است با ضرب عبارت در خود. به عنوان مثال، از آنجایی که x 3 = x × x × x و x 5 = x × x × x × x × x، پس x 3 × x 5 = (x × x × x) × (x × x × x × x × x)، یا x 8.
- به همین ترتیب، تقسیم عبارتها با درجهها معادل تقسیم عبارتها بر خودشان است. x 5 / x 3 = (x × x × x × x × x) / (x × x × x). از آنجایی که عبارات مشابه موجود در صورت و مخرج را می توان کاهش داد، حاصل ضرب دو "x" یا x 2 در صورتگر باقی می ماند.
- به عنوان مثال، عبارت 6x 3 × 8x 4 + (x 17 /x 15) را در نظر بگیرید. در صورت ضرب، توان ها را جمع کنید و در صورت تقسیم، آنها را کم کنید.
عبارات و کسرهای گویا سنگ بنای کل درس جبر هستند. کسانی که یاد می گیرند با چنین عباراتی کار کنند، آنها را ساده کرده و آنها را فاکتورسازی کنند، اساساً قادر به حل هر مشکلی خواهند بود، زیرا تبدیل عبارات بخشی جدایی ناپذیر از هر معادله جدی، نابرابری یا حتی مشکل کلمه است.
در این آموزش ویدیویی نحوه استفاده صحیح از فرمول های ضرب اختصاری برای ساده سازی عبارات و کسرهای منطقی را بررسی خواهیم کرد. بیایید یاد بگیریم که این فرمول ها را در جایی که در نگاه اول چیزی وجود ندارد ببینیم. در همان زمان، ما یک تکنیک ساده مانند فاکتورگیری یک مثلث درجه دوم از طریق یک ممیز را تکرار خواهیم کرد.
همانطور که احتمالاً قبلاً از فرمول های پشت سر من حدس زده اید، امروز ما فرمول های ضرب اختصاری یا، به طور دقیق تر، نه خود فرمول ها، بلکه استفاده از آنها را برای ساده سازی و کاهش عبارات پیچیده منطقی مطالعه خواهیم کرد. اما، قبل از رفتن به حل مثالها، اجازه دهید نگاهی دقیقتر به این فرمولها بیندازیم یا آنها را به خاطر بسپاریم:
- $((a)^(2))-((b)^(2))=\left(a-b \right)\left(a+b \right)$ - تفاوت مربع ها.
- $((\left(a+b \right))^(2))=((a)^(2))+2ab+((b)^(2))$ مربع مجموع است.
- $((\left(a-b \راست))^(2))=((a)^(2))-2ab+((b)^(2))$ — مجذور اختلاف;
- $((a)^(3))+((b)^(3))=\left(a+b \right)\left(((a)^(2))-ab+((b)^( 2)) \right)$ مجموع مکعب ها است.
- $((a)^(3))-((b)^(3))=\left(a-b \right)\left(((a)^(2))+ab+((b)^(2) ) \right)$ تفاوت مکعب ها است.
همچنین می خواهم توجه داشته باشم که سیستم آموزشی مدرسه ما به گونه ای ساختار یافته است که با مطالعه این موضوع، یعنی. عبارات منطقی، و همچنین ریشه ها، ماژول ها، همه دانش آموزان همین مشکل را دارند که اکنون توضیح خواهم داد.
واقعیت این است که در همان ابتدای مطالعه فرمول های ضرب اختصاری و بر این اساس، اقدامات برای کاهش کسری (این جایی در کلاس هشتم است)، معلمان چیزی شبیه به زیر می گویند: "اگر چیزی برای شما روشن نیست، پس انجام ندهید" نگران نباش، ما به شما کمک خواهیم کرد. بعداً این موضوع را بررسی خواهیم کرد." خوب، پس در نوبت کلاس های 9-10، همان معلمان به همان دانش آموزانی که هنوز نمی دانند چگونه کسرهای منطقی را حل کنند توضیح می دهند، چیزی شبیه به این: "دو سال قبل کجا بودید؟ این در جبر در کلاس هشتم مطالعه شد! چه چیزی می تواند در اینجا نامشخص باشد؟ خیلی واضح است!»
با این حال، چنین توضیحاتی کار را برای دانشآموزان عادی آسانتر نمیکند: آنها هنوز در سرشان آشفتگی داشتند، بنابراین در حال حاضر به دو مثال ساده نگاه میکنیم که بر اساس آنها خواهیم دید که چگونه این عبارات را در مسائل واقعی جدا کنیم. ، که ما را به فرمول های ضرب اختصاری و نحوه اعمال آن برای تبدیل عبارات پیچیده منطقی هدایت می کند.
کاهش کسرهای گویا ساده
وظیفه شماره 1
\[\frac(4x+3((y)^(2)))(9((y)^(4))-16((x)^(2)))\]
اولین چیزی که باید یاد بگیریم این است که مربع های دقیق و قدرت های بالاتر را در عبارات اصلی شناسایی کنیم، که بر اساس آن می توانیم فرمول ها را اعمال کنیم. بیایید نگاهی بیندازیم:
بیایید بیان خود را با در نظر گرفتن این حقایق بازنویسی کنیم:
\[\frac(4x+3((y)^(2)))((\چپ(3((y)^(2)) \راست))^(2))-((\چپ(4x \راست))^(2))=\frac(4x+3((y)^(2)))(\left(3((y)^(2))-4x \راست)\چپ(3 ((y)^(2))+4x \راست))=\frac(1)(3((y)^(2))-4x)\]
پاسخ: $\frac(1)(3((y)^(2))-4x)$.
مشکل شماره 2
بریم سراغ کار دوم:
\[\frac(8)(((x)^(2))+5xy-6((y)^(2)))\]
در اینجا چیزی برای ساده کردن وجود ندارد، زیرا شمارش حاوی یک ثابت است، اما من این مسئله را دقیقاً پیشنهاد کردم تا یاد بگیرید چگونه چند جمله ای های حاوی دو متغیر را فاکتور بگیرید. اگر به جای آن چند جمله ای زیر را داشته باشیم، چگونه آن را بسط می دهیم؟
\[((x)^(2))+5x-6=\چپ(x-... \راست)\چپ(x-... \راست)\]
بیایید معادله را حل کنیم و x$ را که میتوانیم به جای نقطهها قرار دهیم، پیدا کنیم:
\[((x)^(2))+5x-6=0\]
\[((x)_(1))=\frac(-5+7)(2)=\frac(2)(2)=1\]
\[((x)_(2))=\frac(-5-7)(2)=\frac(-12)(2)=-6\]
سه جمله ای را می توانیم به صورت زیر بازنویسی کنیم:
\[((x)^(2))+5xy-6((y)^(2))=\چپ(x-1 \راست)\چپ(x+6 \راست)\]
ما یاد گرفتیم که چگونه با یک مثلث درجه دوم کار کنیم - به همین دلیل لازم بود این درس ویدیویی را ضبط کنیم. اما اگر علاوه بر $x$ و یک ثابت، $y$ نیز وجود داشته باشد، چه؟ بیایید آنها را به عنوان یکی دیگر از عناصر ضرایب در نظر بگیریم، i.e. بیایید عبارت خود را به صورت زیر بازنویسی کنیم:
\[((x)^(2))+5y\cdot x-6((y)^(2))\]
\[((x)_(1))=\frac(-5y+7y)(2)=y\]
\[((x)_(2))=\frac(-5y-7y)(2)=\frac(-12y)(2)=-6y\]
اجازه دهید بسط ساخت مربع خود را بنویسیم:
\[\چپ(x-y \راست)\چپ(x+6y \راست)\]
بنابراین، اگر به عبارت اصلی برگردیم و با در نظر گرفتن تغییرات آن را بازنویسی کنیم، به شکل زیر میرسیم:
\[\frac(8)(\left(x-y \راست)\left(x+6y \راست))\]
چنین رکوردی چه چیزی به ما می دهد؟ هیچ، چون قابل کاهش نیست، در هیچ چیز ضرب و تقسیم نمی شود. با این حال، به محض اینکه معلوم شود این کسر جزء جدایی ناپذیر یک عبارت پیچیده تر است، چنین بسطی مفید خواهد بود. بنابراین، به محض مشاهده یک مثلث درجه دوم (مهم نیست که آیا بار پارامترهای اضافی است یا نه)، همیشه سعی کنید آن را فاکتور بگیرید.
تفاوت های ظریف راه حل
قوانین اساسی برای تبدیل عبارات منطقی را به خاطر بسپارید:
- تمام مخرج ها و اعداد باید یا از طریق فرمول های ضرب اختصاری یا از طریق یک ممیز فاکتور شوند.
- شما باید طبق الگوریتم زیر کار کنید: وقتی ما نگاه می کنیم و سعی می کنیم فرمول ضرب اختصاری را جدا کنیم، اول از همه سعی می کنیم همه چیز را به بالاترین درجه ممکن تبدیل کنیم. پس از این، درجه کلی را از براکت خارج می کنیم.
- اغلب اوقات با عباراتی با یک پارامتر روبرو می شوید: متغیرهای دیگر به عنوان ضرایب ظاهر می شوند. ما آنها را با استفاده از فرمول بسط درجه دوم پیدا می کنیم.
بنابراین، هنگامی که کسرهای گویا را می بینید، اولین کاری که باید انجام دهید این است که با استفاده از ضرب اختصاری یا فرمول های متمایز، صورت و مخرج را در عبارات خطی قرار دهید.
بیایید به چند مورد از این عبارات عقلانی نگاه کنیم و سعی کنیم آنها را فاکتور بگیریم.
حل مثال های پیچیده تر
وظیفه شماره 1
\[\frac(4((x)^(2))-6xy+9((y)^(2)))(2x-3y)\cdot \frac(9((y)^(2))- 4((x)^(2)))(8((x)^(3))+27((y)^(3)))\]
ما بازنویسی می کنیم و سعی می کنیم هر عبارت را تجزیه کنیم:
بیایید کل بیان عقلانی خود را با در نظر گرفتن این حقایق بازنویسی کنیم:
\[\frac(((\left(2x \راست))^(2))-2x\cdot 3y+((\left(3y \راست))^(2)))(2x-3y)\cdot \frac (((\left(3y \راست))^(2))-((\left(2x \راست))^(2)))((\left(2x \راست))^(3))+ ((\left(3y \راست))^(3)))=\]
\[=\frac(((\left(2x \راست))^(2))-2x\cdot 3y+((\left(3y \راست))^(2))(2x-3y)\cdot \ frac(\left(3y-2x \راست)\left(3y+2x \راست))(\left(2x+3y \راست)\left((\left(2x \راست))^(2)- 2x\cdot 3y+((\left(3y \راست))^(2)) \راست))=-1\]
پاسخ: -1 دلار.
مشکل شماره 2
\[\frac(3-6x)(2((x)^(2))+4x+8)\cdot \frac(2x+1)(((x)^(2))+4-4x)\ cdot \frac(8-((x)^(3)))(4((x)^(2))-1)\]
بیایید به همه کسری ها نگاه کنیم.
\[((x)^(2))+4-4x=((x)^(2))-4x+2=((x)^(2))-2\cdot 2x+((2)^( 2))=((\چپ(x-2 \راست))^(2))\]
بیایید کل ساختار را با در نظر گرفتن تغییرات بازنویسی کنیم:
\[\frac(3\left(1-2x \راست))(2\left(((x)^(2))+2x+((2)^(2)) \راست))\cdot \frac( 2x+1)(((\left(x-2 \راست))^(2))\cdot \frac(\left(2-x \right)\left(((2)^(2))+ 2x+((x)^(2)) \راست))(\چپ(2x-1 \راست)\چپ(2x+1 \راست))=\]
\[=\frac(3\cdot \left(-1 \right))(2\cdot \left(x-2 \right)\cdot \left(-1 \right))=\frac(3)(2 \چپ(x-2 \راست))\]
پاسخ: $\frac(3)(2\left(x-2 \راست))$.
تفاوت های ظریف راه حل
بنابراین چیزی که ما تازه یاد گرفتیم:
- هر مثلث مربعی را نمی توان فاکتور گرفت؛ به ویژه، این امر در مورد مجذور ناقص مجموع یا تفاضل، که اغلب به عنوان قطعاتی از مجموع یا مکعب تفاضل یافت می شوند، صدق می کند.
- ثابت ها، یعنی اعداد معمولی که دارای متغیر نیستند نیز می توانند به عنوان عناصر فعال در فرآیند بسط عمل کنند. اولاً می توان آنها را از براکت خارج کرد و ثانیاً خود ثابت ها را می توان در قالب توان نشان داد.
- اغلب اوقات، پس از فاکتورگیری همه عناصر، ساختارهای متضاد ایجاد می شود. این کسرها باید با دقت بسیار کاهش یابد، زیرا هنگام عبور از آنها در بالا یا پایین، یک عامل اضافی $-1$ ظاهر می شود - این دقیقاً نتیجه این واقعیت است که آنها متضاد هستند.
حل مسائل پیچیده
\[\frac(27((a)^(3))-64((b)^(3)))(((b)^(2))-4):\frac(9(((a)^ (2))+12ab+16((b)^(2)))(((ب)^(2))+4b+4)\]
بیایید هر اصطلاح را جداگانه در نظر بگیریم.
کسر اول:
\[((\left(3a \راست))^(3))-((\left(4b \راست))^(3))=\left(3a-4b \راست)\چپ(((\چپ (3a \راست))^(2))+3a\cdot 4b+((\چپ(4b \راست))^(2)) \راست)\]
\[((b)^(2))-((2)^(2))=\چپ(b-2 \راست)\چپ(b+2 \راست)\]
میتوانیم کل کسر کسر دوم را به صورت زیر بازنویسی کنیم:
\[((\left(3a \راست))^(2))+3a\cdot 4b+((\left(4b \راست))^(2))\]
حال بیایید مخرج را بررسی کنیم:
\[((b)^(2))+4b+4=((b)^(2))+2\cdot 2b+((2)^(2))=((\چپ(b+2 \راست ))^(2))\]
بیایید کل عبارت منطقی را با در نظر گرفتن حقایق فوق بازنویسی کنیم:
\[\frac(\left(3a-4b \right)\left(((\left(3a \راست))^(2))+3a\cdot 4b+((\left(4b \راست))^(2 ( ((\left(3a \راست))^(2))+3a\cdot 4b+((\left(4b \راست))^(2)))=\]
\[=\frac(\چپ(3a-4b \راست)\چپ(b+2 \راست))(\چپ(b-2 \راست))\]
پاسخ: $\frac(\left(3a-4b \راست)\left(b+2 \راست))(\left(b-2 \راست))$.
تفاوت های ظریف راه حل
همانطور که یک بار دیگر دیدیم، مربع های ناقص مجموع یا مربع های ناقص تفاوت، که اغلب در عبارات منطقی واقعی یافت می شوند، از آنها نترسید، زیرا پس از تبدیل هر عنصر تقریباً همیشه لغو می شوند. علاوه بر این، به هیچ وجه نباید در پاسخ نهایی از ساخت و سازهای بزرگ ترسید - کاملاً ممکن است که این اشتباه شما نباشد (مخصوصاً اگر همه چیز فاکتورگیری شود) اما نویسنده چنین پاسخی را در نظر گرفته است.
در پایان، می خواهم به مثال پیچیده دیگری نگاه کنم که دیگر مستقیماً به کسرهای گویا مربوط نمی شود، اما حاوی همه چیزهایی است که در آزمون ها و امتحانات واقعی در انتظار شماست، یعنی: فاکتورسازی، کاهش به مخرج مشترک، کاهش اصطلاحات مشابه. این دقیقاً همان کاری است که ما اکنون انجام خواهیم داد.
حل یک مشکل پیچیده ساده سازی و تبدیل عبارات منطقی
\[\left(\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3) )-8)-\frac(1)(x-2) \راست)\cdot \left(\frac(((x)^(2)))(((x)^(2))-4)- \frac(2)(2-x) \راست)\]
ابتدا به براکت اول نگاه می کنیم و باز می کنیم: در آن سه کسر مجزا با مخرج های مختلف می بینیم، بنابراین اولین کاری که باید انجام دهیم این است که هر سه کسر را به یک مخرج مشترک برسانیم و برای انجام این کار، هر کدام از آنها باید فاکتور گرفته شده:
\[((x)^(2))+2x+4=((x)^(2))+2\cdot x+((2)^(2))\]
\[((x)^(2))-8=((x)^(3))-((2)^(2))=\چپ(x-2 \راست)\چپ(((x) ^(2))+2x+((2)^(2)) \راست)\]
بیایید کل ساخت خود را به صورت زیر بازنویسی کنیم:
\[\frac(x)(((x)^(2))+2x+((2)^(2)))+\frac(((x)^(2))+8)(\چپ(x) -2 \right)\left(((x)^(2))+2x+((2)^(2)) \راست))-\frac(1)(x-2)=\]
\[=\frac(x\چپ(x-2 \راست)+((x)^(3))+8-\چپ(((x)^(2))+2x+((2)^(2 )) \راست))(\چپ(x-2 \راست)\چپ(((x)^(2))+2x+((2)^(2)) \راست))=\]
\[=\frac(((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\چپ(x-2) \right)\left(((x)^(2))+2x+((2)^(2)) \راست))=\frac(((x)^(2))-4x-4)(\ چپ(x-2 \right)\left(((x)^(2))+2x+((2)^(2)) \راست))=\]
\[=\frac(((\left(x-2 \راست))^(2)))(\left(x-2 \right)\left(((x)^(2))+2x+(( 2)^(2)) \راست))=\frac(x-2)(((x)^(2))+2x+4)\]
این نتیجه محاسبات براکت اول است.
بیایید به براکت دوم بپردازیم:
\[((x)^(2))-4=((x)^(2))-((2)^(2))=\چپ(x-2 \راست)\چپ(x+2 \ درست)\]
بیایید براکت دوم را با در نظر گرفتن تغییرات بازنویسی کنیم:
\[\frac(((x)^(2)))(\left(x-2 \right)\left(x+2 \right))+\frac(2)(x-2)=\frac( ((x)^(2))+2\چپ(x+2 \راست))(\چپ(x-2 \راست)\چپ(x+2 \راست))=\frac(((x)^ (2))+2x+4)(\چپ(x-2 \راست)\چپ(x+2 \راست))\]
حالا بیایید کل ساختار اصلی را بنویسیم:
\[\frac(x-2)(((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2 \راست)\چپ(x+2 \راست))=\frac(1)(x+2)\]
پاسخ: $\frac(1)(x+2)$.
تفاوت های ظریف راه حل
همانطور که می بینید، پاسخ کاملاً منطقی بود. با این حال، لطفاً توجه داشته باشید: اغلب در چنین محاسباتی در مقیاس بزرگ، زمانی که تنها متغیر فقط در مخرج ظاهر می شود، دانش آموزان فراموش می کنند که این مخرج است و باید در پایین کسر باشد و این عبارت را در صورت می نویسند - این یک اشتباه فاحش است
علاوه بر این، توجه ویژه شما را به نحوه رسمی شدن چنین وظایفی جلب می کنم. در هر محاسبات پیچیده، تمام مراحل یک به یک انجام می شود: ابتدا براکت اول را جداگانه می شماریم، سپس دومی را جداگانه می شماریم و فقط در انتها همه قسمت ها را با هم ترکیب می کنیم و نتیجه را محاسبه می کنیم. به این ترتیب، ما خود را در برابر اشتباهات احمقانه بیمه می کنیم، تمام محاسبات را با دقت یادداشت می کنیم و در عین حال، همانطور که در نگاه اول به نظر می رسد، وقت اضافی را تلف نمی کنیم.
شما نیاز خواهید داشت
- - مفهوم یک جمله چند جمله ای؛
- - فرمول ضرب مختصر؛
- - عملیات با کسری؛
- - هویت های مثلثاتی اساسی
دستورالعمل ها
اگر عبارت دارای تک جملاتی با . برای مثال، اگر عبارت 2 a-4 a+5 a+a=(2-4+5+1)∙a=4∙a وجود داشته باشد.
اگر عبارت یک کسر طبیعی است، عامل مشترک را از صورت و مخرج انتخاب کرده و کسر را با آن کاهش دهید. به عنوان مثال، اگر باید کسر (3 a²-6 a b+3 b²)/(6∙a²-6∙b²) را کاهش دهید، فاکتورهای مشترک را از صورت حذف کنید و مخرج در صورت 3 خواهد بود، در مخرج 6. عبارت (3 (a²-2 a b+b²))/(6∙(a²-b²)) را بدست آورید. صورت و مخرج را 3 کاهش دهید و فرمول ضرب اختصاری را روی عبارات باقی مانده اعمال کنید. برای صورت، مجذور اختلاف و برای مخرج، اختلاف مربع ها است. عبارت (a-b)²/(2∙ (a+b)∙(a-b)) را با کاهش آن توسط ضریب مشترک a-b بدست آورید، عبارت (a-b)/(2∙ (a+b)) را بدست آورید. برای مقادیر خاص تعداد متغیرها بسیار آسان تر است.
اگر یکجملهها فاکتورهای یکسانی دارند که به یک توان میآیند، هنگام جمع کردن آنها، مطمئن شوید که توانها برابر هستند، در غیر این صورت نمیتوان موارد مشابه را کاهش داد. برای مثال، اگر عبارت 2∙m²+6 m³-m²-4 m³+7 وجود داشته باشد، هنگامی که موارد مشابه با هم ترکیب شوند، نتیجه m²+2 m³+7 خواهد بود.
هنگام ساده سازی هویت های مثلثاتی، از فرمول ها برای تبدیل آنها استفاده کنید. هویت مثلثاتی پایه sin²(x)+cos²(x)=1، sin(x)/cos(x)=tg(x)، 1/ tg(x)= ctg(x)، فرمول های مجموع و تفاضل آرگومان ها ، استدلال دوگانه، سه گانه و دیگران. به عنوان مثال، (sin(2∙x)- cos(x))/ ctg(x). فرمول آرگومان دوگانه و کوتانژانت را به صورت نسبت کسینوس به سینوس بنویسید. دریافت (2∙ sin(x) cos(x)- cos(x)) sin(x)/cos(x). عامل مشترک cos(x) را خارج کرده و کسر cos(x) (2∙ sin(x) - 1) sin(x)/cos(x)= (2∙ sin(x) - 1) sin( ایکس).
ویدئو در مورد موضوع
منابع:
- فرمول ساده سازی بیان
کوتاهی به قول خودشان خواهر استعداد است. همه می خواهند استعدادشان را به رخ بکشند، اما خواهرش چیز پیچیده ای است. بنا به دلایلی، افکار درخشان به طور طبیعی شکل جملات پیچیده با عبارات قید زیادی را به خود می گیرند. با این حال، این شما هستید که جملات خود را ساده کنید و آنها را برای همه قابل درک و در دسترس قرار دهید.
دستورالعمل ها
برای سهولت کار برای گیرنده (اعم از شنونده یا خواننده)، سعی کنید عبارات مشارکتی و مشارکتی را با جملات فرعی کوتاه جایگزین کنید، به خصوص اگر تعداد عبارات فوق در یک جمله بیش از حد باشد. "گربه ای که به خانه آمد، به تازگی موش را خورده بود، با صدای بلند خرخر کرد، صاحبش را نوازش کرد، سعی کرد به چشمان او نگاه کند، به این امید که ماهی های آورده شده از فروشگاه را التماس کند" - این کار نمی کند. چنین ساختاری را به چند قسمت تقسیم کنید، وقت بگذارید و سعی نکنید همه چیز را در یک جمله بگویید، خوشحال خواهید شد.
اگر یک عبارت درخشان را تصور کرده اید، اما معلوم شد که بندهای فرعی زیادی دارد (مخصوصاً با یکی)، بهتر است این عبارت را به چندین جمله جداگانه تقسیم کنید یا برخی از عناصر را حذف کنید. "ما تصمیم گرفتیم که او به مارینا واسیلیونا بگوید ، که کاتیا به ویتا بگوید که ..." - می توانیم بی پایان ادامه دهیم. در زمان توقف کنید و به یاد داشته باشید که چه کسی این را می خواند یا گوش می دهد.
با این حال، مشکلات تنها در ساختار جمله نهفته است. به دایره لغات توجه کنید. کلمات خارجی، اصطلاحات طولانی، کلمات برگرفته از داستان های قرن 19 - همه اینها فقط درک را پیچیده می کند. لازم است خودتان مشخص کنید که متن را برای چه مخاطبی مینویسید: البته متخصصان فناوری هم اصطلاحات پیچیده و هم کلمات خاص را درک میکنند. اما اگر همین کلمات را به یک معلم ادبیات بگویید، بعید است که او شما را درک کند.
استعداد چیز بزرگی است. اگر با استعداد هستید (و هیچ آدمی بدون توانایی وجود ندارد)، راه های زیادی پیش روی شما باز می شود. اما استعداد در پیچیدگی نیست، بلکه در سادگی نهفته است، به اندازه کافی عجیب. آن را ساده نگه دارید، و استعدادهای شما برای همه روشن و قابل دسترس خواهد بود.
ویدئو در مورد موضوع
یادگیری ساده سازی عبارات در ریاضیات به منظور حل صحیح و سریع مسائل و معادلات مختلف ضروری است. سادهسازی یک عبارت شامل کاهش تعداد مراحل است که محاسبات را آسانتر میکند و در زمان صرفهجویی میکند.

دستورالعمل ها
یادگیری محاسبه توان های c. با ضرب توان های c عددی به دست می آید که پایه آن یکسان است و توان ها b^m+b^n=b^(m+n) جمع می شوند. هنگام تقسیم توان ها با پایه های یکسان، توان عددی به دست می آید که پایه آن ثابت می ماند و توان های توان ها کم می شود و توان مقسوم علیه b^m از توان تقسیمی کم می شود. : b^n=b^(m-n). هنگام افزایش توان به توان، توان یک عدد به دست می آید که پایه آن ثابت می ماند و توان ها ضرب می شوند (b^m)^n=b^(mn) هنگام افزایش به توان، هر عامل (abc)^m=a^m *b^m*c^m
چند جمله ای های عاملی، یعنی آنها را به عنوان محصول چندین عامل - چند جمله ای و تک جمله ای تصور کنید. فاکتور مشترک را از پرانتز خارج کنید. فرمول های ضرب خلاصه شده اصلی را بیاموزید: تفاوت مربع ها، مجموع مجذور، اختلاف مجذور، مجموع مکعب ها، تفاوت مکعب ها، مکعب مجموع و تفاوت. برای مثال، m^8+2*m^4*n^4+n^8=(m^4)^2+2*m^4*n^4+(n^4)^2. این فرمول ها اصلی ترین فرمول ها در ساده سازی عبارات هستند. از روش جداسازی مربع کامل در یک مثلثی به شکل ax^2+bx+c استفاده کنید.
کسری ها را تا حد امکان مخفف کنید. برای مثال، (2*a^2*b)/(a^2*b*c)=2/(a*c). اما به یاد داشته باشید که شما فقط می توانید چند برابر را کاهش دهید. اگر صورت و مخرج کسر جبری در عددی غیر از صفر ضرب شود، مقدار کسر تغییر نخواهد کرد. دو راه برای تبدیل عبارات عقلانی وجود دارد: زنجیره ای و عملی. روش دوم ارجح است، زیرا بررسی نتایج اقدامات میانی آسانتر است.
اغلب نیاز به استخراج ریشه در عبارات است. حتی ریشه ها فقط از عبارات یا اعداد غیر منفی استخراج می شوند. ریشه های فرد را می توان از هر عبارتی استخراج کرد.
منابع:
- ساده سازی عبارات با قدرت
«بیان» در ریاضیات معمولاً به مجموعهای از عملیاتهای حسابی و جبری اطلاق میشود که شامل اعداد و مقادیر متغیر است. با قیاس با فرمت نوشتن اعداد، چنین مجموعه ای در صورتی که شامل عملیات تقسیم باشد، "کسری" نامیده می شود. عملیات ساده سازی برای عبارات کسری و همچنین برای اعداد در قالب کسری اعمال می شود.

دستورالعمل ها
با یافتن ضریب مشترک برای , ایستاده در صورتگر و - این برای هر دو نسبت عددی و آنهایی که حاوی متغیرهای ناشناخته هستند یکسان است. برای مثال، اگر صورت 45*X و مخرج آن 18*Y باشد، بزرگترین ضریب مشترک 9 است. پس از اتمام این مرحله، صورت را می توان به صورت 9*5*X و مخرج را 9*2* نوشت. Y.
اگر عبارات موجود در صورت و مخرج ترکیبی از عملیات ریاضی پایه (، تقسیم، جمع و تفریق) باشد، ابتدا باید ضریب مشترک را برای هر یک از آنها به طور جداگانه محاسبه کنید و سپس بزرگترین عامل مشترک را از آنها جدا کنید. شماره. مثلاً برای عبارت 45*X+180 که در صورتگر است باید ضریب 45 را از پرانتز خارج کرد: 45*X+180 = 45*(X+4). و عبارت 18+54*Y در مخرج باید به شکل 18*(1+3*Y) کاهش یابد. سپس مانند مرحله قبل، بزرگترین مقسوم علیه مشترک عوامل خارج شده از پرانتز را پیدا کنید: 45*X+180 / 18+54*Y = 45*(X+4) / 18*(1+3*Y) = 9*5* (X+4) / 9*2*(1+3*Y). در این مثال نیز برابر با نه است.
ضریب مشترک عبارات موجود در صورت و مخرج کسری که در مراحل قبل یافت شد را کاهش دهید. برای مثال از مرحله اول، کل عملیات ساده سازی را می توان به صورت زیر نوشت: 45*X / 18*Y = 9*5*X / 9*2*Y = 5*X / 2*Y.
هنگام ساده کردن، مقسوم علیه مشترک نباید عددی باشد، بلکه می تواند عبارتی حاوی یک متغیر باشد. به عنوان مثال، اگر صورت کسری (4*X + X*Y + 12 + 3*Y) و مخرج آن (X*Y + 3*Y - 7*X - 21) باشد، بزرگترین مشترک مقسومکننده عبارت X+ 3 خواهد بود که برای سادهسازی عبارت باید آن را کاهش داد: (4*X + X*Y + 12 + 3*Y) / (X*Y + 3*Y - 7*X - 21) = ( X+3)*(4 +Y) / (X+3)*(Y-7) = (4+Y) / (Y-7).
حفظ حریم خصوصی شما برای ما مهم است. به همین دلیل، ما یک خط مشی رازداری ایجاد کرده ایم که نحوه استفاده و ذخیره اطلاعات شما را شرح می دهد. لطفاً رویههای حفظ حریم خصوصی ما را مرور کنید و اگر سؤالی دارید با ما در میان بگذارید.
جمع آوری و استفاده از اطلاعات شخصی
اطلاعات شخصی به داده هایی اشاره دارد که می توان از آنها برای شناسایی یا تماس با یک فرد خاص استفاده کرد.
ممکن است در هر زمانی که با ما تماس می گیرید از شما خواسته شود اطلاعات شخصی خود را ارائه دهید.
در زیر چند نمونه از انواع اطلاعات شخصی که ممکن است جمع آوری کنیم و نحوه استفاده از این اطلاعات آورده شده است.
چه اطلاعات شخصی جمع آوری می کنیم:
- هنگامی که درخواستی را در سایت ارسال می کنید، ممکن است اطلاعات مختلفی از جمله نام، شماره تلفن، آدرس ایمیل و غیره شما را جمع آوری کنیم.
نحوه استفاده ما از اطلاعات شخصی شما:
- اطلاعات شخصی که جمع آوری می کنیم به ما امکان می دهد با پیشنهادات منحصر به فرد، تبلیغات و سایر رویدادها و رویدادهای آینده با شما تماس بگیریم.
- هر از گاهی، ممکن است از اطلاعات شخصی شما برای ارسال اعلانها و ارتباطات مهم استفاده کنیم.
- ما همچنین ممکن است از اطلاعات شخصی برای مقاصد داخلی مانند انجام ممیزی، تجزیه و تحلیل داده ها و تحقیقات مختلف به منظور بهبود خدمات ارائه شده و ارائه توصیه هایی در مورد خدمات خود به شما استفاده کنیم.
- اگر در قرعه کشی جوایز، مسابقه یا تبلیغات مشابه شرکت می کنید، ممکن است از اطلاعاتی که شما ارائه می دهید برای اجرای چنین برنامه هایی استفاده کنیم.
افشای اطلاعات به اشخاص ثالث
ما اطلاعات دریافتی از شما را در اختیار اشخاص ثالث قرار نمی دهیم.
استثناها:
- در صورت لزوم - مطابق با قانون، رویه قضایی، در مراحل قانونی و / یا بر اساس درخواست های عمومی یا درخواست های ارگان های دولتی در فدراسیون روسیه - اطلاعات شخصی خود را افشا کنید. همچنین اگر تشخیص دهیم که چنین افشایی برای اهداف امنیتی، اجرای قانون یا سایر اهداف مهم عمومی ضروری یا مناسب است، ممکن است اطلاعاتی درباره شما فاش کنیم.
- در صورت سازماندهی مجدد، ادغام یا فروش، ممکن است اطلاعات شخصی را که جمع آوری می کنیم به شخص ثالث جانشین مربوطه منتقل کنیم.
حفاظت از اطلاعات شخصی
ما اقدامات احتیاطی - از جمله اداری، فنی و فیزیکی - را برای محافظت از اطلاعات شخصی شما در برابر از دست دادن، سرقت، و سوء استفاده، و همچنین دسترسی غیرمجاز، افشا، تغییر و تخریب انجام می دهیم.
احترام به حریم خصوصی شما در سطح شرکت
برای اطمینان از ایمن بودن اطلاعات شخصی شما، استانداردهای حریم خصوصی و امنیتی را به کارمندان خود ابلاغ می کنیم و شیوه های حفظ حریم خصوصی را به شدت اجرا می کنیم.
 نمادهای عناصر شیمیایی و اصول تعیین آنها
نمادهای عناصر شیمیایی و اصول تعیین آنها تبدیل عبارات
تبدیل عبارات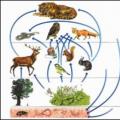 بخش IV پیوندهای زیستی در نتیجه گیری طبیعت
بخش IV پیوندهای زیستی در نتیجه گیری طبیعت