Kinematic viscosity of liquids table. Viscosity of water. Kinematic viscosity of water. Dynamic viscosity of water. Examples of problem solving
Viscosity is the most important physical constant that characterizes the performance properties of boiler and diesel fuels, petroleum oils, and a number of other petroleum products. The viscosity value is used to judge the possibility of atomization and pumpability of oil and petroleum products.
There are dynamic, kinematic, conditional and effective (structural) viscosity.
Dynamic (absolute) viscosity [μ ], or internal friction, is the property of real fluids to resist shearing tangential forces. Obviously, this property manifests itself when the fluid moves. Dynamic viscosity in the SI system is measured in [N·s/m2]. This is the resistance that a liquid exhibits during the relative movement of its two layers with a surface of 1 m2, located at a distance of 1 m from each other and moving under the influence of an external force of 1 N at a speed of 1 m/s. Given that 1 N/m 2 = 1 Pa, dynamic viscosity is often expressed in [Pa s] or [mPa s]. In the CGS system (CGS), the dimension of dynamic viscosity is [din s/m 2 ]. This unit is called poise (1 P = 0.1 Pa s).
Conversion factors for calculating dynamic [ μ ] viscosity.
| Units | Micropoise (mcP) | Centipoise (sp) | Poise ([g/cm s]) | Pa s ([kg/m s]) | kg/(m h) | kg s/m 2 |
| Micropoise (mcP) | 1 | 10 -4 | 10 -6 | 10 7 | 3.6·10 -4 | 1.02·10 -8 |
| Centipoise (sp) | 10 4 | 1 | 10 -2 | 10 -3 | 3,6 | 1.02·10 -4 |
| Poise ([g/cm s]) | 10 6 | 10 2 | 1 | 10 3 | 3.6 10 2 | 1.02·10 -2 |
| Pa s ([kg/m s]) | 10 7 | 10 3 | 10 | 1 3 | 3.6 10 3 | 1.02·10 -1 |
| kg/(m h) | 2.78 10 3 | 2.78·10 -1 | 2.78·10 -3 | 2.78·10 -4 | 1 | 2.84·10 -3 |
| kg s/m 2 | 9.81 10 7 | 9.81 10 3 | 9.81 10 2 | 9.81 10 1 | 3.53 10 4 | 1 |
Kinematic viscosity [ν ] is a quantity equal to the ratio of the dynamic viscosity of the liquid [ μ ] to its density [ ρ ] at the same temperature: ν = μ/ρ. The unit of kinematic viscosity is [m 2 /s] - the kinematic viscosity of such a liquid, the dynamic viscosity of which is 1 N s / m 2 and the density is 1 kg / m 3 (N = kg m / s 2). In the CGS system, kinematic viscosity is expressed in [cm 2 /s]. This unit is called Stokes (1 Stokes = 10 -4 m 2 /s; 1 cSt = 1 mm 2 /s).
Conversion factors for calculating kinematic [ ν ] viscosity.
| Units | mm 2 /s (cSt) | cm 2 /s (St) | m 2 /s | m 2 /h |
| mm 2 /s (cSt) | 1 | 10 -2 | 10 -6 | 3.6·10 -3 |
| cm 2 /s (St) | 10 2 | 1 | 10 -4 | 0,36 |
| m 2 /s | 10 6 | 10 4 | 1 | 3.6 10 3 |
| m 2 /h | 2.78 10 2 | 2,78 | 2.78 10 4 | 1 |
Oils and petroleum products are often characterized conditional viscosity, which is taken to be the ratio of the flow time of 200 ml of petroleum product through the calibrated hole of a standard viscometer at a certain temperature [ t] by the time 200 ml of distilled water has flowed at a temperature of 20°C. Conditional viscosity at temperature [ t] is indicated by the sign ВУ, and is expressed by the number of conventional degrees.
Conditional viscosity is measured in degrees VU (°VU) (if the test is carried out in a standard viscometer according to GOST 6258-85), Saybolt seconds and Redwood seconds (if the test is carried out on Saybolt and Redwood viscometers).
You can convert viscosity from one system to another using a nomogram.
In petroleum dispersed systems under certain conditions, unlike Newtonian liquids, viscosity is a variable value depending on the shear rate gradient. In these cases, oils and petroleum products are characterized by effective or structural viscosity:
For hydrocarbons, viscosity depends significantly on their chemical composition: it increases with increasing molecular weight and boiling point. The presence of side branches in the molecules of alkanes and naphthenes and an increase in the number of cycles also increase viscosity. For different groups of hydrocarbons, viscosity increases in the series alkanes - arenes - cyclanes.
To determine viscosity, special standard instruments are used - viscometers, which differ in their operating principle.
Kinematic viscosity is determined for relatively low-viscosity light petroleum products and oils using capillary viscometers, the action of which is based on the fluidity of the liquid through the capillary in accordance with GOST 33-2000 and GOST 1929-87 (viscometer type VPZh, Pinkevich, etc.).
For viscous petroleum products, the relative viscosity is measured in viscometers such as VU, Engler, etc. The liquid flows out of these viscometers through a calibrated hole in accordance with GOST 6258-85.
There is an empirical relationship between the values of conditional °VV and kinematic viscosity:
The viscosity of the most viscous, structured petroleum products is determined on a rotational viscometer according to GOST 1929-87. The method is based on measuring the force required to rotate the inner cylinder relative to the outer one when filling the space between them with the test liquid at a temperature t.
In addition to standard methods for determining viscosity, sometimes in research works non-standard methods are used, based on measuring viscosity by the time of falling of a calibration ball between marks or by the time of damping of vibrations of a solid body in the test liquid (Heppler, Gurvich viscometers, etc.).
In all the described standard methods, viscosity is determined at a strictly constant temperature, since with its change the viscosity changes significantly.
Dependence of viscosity on temperature
The dependence of the viscosity of petroleum products on temperature is a very important characteristic both in oil refining technology (pumping, heat exchange, sedimentation, etc.) and in the use of commercial petroleum products (draining, pumping, filtering, lubrication of rubbing surfaces, etc.).
As the temperature decreases, their viscosity increases. The figure shows curves of changes in viscosity depending on temperature for various lubricating oils.
Common to all oil samples is the presence of temperature regions in which a sharp increase in viscosity occurs.
There are many different formulas for calculating viscosity depending on temperature, but the most commonly used is Walther's empirical formula:
Taking the logarithm of this expression twice, we get:
Using this equation, E. G. Semenido compiled a nomogram on the abscissa axis of which, for ease of use, temperature is plotted, and viscosity is plotted on the ordinate axis.
Using the nomogram, you can find the viscosity of a petroleum product at any given temperature if its viscosity at two other temperatures is known. In this case, the value of the known viscosities is connected by a straight line and continued until it intersects with the temperature line. The point of intersection with it corresponds to the desired viscosity. The nomogram is suitable for determining the viscosity of all types of liquid petroleum products.
For petroleum lubricating oils, it is very important during operation that the viscosity depends as little as possible on temperature, since this ensures good lubricating properties of the oil over a wide temperature range, i.e., in accordance with the Walther formula, this means that for lubricating oils, the lower the coefficient B, the higher the quality of the oil. This property of oils is called viscosity index, which is a function of the chemical composition of the oil. For different hydrocarbons, viscosity changes differently with temperature. The steepest dependence (large value of B) is for aromatic hydrocarbons, and the smallest for alkanes. Naphthenic hydrocarbons in this respect are close to alkanes.
There are various methods for determining the viscosity index (VI).
In Russia, IV is determined by two values of kinematic viscosity at 50 and 100°C (or at 40 and 100°C - according to a special table of the State Committee of Standards).
When certifying oils, IV is calculated according to GOST 25371-97, which provides for determining this value by viscosity at 40 and 100°C. According to this method, according to GOST (for oils with VI less than 100), the viscosity index is determined by the formula:
For all oils with ν 100 ν, ν 1 And ν 3) are determined according to the GOST 25371-97 table based on ν 40 And ν 100 of this oil. If the oil is more viscous ( ν 100> 70 mm 2 /s), then the values included in the formula are determined using special formulas given in the standard.
It is much easier to determine the viscosity index using nomograms.
An even more convenient nomogram for finding the viscosity index was developed by G.V. Vinogradov. Determining IV is reduced to connecting known viscosity values at two temperatures with straight lines. The intersection point of these lines corresponds to the desired viscosity index.
Viscosity index is a generally accepted value included in oil standards in all countries of the world. The disadvantage of the viscosity index is that it characterizes the behavior of the oil only in the temperature range from 37.8 to 98.8 ° C.
Many researchers have noted that the density and viscosity of lubricating oils to some extent reflect their hydrocarbon composition. A corresponding indicator was proposed linking the density and viscosity of oils and called the viscosity-mass constant (VMC). The viscosity-mass constant can be calculated using the formula of Yu. A. Pinkevich:
Depending on the chemical composition of the VMC oil, it can be from 0.75 to 0.90, and the higher the VMC of the oil, the lower its viscosity index.
At low temperatures, lubricating oils acquire a structure that is characterized by the yield strength, plasticity, thixotropy or viscosity anomaly characteristic of dispersed systems. The results of determining the viscosity of such oils depend on their preliminary mechanical mixing, as well as on the flow rate or both factors simultaneously. Structured oils, like other structured petroleum systems, do not obey the law of Newtonian fluid flow, according to which the change in viscosity should depend only on temperature.
Oil with an intact structure has a significantly higher viscosity than after its destruction. If you reduce the viscosity of such an oil by destroying the structure, then in a calm state this structure will be restored and the viscosity will return to its original value. The ability of a system to spontaneously restore its structure is called thixotropy. With an increase in the flow speed, or more precisely the speed gradient (section of curve 1), the structure is destroyed, and therefore the viscosity of the substance decreases and reaches a certain minimum. This minimum viscosity remains at the same level with a subsequent increase in the velocity gradient (section 2) until a turbulent flow appears, after which the viscosity increases again (section 3).
Dependence of viscosity on pressure
The viscosity of liquids, including petroleum products, depends on external pressure. The change in oil viscosity with increasing pressure is of great practical importance, since high pressures can arise in some friction units.
The dependence of viscosity on pressure for some oils is illustrated by curves; the viscosity of oils changes parabolically with increasing pressure. Under pressure R it can be expressed by the formula:
In petroleum oils, the viscosity of paraffin hydrocarbons changes least with increasing pressure, and naphthenic and aromatic hydrocarbons change slightly more. The viscosity of high-viscosity petroleum products increases with increasing pressure more than the viscosity of low-viscosity petroleum products. The higher the temperature, the less the viscosity changes with increasing pressure.
At pressures of the order of 500 - 1000 MPa, the viscosity of oils increases so much that they lose the properties of a liquid and turn into a plastic mass.
To determine the viscosity of petroleum products at high pressure, D.E. Mapston proposed the formula:
Based on this equation, D.E. Mapston developed a nomogram, using which known values, for example ν 0 And R, are connected by a straight line and the reading is obtained on the third scale.
Viscosity of mixtures
When compounding oils, it is often necessary to determine the viscosity of mixtures. As experiments have shown, additivity of properties manifests itself only in mixtures of two components that are very close in viscosity. When there is a large difference in the viscosities of the petroleum products being mixed, the viscosity is usually less than that calculated by the mixing rule. The viscosity of an oil mixture can be approximately calculated by replacing the viscosities of the components with their reciprocal values - mobility (fluidity) ψ cm:
To determine the viscosity of mixtures, you can also use various nomograms. The most widely used are the ASTM nomogram and the Molina-Gurvich viscosigram. The ASTM nomogram is based on the Walther formula. The Molina-Gurevich nomogram was compiled on the basis of the experimentally found viscosities of a mixture of oils A and B, of which A has a viscosity °ВУ 20 = 1.5, and B has a viscosity °ВУ 20 = 60. Both oils were mixed in different ratios from 0 to 100% (vol.), and the viscosity of the mixtures was established experimentally. The nomogram shows the viscosity values in el. units and in mm 2 /s.
Viscosity of gases and oil vapors
The viscosity of hydrocarbon gases and oil vapors is subject to different laws than for liquids. With increasing temperature, the viscosity of gases increases. This pattern is satisfactorily described by the Sutherland formula:
Water H 2 O is a Newtonian fluid and its flow is described by Newton's law of viscous friction, in the equation of which the proportionality coefficient is called the viscosity coefficient, or simply viscosity.
The viscosity of water depends on temperature. The kinematic viscosity of water is 1.006·10 -6 m 2 /s at a temperature of 20°C.
The table shows the values of the kinematic viscosity of water depending on temperature at atmospheric pressure (760 mm Hg). Viscosity values are given in the temperature range from 0 to 300°C. At water temperatures above 100°C, its kinematic viscosity is indicated in the table on the saturation line.
The kinematic viscosity of water changes its value when heated and cooled. According to the table it is clear that As the water temperature increases, its kinematic viscosity decreases. If we compare the viscosity of water at different temperatures, for example at 0 and 300°C, then it is obvious that it decreases by about 14 times. That is, water becomes less viscous when heated, and high viscosity of water is achieved if the water is cooled as much as possible.
The values of the coefficient of kinematic viscosity at different temperatures are necessary to calculate the value of the Reynolds number, which corresponds to a certain flow regime of a liquid or gas.
If we compare the viscosity of water with the viscosity of other Newtonian fluids, for example with, or with, then water will have a lower viscosity. Less viscous than water are organic liquids - benzene and liquefied gases, for example, such as.
Dynamic viscosity of water depending on temperature
Kinematic and dynamic viscosity are related to each other through the density value. If kinematic viscosity is multiplied by density, we obtain the value of the coefficient of dynamic viscosity (or simply dynamic viscosity).
The dynamic viscosity of water at a temperature of 20°C is 1004·10 -6 Pa·s. The table shows the values of the coefficient of dynamic viscosity of water depending on temperature at normal atmospheric pressure (760 mm Hg). The viscosity in the table is indicated at temperatures from 0 to 300°C.
Dynamic viscosity decreases when water is heated, water becomes less viscous and when it reaches
Before talking about the properties of water, it is worth understanding the very concept of “water”. It is a transparent liquid, which in most cases has no characteristic color or odor. When water changes into something else, it forms derivatives called ice, snow (solid state) or steam (gaseous state). It is believed that it covers more than 70% of the surface of planet Earth - all kinds of seas and oceans, rivers, lakes, glaciers and other hydrological objects.
Water is a strong solvent, which in natural conditions contains many mineral salts and various gases. If we talk about its physical properties, we will immediately pay attention to the fact that when ice melts, its density increases, while for other substances a similar process occurs exactly the opposite.
The main feature of water is viscosity. Viscosity itself is the ability of a substance (be it a liquid, gas or solid) to exert resistance between particles of the substance relative to each other. This characteristic can be of two types - volumetric and tangential. Bulk viscosity is the ability of a substance to accept tensile force. It manifests itself when sound or ultrasonic waves propagate in water. Tangential viscosity is characterized by the ability of a fluid to resist shearing force.
When scientists studied the viscosity of water, it was found that the resistance of the substance during stretching and shearing depends on the speed of movement of particles in different layers of the liquid. If a layer that is moving faster acts on a layer that is moving slower, an accelerating force is generated. If everything happens exactly the opposite, then the braking force begins to act. The above-mentioned forces are directed tangentially to the surfaces of the layers.
Question:
Hello! Can you tell me, I can’t find it anywhere, what is the viscosity of salt water with a density of 1.15-1.2 g/cm 3 at low and negative temperatures? For example at -20 degrees Celsius? Thank you in advance. Ruslan
Answer:
Hello, dear Ruslan!
The dynamic viscosity coefficient of water strongly depends on temperature, but is almost independent of pressure. The value of this coefficient for fresh water, obtained experimentally for t°С = 0°С, μ = 1.793·10 3 Pa·s. When calculating the dynamic viscosity coefficient, the empirical Poiseuille formula is used:
μ = 0.000183/(1 + 0.0337t + 0.000221t 2),
where t is the water temperature.
The dynamic viscosity coefficient of salt water differs slightly from that of fresh water. For example, at t = 20°C and S = 25‰ it is equal to 1.052·10 -3 Pa·s, and for fresh water - 1.003·10 -3 Pa·s, i.e. more by about 5%.
It should be noted that many calculation formulas include the ratio of the dynamic viscosity coefficient μ to the liquid density ρ, which is called the kinematic viscosity coefficient (kinematic viscosity):
ν = μ/ρ
The values of viscosity coefficients decrease significantly with increasing temperature.
The viscosity of liquids can also be determined with a viscometer. There are several types of such devices. In the simplest field viscometer, based on the flow principle, for example, a test solution with a volume of 500 cm 3 is poured into a funnel, the viscosity of which must be determined. The temperature and time of flow from the funnel of the test solution T r are measured; then distilled water is poured into the funnel at the same temperature (usually 20°C) and its expiration time T is determined. Attitude
There is a relative viscosity (for viscous liquids it is always greater than 1).
The viscosity of water decreases with increasing temperature quite significantly: for example, when the temperature of water increases from 0 to 100 0 C, the viscosity decreases by about 8 times. At normal atmospheric pressure, a table has been compiled to determine the kinematic coefficient of viscosity of water depending on temperature.
Value v m 2 /s for water depending on temperature
| t°C | 0 | 2 | 4 | 6 | 8 |
| 0 | 179 | 167 | 157 | 147 | 138 |
| 10 | 131 | 124 | 117 | 112 | 106 |
| 20 | 101 | 96 | 92 | 87 | 84 |
| 30 | 80 | 75 | 72 | 69 | 67 |
| 40 | 66 | 62 | 60 | 58 | 56 |
| 50 | 56 | 52 | 51 | 49 | 48 |
In addition, the viscosity of a liquid also depends on pressure. At pressures up to 2·10 7 Pa, the change in water viscosity is insignificant and is often not taken into account in calculations.
Reference data on the dependence of water viscosity on temperature is given in the following reference books:
Rivkin S.L. Thermophysical properties of water www.oglibrary.ru/data/demo/6263/62630003.html
Directory of chemist Nikolsky B.P. lib.mexmat.ru/books/12114
Physical properties of water
Density of water at different temperatures
| Temperature | Density |
| o C | kg/m 3 |
| 0 | 999,9 |
| 5 | 1000 |
| 10 | 999,7 |
| 20 | 998,2 |
| 30 | 995,7 |
| 40 | 992,2 |
| 50 | 988,1 |
| 60 | 983,2 |
| 70 | 977,8 |
| 80 | 971,8 |
| 90 | 965,3 |
| 100 | 958,4 |
Dynamic and kinematic viscosity of water at different temperatures
| Temperature | Dynamic viscosity | Kinematic viscosity |
| o C | (N.c/m2) x 10 -3 | (m2/s) x 10 -6 |
| 0 | 1,787 | 1,787 |
| 5 | 1,519 | 1,519 |
| 10 | 1,307 | 1,307 |
| 20 | 1,002 | 1,004 |
| 30 | 0,798 | 0,801 |
| 40 | 0,653 | 0,658 |
| 50 | 0,547 | 0,658 |
| 60 | 0,467 | 0,475 |
| 70 | 0,404 | 0,413 |
| 80 | 0,355 | 0,365 |
| 90 | 0,315 | 0,326 |
| 100 | 0,282 | 0,294 |
Basic physical properties of water at different temperatures
| Temperature | Density | Specific heat capacity, C p | Coefficient of thermal linear expansion | Prandtl number |
| o C | kg/m 3 | kJ/(kg.K) | (1/K) x 10 3 | - |
| 0 | 999,9 | 4,217 | -0,07 | 13,67 |
| 20 | 998,2 | 4,182 | 0,207 | 7,01 |
| 40 | 992,1 | 4,179 | 0,385 | 4,34 |
| 60 | 983,2 | 4,185 | 0,523 | 2,99 |
| 80 | 971,8 | 4,197 | 0,643 | 2,23 |
| 100 | 958,4 | 4,216 | 0,752 | 1,75 |
DEFINITION
Viscosity called one of the types of transfer phenomena. It is associated with the property of fluid substances (gases and liquids) to resist the movement of one layer relative to another. This phenomenon is caused by the movement of particles that make up matter.
There are dynamic viscosity and kinematic viscosity.
Let us consider the movement of a gas with viscosity as the movement of flat parallel layers. We will assume that the change in the speed of movement of the substance occurs in the direction of the X axis, which is perpendicular to the direction of the speed of gas movement (Fig. 1).
In the direction of the Y axis, the speed of movement at all points is the same. This means that speed is a function of . In this case, the modulus of the friction force between the gas layers (F), which acts per unit surface area that separates two adjacent layers, is described by the equation:
where is the velocity gradient () along the X axis. The X axis is perpendicular to the direction of movement of the layers of matter (Fig. 1).
Definition
The coefficient () included in equation (1) is called the coefficient of dynamic viscosity (coefficient of internal friction). It depends on the properties of the gas (liquid). is numerically equal to the amount of motion that is transferred per unit time through a platform of unit area with a velocity gradient equal to unity, in a direction perpendicular to the site. Or is numerically equal to the force that acts per unit area with a velocity gradient equal to unity.
Internal friction is the reason why a pressure difference is required for gas (liquid) to flow through a pipe. In this case, the higher the viscosity coefficient of the substance, the greater the pressure difference must be to impart a given flow speed.
The coefficient of kinematic viscosity is usually denoted by . It is equal to:
where is the gas (liquid) density.
Gas internal friction coefficient
In accordance with the kinetic theory of gases, the viscosity coefficient can be calculated using the formula:
where is the average speed of thermal motion of gas molecules, and is the average free path of a molecule. Expression (3) shows that at low pressure (rarefied gas) viscosity is almost independent of pressure, since 
But this conclusion is valid until the ratio of the free path of the molecule to the linear dimensions of the vessel becomes approximately equal to unity. With increasing temperature, the viscosity of gases usually increases, since
Liquid viscosity coefficient
Assuming that the viscosity coefficient is determined by the interaction forces between the molecules of a substance, which depend on the average distance between them, the viscosity coefficient is determined by the experimental Baczynski formula:
where is the molar volume of the liquid, A and B are constants.
The viscosity of liquids decreases with increasing temperature and increases with increasing pressure.
Poiseuille's formula
The viscosity coefficient is included in the formula that establishes the relationship between the volume (V) of gas that flows per unit time through the pipe section and the pressure difference required for this ():
where is the length of the pipe, is the radius of the pipe.
Reynolds number
The nature of gas (liquid) movement is determined by the dimensionless Reynolds number ():
Viscosity Coefficient Units
The basic unit of measurement for the coefficient of dynamic viscosity in the SI system is:
1Pa c=10 poise
The basic unit of measurement for the coefficient of kinematic viscosity in the SI system is:
Examples of problem solving
EXAMPLE 1
| Exercise | Dynamically, the viscosity of water is equal to Pa s. What is the maximum diameter of the pipe that will allow the water flow to remain laminar if in 1 s a volume of water flows out through the cross section equal to ? |
| Solution | The condition for laminarity of fluid flow has the form: Where we find the Reynolds number using the formula:
We find the speed of water flow as: In expression (1.3) is the height of a water cylinder having a volume: According to the condition = 1 s. Substituting speed (1.4) into the expression for the Reynolds number, we have: Density of water at no. kg/m3. Let's carry out the calculations and get: |
| Answer | m |
EXAMPLE 2
| Exercise | A ball of density and diameter d floats up in a liquid of density with a speed of . What is the kinematic viscosity of the fluid? |
| Solution | Let's make a drawing. |
Insulin is the youngest hormone Whey protein and insulin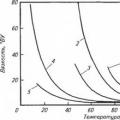
Kinematic viscosity of liquids table
Akathist to the Mother of God in front of the icon of the assistant in childbirth