Hur man beräknar den inversa matrisen. Hitta invers matris online. Använda en miniräknare

Matrix Algebra - Invers Matrix

invers matris

invers matris En matris kallas som, när den multipliceras både till höger och till vänster med en given matris, ger identitetsmatrisen.
Beteckna matrisen invers mot matrisen MEN genom , då får vi enligt definitionen:

var Eär identitetsmatrisen.
kvadratisk matris kallad icke-speciell (icke degenererad) om dess determinant inte är lika med noll. Annars heter det särskild (degenererad) eller singularis.

Det finns ett teorem: varje icke-singular matris har en invers matris.

Operationen att hitta den inversa matrisen kallas överklagande matriser. Tänk på matrisinversionsalgoritmen. Låt en icke-singular matris ges n-th order:

där Δ = det A ≠ 0.

Algebraiskt elementkomplement matriser n-:e ordningen MEN matrisens determinant ( n–1)-te ordningen erhålls genom borttagning i-th rad och j-th kolumn i matrisen MEN:

Låt oss skapa en sk bifogad matris:

var är de algebraiska komplementen av motsvarande element i matrisen MEN.
Observera att de algebraiska komplementen till radelementen i matrisen MEN placeras i motsvarande kolumner i matrisen Ã , det vill säga matrisen transponeras samtidigt.
Dela alla matriselement Ã på Δ - värdet av matrisens determinant MEN, får vi den inversa matrisen som ett resultat:

Vi noterar ett antal speciella egenskaper hos den inversa matrisen:
1) för en given matris MEN dess inversa matris är den enda;
2) om det finns en invers matris, då höger omvänd och vänster omvänd matriser sammanfaller med det;
3) en speciell (degenererad) kvadratisk matris har inte en invers matris.

Huvudegenskaperna för den inversa matrisen:
1) determinanten för den inversa matrisen och determinanten för den ursprungliga matrisen är reciproka;
2) den inversa matrisen av produkten av kvadratiska matriser är lika med produkten av de inversa matriserna av faktorer, taget i omvänd ordning:

3) den transponerade inversa matrisen är lika med den inversa matrisen från den givna transponerade matrisen:

EXEMPEL Beräkna matrisinversen av den givna.

invers matrisär en matris A -1, när den multipliceras med vilken den givna initiala matrisen A ger identitetsmatrisen E:

AA −1 = A −1 A =E.

Invers matrismetod.

Invers matrismetod- detta är en av de vanligaste metoderna för att lösa matriser och är van vid lösningar av system av linjära algebraiska ekvationer(SLAE) i de fall där antalet okända motsvarar antalet ekvationer.

Låt det finnas ett system n linjära ekvationer med n okänd:

Ett sådant system kan skrivas som en matrisekvation A*X=B,

var
- systemmatris,

- kolumn av okända,

- kolumn med fria koefficienter.

Från den härledda matrisekvationen uttrycker vi X genom att multiplicera båda sidor av matrisekvationen till vänster med A-1, resulterar i:

A -1 * A * X = A -1 * B

Veta att A-1*A=E, då E*X=A-1*B eller X=A-1*B.

Nästa steg är att bestämma den inversa matrisen A-1 och multiplicerat med kolumnen med fria termer B.

Invers matris till matris A finns bara när det A≠ 0 . Med tanke på detta, när man löser SLAE med den inversa matrismetoden, är det första steget att hitta det A. Om en det A≠ 0 , då har systemet bara en lösning, som kan erhållas med den inversa matrismetoden, if det A = 0, sedan ett sådant system invers matrismetodär inte löst.

Invers matrislösning.

Åtgärdssekvens för inversa matrislösningar:

Få matrisdeterminanten A. Om determinanten är större än noll löser vi den inversa matrisen vidare, om den är lika med noll så kan den inversa matrisen inte hittas här.
Att hitta den transponerade matrisen PÅ.
Vi letar efter algebraiska komplement, varefter vi ersätter alla element i matrisen med deras algebraiska komplement.
Vi samlar in den inversa matrisen från algebraiska tillägg: vi delar alla element i den resulterande matrisen med determinanten för den initialt givna matrisen. Den slutliga matrisen kommer att vara den önskade inversa matrisen med avseende på den ursprungliga.

Algoritmen nedan inversa matrislösningar i huvudsak samma som ovan, skillnaden är bara i några få steg: först och främst bestämmer vi de algebraiska tilläggen, och efter det beräknar vi unionsmatrisen C.

Ta reda på om den givna matrisen är kvadratisk. Vid ett negativt svar blir det tydligt att det inte kan finnas en omvänd matris för det.
Ta reda på om den givna matrisen är kvadratisk. Vid ett negativt svar blir det tydligt att det inte kan finnas en omvänd matris för det.
Vi beräknar algebraiska additioner.
Vi komponerar den allierade (ömsesidiga, bifogade) matrisen C.
Vi komponerar en invers matris från algebraiska tillägg: alla element i den adjoint matrisen C dividera med determinanten för den initiala matrisen. Den resulterande matrisen kommer att vara den önskade inversa matrisen med avseende på den givna.
Vi kontrollerar det utförda arbetet: vi multiplicerar de initiala och resulterande matriserna, resultatet ska vara identitetsmatrisen.

Detta görs bäst med en bifogad matris.

Sats: Om vi tilldelar en identitetsmatris av samma ordning till en kvadratisk matris på höger sida och omvandlar den initiala matrisen till vänster till en enhetsmatris med hjälp av elementära transformationer över rader, så kommer den som erhålls på höger sida att vara invers mot den första.

Ett exempel på att hitta den inversa matrisen.

Träning. För matris hitta inversen genom adjoint matrismetoden.

Beslut. Vi lägger till den givna matrisen MEN till höger, identitetsmatrisen av andra ordningen:

Subtrahera 2:an från 1:a raden:

Subtrahera de första 2 från den andra raden:

Matrisen $A^(-1)$ kallas inversen av kvadratmatrisen $A$ om $A^(-1)\cdot A=A\cdot A^(-1)=E$, där $E $ är identitetsmatrisen, vars ordning är lika med ordningen för matrisen $A$.

En icke-singular matris är en matris vars determinant inte är lika med noll. Följaktligen är en degenererad matris en vars determinant är lika med noll.

Den inversa matrisen $A^(-1)$ existerar om och endast om matrisen $A$ är ickesingular. Om den inversa matrisen $A^(-1)$ finns, så är den unik.

Det finns flera sätt att hitta inversen av en matris, och vi ska titta på två av dem. På den här sidan kommer vi att överväga den adjoint matrismetoden, som anses vara standard i de flesta högre matematikkurser. Det andra sättet att hitta den inversa matrisen (metoden för elementära transformationer), som involverar användningen av Gauss-metoden eller Gauss-Jordan-metoden, behandlas i den andra delen.

Adjoint (union) matrismetod

Låt matrisen $A_(n\ gånger n)$ ges. För att hitta den inversa matrisen $A^(-1)$ krävs tre steg:

Hitta determinanten för matrisen $A$ och se till att $\Delta A\neq 0$, d.v.s. att matrisen A är icke degenererad.
Komponera algebraiska komplement $A_(ij)$ av varje element i matrisen $A$ och skriv ner matrisen $A_(n\ gånger n)^(*)=\left(A_(ij) \right)$ från den hittade algebraiska komplement.
Skriv den inversa matrisen med hänsyn till formeln $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Matrisen $(A^(*))^T$ hänvisas ofta till som den angränsande (ömsesidiga, allierade) matrisen för $A$.

Om beslutet tas manuellt, är den första metoden endast bra för matriser med relativt små beställningar: andra (), tredje (), fjärde (). För att hitta den inversa matrisen för en matris av högre ordning används andra metoder. Till exempel Gaussmetoden som diskuteras i andra delen.

Exempel #1

Hitta matris invers till matris $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Eftersom alla element i den fjärde kolumnen är lika med noll, då är $\Delta A=0$ (dvs matrisen $A$ är degenererad). Eftersom $\Delta A=0$ finns det ingen matris invers mot $A$.

Svar: matris $A^(-1)$ finns inte.

Exempel #2

Hitta matrisen invers till matrisen $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Kör en kontroll.

Vi använder adjoint matrismetoden. Låt oss först hitta determinanten för den givna matrisen $A$:

$$ \Delta A=\vänster| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Eftersom $\Delta A \neq 0$ existerar den inversa matrisen, så vi fortsätter lösningen. Hitta algebraiska komplement

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(aligned)

Komponera en matris av algebraiska tillägg: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transponera den resulterande matrisen: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (den resulterande matrisen kallas ofta adjoint eller unionsmatris till matrisen $A$). Med formeln $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, har vi:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

Så den inversa matrisen hittas: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \höger) $. För att kontrollera sanningen av resultatet räcker det att kontrollera sanningen av en av likheterna: $A^(-1)\cdot A=E$ eller $A\cdot A^(-1)=E$. Låt oss kontrollera likheten $A^(-1)\cdot A=E$. För att arbeta mindre med bråk, kommer vi att ersätta matrisen $A^(-1)$ inte i formen $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ men som $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \ end(array )\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( array)\right)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array )\right) =E $$

Svar: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Exempel #3

Hitta inversen av matrisen $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$. Kör en kontroll.

Låt oss börja med att beräkna determinanten för matrisen $A$. Så, determinanten för matrisen $A$ är:

$$ \Delta A=\vänster| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

Eftersom $\Delta A\neq 0$ existerar den inversa matrisen, så vi fortsätter lösningen. Vi hittar de algebraiska komplementen för varje element i den givna matrisen:

Vi komponerar en matris av algebraiska tillägg och transponerar den:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

Med formeln $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ får vi:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

Så $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. För att kontrollera sanningen av resultatet räcker det att kontrollera sanningen av en av likheterna: $A^(-1)\cdot A=E$ eller $A\cdot A^(-1)=E$. Låt oss kontrollera likheten $A\cdot A^(-1)=E$. För att arbeta mindre med bråk, kommer vi att ersätta matrisen $A^(-1)$ inte i formen $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, men som $\frac(1)(26)\ cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(array) \right) =\frac(1)(26)\cdot\left(\begin(array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (array) \right) =\left(\begin(array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

Kontrollen godkändes, den inversa matrisen $A^(-1)$ hittades korrekt.

Svar: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Exempel #4

Hitta matrisinvers av $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

För en matris av fjärde ordningen är det lite svårt att hitta den inversa matrisen med hjälp av algebraiska tillägg. Sådana exempel finns dock i kontrollarbetena.

För att hitta den inversa matrisen måste du först beräkna determinanten för matrisen $A$. Det bästa sättet att göra detta i den här situationen är att utöka determinanten i en rad (kolumn). Vi väljer valfri rad eller kolumn och hittar det algebraiska komplementet för varje element i den valda raden eller kolumnen.

Till exempel, för den första raden får vi:

$$ A_(11)=\left|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\left|\begin(array)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\left|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

Determinanten för matrisen $A$ beräknas med följande formel:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14) )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(justerad) $$

Algebraisk komplementmatris: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(array)\right)$.

Bifogad matris: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Invers matris:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Kontroll, om så önskas, kan göras på samma sätt som i de tidigare exemplen.

Svar: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(array) \right) $.

I den andra delen kommer ett annat sätt att hitta den inversa matrisen att övervägas, vilket innebär användning av transformationer av Gauss-metoden eller Gauss-Jordan-metoden.

ALGEBRAISKA TILLÄGG OCH MINOR

Låt oss ha en tredje ordningens determinant: .

Mindre motsvarande detta element aij tredje ordningens determinant kallas den andra ordningens determinant som erhålls från den givna genom att radera raden och kolumnen i vars skärningspunkt det givna elementet står, d.v.s. i-th rad och j-th kolumn. Minderåriga som motsvarar ett givet element aij vi kommer att beteckna M ij.

till exempel, mindre M12 motsvarande elementet en 12, kommer det att finnas en avgörande faktor 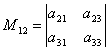, som erhålls genom att radera den första raden och den andra kolumnen från den givna determinanten.

Således visar formeln som bestämmer tredje ordningens determinant att denna determinant är lika med summan av produkterna av elementen i den första raden och deras motsvarande minor; medan moll motsvarar elementet en 12, tas med "–"-tecknet, dvs. kan skrivas det

(1)

På liknande sätt kan man införa definitioner av minderåriga för bestämningsfaktorer av andra ordningen och högre ordningen.

Låt oss presentera ytterligare ett koncept.

Algebraisk tillägg element aij determinant kallas dess minor M ij multiplicerat med (–1) i+j .

Algebraisk elementtillägg aij betecknas A ij.

Av definitionen får vi att sambandet mellan ett elements algebraiska komplement och dess underordnade uttrycks av likheten A ij= (–1) i+j M ij .

Till exempel,

Exempel. Givet en determinant. Att hitta A 13 , A 21 , A 32.

Det är lätt att se att med hjälp av algebraiska tillägg av element kan formel (1) skrivas som:

På samma sätt som denna formel kan man få nedbrytningen av determinanten över elementen i vilken rad eller kolumn som helst.

Till exempel kan sönderdelningen av determinanten över elementen i den andra raden erhållas enligt följande. Enligt egenskap 2 hos determinanten har vi:

Låt oss utöka den erhållna determinanten med elementen i den första raden.

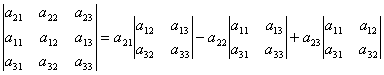(2)

Härifrån därför att andra ordningens determinanter i formel (2) är minorerna av elementen en 21, en 22, en 23. Alltså, d.v.s. vi har erhållit expansionen av determinanten med elementen i den andra raden.

På liknande sätt kan man få sönderdelningen av determinanten över elementen i den tredje raden. Med hjälp av egenskap 1 för determinanter (vid transponering) kan man visa att liknande expansioner också är giltiga för expansioner när det gäller kolumnelement.

Följande sats är alltså sann.

Sats (om expansion av determinanten i en given rad eller kolumn). Determinanten är lika med summan av produkterna av elementen i någon av dess rader (eller kolumner) och deras algebraiska komplement.

Allt ovanstående är sant för determinanter av vilken högre ordning som helst.

Exempel.

INVERS MATRIX

Konceptet med en invers matris introduceras endast för kvadratiska matriser.

Om en Aär alltså en kvadratisk matris omvänd för det är en matris en matris som betecknas A-1 och uppfyller villkoret. (Denna definition introduceras i analogi med multiplikationen av tal)