Vinogradovin matemaattinen tietosanakirja. Matemaattinen tietosanakirja. Vanhat ja uudet matematiikan luokitukset
Artikkelin sisältö
MATEMAA. Matematiikka määritellään yleensä luettelemalla joidenkin sen perinteisten alojen nimet. Ensinnäkin tämä on aritmetiikka, joka käsittelee lukujen tutkimusta, niiden välisiä suhteita ja numeroiden kanssa työskentelyn sääntöjä. Aritmetiikan tosiasiat ovat avoimia erilaisille konkreettisille tulkinnoille; esimerkiksi suhde 2 + 3 = 4 + 1 vastaa väitettä, että kaksi ja kolme kirjaa muodostavat yhtä monta kirjaa kuin neljä ja yksi. Mikä tahansa relaatio, kuten 2 + 3 = 4 + 1, ts. Puhtaasti matemaattisten objektien välistä suhdetta ilman viittausta mihinkään fyysisen maailman tulkintaan kutsutaan abstraktiksi. Matematiikan abstrakti luonne mahdollistaa sen käytön monenlaisten ongelmien ratkaisemisessa. Esimerkiksi algebra, joka käsittelee lukujen operaatioita, antaa sinun ratkaista ongelmia, jotka menevät aritmetiikkaa pidemmälle. Tarkempi matematiikan ala on geometria, jonka päätehtävänä on esineiden koon ja muodon tutkiminen. Algebrallisten menetelmien ja geometristen menetelmien yhdistäminen johtaa toisaalta trigonometriaan (alun perin omistettu geometristen kolmioiden tutkimukselle ja kattaa nyt paljon laajemman aihealueen) ja toisaalta analyyttiseen geometriaan, jossa geometrisia kappaleita ja kuvioita tutkitaan algebrallisin menetelmin. On olemassa useita korkeamman algebran ja geometrian haaroja, joilla on korkeampi abstraktioaste ja jotka eivät liity tavallisten lukujen ja tavallisten geometristen kuvioiden tutkimiseen; Geometristen tieteenalojen abstrakteimpia kutsutaan topologiaksi.
Matemaattinen analyysi käsittelee tilassa tai ajassa muuttuvien suureiden tutkimusta ja tukeutuu kahteen peruskäsitteeseen - funktioon ja rajaan, joita ei löydy matematiikan alkeellisista osioista. Aluksi matemaattinen analyysi koostui differentiaali- ja integraalilaskennasta, mutta nyt se sisältää muita osia.
Matematiikassa on kaksi pääaluetta - puhdas matematiikka, jossa painopiste on deduktiivisessa päättelyssä, ja sovellettu matematiikka. Termi "soveltava matematiikka" tarkoittaa joskus niitä matematiikan aloja, jotka on luotu nimenomaan tieteen tarpeita ja vaatimuksia tyydyttämään, ja joskus niitä eri tieteiden osia (fysiikka, taloustiede jne.), jotka käyttävät matematiikkaa ratkaisukeinona. heidän tehtävänsä. Monet yleiset väärinkäsitykset matematiikasta syntyvät näiden kahden "sovelletun matematiikan" tulkinnan välisestä sekaannuksesta. Aritmetiikka voi olla esimerkki soveltavasta matematiikasta ensimmäisessä merkityksessä ja kirjanpidosta toisessa mielessä.
Vastoin yleistä käsitystä, matematiikka kehittyy edelleen nopeasti. Mathematical Review julkaistaan vuosittain n. 8000 lyhyttä tiivistelmää artikkeleista, jotka sisältävät uusimmat tulokset - uusia matemaattisia faktoja, uusia todisteita vanhoista tosiseikoista ja jopa tietoa täysin uusista matematiikan alueista. Nykyinen suuntaus matematiikan opetuksessa on tuoda opiskelijat nykyaikaisiin, abstraktimpiin matemaattisiin ajatuksiin matematiikan opetuksen aikaisemmassa vaiheessa. Katso myös MATEMATIIKAN HISTORIA. Matematiikka on yksi sivilisaation kulmakivistä, mutta hyvin harvalla on käsitys tämän tieteen nykytilasta.
Matematiikka on kokenut valtavia muutoksia viimeisen sadan vuoden aikana sekä oppiaineissa että -menetelmissä. Tässä artikkelissa yritämme antaa yleiskuvan modernin matematiikan evoluution päävaiheista, joiden tärkeimpiä tuloksia voidaan pitää toisaalta puhtaan ja sovelletun matematiikan välisen kuilun kasvuna, ja toisaalta perinteisten matematiikan alueiden täydellinen uudelleenarviointi.
MATEMAATISEN MENETELMÄN KEHITTÄMINEN
Matematiikan synty.
Noin 2000 eaa havaittiin, että kolmiossa, jonka sivut ovat 3, 4 ja 5 pituusyksikköä, yksi kulmista on 90 ° (tämän havainnon ansiosta oli helppo rakentaa suora kulma käytännön tarpeisiin). Huomasitko silloin suhteen 5 2 = 3 2 + 4 2 ? Meillä ei ole tästä mitään tietoa. Muutama vuosisataa myöhemmin löydettiin yleinen sääntö: missä tahansa kolmiossa ABC suorassa kulmassa yläosassa A ja juhlia b = AC Ja c = AB, jonka väliin tämä kulma on suljettu, ja sitä vastakkainen puoli a = eKr suhde a 2 = b 2 + c 2. Voidaan sanoa, että tiede alkaa, kun yksittäisten havaintojen massa selitetään yhdellä yleisellä lailla; siksi "Pytagoraan lauseen" löytäminen voidaan nähdä yhtenä ensimmäisistä tunnetuista esimerkeistä todella tieteellisestä saavutuksesta.
Mutta vielä tärkeämpää tieteelle yleensä ja erityisesti matematiikan kannalta on se, että yleisen lain muotoilun ohella ilmaantuu yrityksiä sen todistamiseksi, ts. osoittavat, että se seuraa välttämättä muista geometrisista ominaisuuksista. Yksi itämaisista "todistuksista" on yksinkertaisuudessaan erityisen graafinen: neliöön on kaiverrettu neljä kolmiota, jotka ovat yhtä suuret kuin annettu. BCDE kuten piirustuksessa näkyy. neliön alue a 2 on jaettu neljään yhtä suureen kolmioon, joiden kokonaispinta-ala on 2 eaa ja neliö AFGH alue ( b – c) 2. Tällä tavoin, a 2 = (b – c) 2 + 2eaa = (b 2 + c 2 – 2eaa) + 2eaa = b 2 + c 2. On opettavaista mennä askel pidemmälle ja selvittää tarkemmin, mitkä "aikaisemmat" ominaisuudet oletetaan tiedossa. Ilmeisin tosiasia on, että kolmioiden jälkeen BAC Ja BEF tarkasti, ilman rakoja ja päällekkäisyyksiä, "sovitettu" sivuille BA Ja bf, mikä tarkoittaa, että kaksi kulmaa kärjessä B Ja FROM kolmiossa ABS yhdessä muodostavat 90° kulman ja siksi sen kaikkien kolmen kulman summa on 90° + 90° = 180°. Yllä oleva "todistus" käyttää myös kaavaa ( eaa/2) kolmion pinta-alalle ABC 90° kulmassa yläreunassa A. Itse asiassa käytettiin myös muita oletuksia, mutta sanottu riittää, jotta voimme selvästi nähdä matemaattisen todistuksen olennaisen mekanismin - deduktiivisen päättelyn, joka mahdollistaa puhtaasti loogisten argumenttien käytön (perustuu esimerkissämme oikein valmistettuun materiaaliin - halkaisu). neliö) päätellä tunnetuista tuloksista uusia ominaisuuksia, jotka eivät yleensä seuraa suoraan saatavilla olevista tiedoista.
Aksioomat ja todistusmenetelmät.
Yksi matemaattisen menetelmän peruspiirteistä on prosessi, jossa luodaan huolellisesti rakennettujen puhtaasti loogisten argumenttien avulla lauseketju, jossa jokainen peräkkäinen linkki liittyy edellisiin. Ensimmäinen melko ilmeinen huomio on, että jokaisella ketjulla on oltava ensimmäinen lenkki. Tämä seikka tuli kreikkalaisille ilmeiseksi, kun he alkoivat systematisoida matemaattisten argumenttien koodia 7. vuosisadalla. eKr. Kreikkalaisilta kesti n. 200 vuotta vanhoja, ja säilyneet asiakirjat antavat vain karkean kuvan siitä, kuinka he tarkalleen toimivat. Meillä on tarkkoja tietoja vain tutkimuksen lopputuloksesta - kuuluisasta Alkuja Eukleides (noin 300 eKr.). Eukleides aloittaa luettelemalla alkuasemat, joista kaikki loput johdetaan puhtaasti loogisella tavalla. Näitä määräyksiä kutsutaan aksioomeiksi tai postulaatteiksi (termit ovat käytännössä vaihdettavissa keskenään); ne ilmaisevat joko hyvin yleisiä ja jokseenkin epämääräisiä kaikenlaisten esineiden ominaisuuksia, kuten "kokonaisuus on suurempi kuin osa", tai joitain erityisiä matemaattisia ominaisuuksia, kuten sitä, että mitä tahansa kahta pistettä varten on yksi suora viiva, joka yhdistää ne . Meillä ei myöskään ole tietoa siitä, pitivätkö kreikkalaiset aksioomien "totuutta" syvempää merkitystä, vaikka on joitakin vihjeitä siitä, että kreikkalaiset keskustelivat niistä jonkin aikaa ennen tiettyjen aksioomien hyväksymistä. Euklideissa ja hänen seuraajissaan aksioomit esitetään vain lähtökohtina matematiikan rakentamiselle ilman, että niiden luonnetta kommentoida.
Mitä tulee todistusmenetelmiin, ne pääsääntöisesti pelkistettiin aiemmin todistettujen lauseiden suoraan käyttöön. Joskus päättelyn logiikka osoittautui kuitenkin monimutkaisemmaksi. Mainitsemme tässä Eukleideen suosikkimenetelmän, josta on tullut osa matematiikan jokapäiväistä käytäntöä - epäsuora todistus eli ristiriitatodistus. Alkuperäisenä esimerkkinä ristiriitaisesta todistuksesta näytämme, että shakkilautaa, josta on leikattu kaksi kulmakenttää, jotka sijaitsevat diagonaalin vastakkaisissa päissä, ei voida peittää dominoilla, joista jokainen on yhtä suuri kuin kaksi kenttää. (Oletetaan, että kukin shakkilaudan ruutu tulee peittää vain kerran.) Oletetaan, että päinvastainen ("vastakohta") väite on tosi, ts. että lauta voidaan peittää dominoilla. Jokainen laatta peittää yhden mustan ja yhden valkoisen neliön, joten riippumatta siitä, mihin dominot sijoitetaan, ne peittävät yhtä monta mustaa ja valkoista ruutua. Kuitenkin, koska kaksi kulmaruutua on poistettu, shakkilaudalla (jossa alun perin oli yhtä monta mustaa ruutua kuin valkoisia) on kaksi yhden väristä ruutua enemmän kuin toisen värisiä ruutuja. Tämä tarkoittaa, että alkuperäinen oletuksemme ei voi olla totta, koska se johtaa ristiriitaan. Ja koska ristiriitaiset väitteet eivät voi olla molempia vääriä samanaikaisesti (jos toinen niistä on epätosi, niin päinvastoin on totta), alkuperäisen oletuksemme on oltava tosi, koska ristiriitainen olettamus on väärä; siksi shakkilautaa, jossa on kaksi leikattua kulmaruutua, jotka on sijoitettu vinottain, ei voida peittää dominolla. Joten todistaaksemme tietyn väitteen voimme olettaa, että se on väärä, ja päätellä tästä oletuksesta ristiriidan jonkin muun väitteen kanssa, jonka totuus on tiedossa.
Erinomainen esimerkki ristiriitaisesta todistamisesta, josta tuli yksi antiikin Kreikan matematiikan kehityksen virstanpylväitä, on todiste, joka ei ole rationaalinen luku, ts. ei ole esitettävissä murto-osana p/q, missä p Ja q- kokonaislukuja. Jos , niin 2 = p 2 /q 2, mistä p 2 = 2q 2. Oletetaan, että kokonaislukuja on kaksi p Ja q, mille p 2 = 2q 2. Toisin sanoen oletetaan, että on olemassa kokonaisluku, jonka neliö on kaksi kertaa toisen kokonaisluvun neliö. Jos jokin kokonaisluku täyttää tämän ehdon, yhden niistä on oltava pienempi kuin kaikki muut. Keskitytään pienimpään näistä luvuista. Olkoon se numero p. Vuodesta 2 q 2 on parillinen luku ja p 2 = 2q 2, sitten numero p 2:n on oltava parillinen. Koska kaikkien parittomien lukujen neliöt ovat parittomia, ja neliö p 2 on parillinen, joten itse luku p täytyy olla tasainen. Toisin sanoen numero p kaksi kertaa jokin kokonaisluku r. Koska p = 2r Ja p 2 = 2q 2, meillä on: (2 r) 2 = 4r 2 = 2q 2 ja q 2 = 2r 2. Viimeisellä tasa-arvolla on sama muoto kuin tasa-arvolla p 2 = 2q 2 , ja voimme toistaen samaa päättelyä osoittaa, että numero q on parillinen ja että on olemassa sellainen kokonaisluku s, mitä q = 2s. Mutta toisaalta q 2 = (2s) 2 = 4s 2 ja siitä lähtien q 2 = 2r 2, päättelemme, että 4 s 2 = 2r 2 tai r 2 = 2s 2. Joten saamme toisen kokonaisluvun, joka täyttää ehdon, että sen neliö on kaksi kertaa toisen kokonaisluvun neliö. Mutta toisaalta p ei voi olla pienin tällainen luku (kos r = p/2), vaikka alun perin oletimme, että se on pienin sellaisista luvuista. Siksi alkuperäinen oletuksemme on väärä, koska se johtaa ristiriitaan, ja siksi tällaisia kokonaislukuja ei ole olemassa p Ja q, mille p 2 = 2q 2 (eli sellainen, että ). Ja tämä tarkoittaa, että luku ei voi olla järkevä.
Euklideista 1800-luvun alkuun.
Tänä aikana matematiikka on muuttunut merkittävästi kolmen innovaation seurauksena.
(1) Algebran kehityksen aikana keksittiin symbolinen merkintämenetelmä, joka mahdollisti yhä monimutkaisempien määrien välisten suhteiden esittämisen lyhennetyssä muodossa. Esimerkkinä vaivasta, joka syntyisi, jos tällaista "kursiivista kirjoitusta" ei olisi olemassa, yritetään välittää sanoin suhde ( a + b) 2 = a 2 + 2ab + b 2: "Neliön pinta-ala, jonka sivu on yhtä suuri kuin kahden annetun neliön sivujen summa, on yhtä suuri kuin niiden pinta-alojen summa sekä kaksi kertaa sellaisen suorakulmion pinta-ala, jonka sivut ovat yhtä suuret annetut neliöt."
(2) Luominen 1600-luvun ensimmäisellä puoliskolla. analyyttinen geometria, joka mahdollisti klassisen geometrian ongelman pelkistämisen johonkin algebralliseen ongelmaan.
(3) Infinitesimaalilaskennan luominen ja kehittäminen vuosien 1600 ja 1800 välillä, mikä mahdollisti helposti ja systemaattisesti satoja rajan ja jatkuvuuden käsitteisiin liittyviä ongelmia, joista vain harvat ratkaistiin hyvin vaivoin muinaisen Kreikan toimesta. matemaatikot. Näitä matematiikan aloja käsitellään tarkemmin artikkeleissa ALGEBRA; ANALYYTTINEN GEOMETRIA ; MATEMAATTINEN ANALYYSI ; GEOMETRIAN KATSAUS.
Alkaen 1700-luvulta. vähitellen selvittää kysymyksen, joka on tähän asti jäänyt ratkaisematta. Mitä on matematiikka? Ennen vuotta 1800 vastaus oli riittävän yksinkertainen. Tuohon aikaan eri tieteiden välillä ei ollut selkeitä rajoja, matematiikka oli osa "luonnonfilosofiaa" - systemaattista luonnon tutkimista renessanssin ja 1600-luvun alun suurten uudistajien ehdottamilla menetelmillä. - Galileo (1564–1642), F. Bacon (1561–1626) ja R. Descartes (1596–1650). Uskottiin, että matemaatikoilla oli oma tutkimusalue - numerot ja geometriset esineet, ja että matemaatikot eivät käyttäneet kokeellista menetelmää. Newton ja hänen seuraajansa opiskelivat kuitenkin mekaniikkaa ja tähtitiedettä aksiomaattisella menetelmällä, samalla tavalla kuin Euklidesin geometria esitettiin. Yleisemmin tunnustettiin, että mistä tahansa tieteestä, jossa kokeen tulokset voidaan esittää käyttämällä numeroita tai lukujärjestelmiä, tulee matematiikan sovellusalue (fysiikassa tämä ajatus perustettiin vasta 1800-luvulla).
Matemaattisesti käsiteltyjä kokeellisen tieteen aloja kutsutaan usein "soveltavaksi matematiikaksi"; Tämä on erittäin valitettava nimi, koska näissä sovelluksissa ei ole klassisten tai nykyaikaisten standardien mukaan (tiukkassa merkityksessä) todella matemaattisia argumentteja, koska ei-matemaattiset objektit ovat niissä tutkimuksen kohteena. Kun kokeelliset tiedot on käännetty lukujen tai yhtälöiden kielelle (sellainen "käännös" vaatii usein suurta kekseliäisyyttä "soveltavan" matemaatikon puolelta), ilmaantuu mahdollisuus matemaattisten lauseiden laajaan soveltamiseen; tulos käännetään sitten takaisin ja sitä verrataan havaintoihin. Se tosiasia, että termiä "matematiikka" käytetään tällaiseen prosessiin, on yksi loputtomien väärinkäsitysten lähteistä. "Klassisena" aikana, josta nyt puhumme, tällaista väärinkäsitystä ei ollut olemassa, koska samat ihmiset olivat sekä "soveltuvia" että "puhtaita" matemaatikoita, jotka käsittelivät samanaikaisesti matemaattisen analyysin tai lukuteorian ongelmia ja ongelmia. dynamiikasta tai optiikasta. Lisääntynyt erikoistuminen ja taipumus erottaa "puhtaat" ja "soveltuvat" matemaatikot kuitenkin heikensivät merkittävästi aiemmin olemassa olevaa universaalisuuden perinnettä, ja tiedemiehet, jotka J. von Neumannin (1903–1957) tavoin pystyivät harjoittamaan aktiivista tieteellistä toimintaa sekä sovellettuina ja puhtaassa matematiikassa on tullut pikemminkin poikkeus kuin sääntö.
Millainen on matemaattisten objektien luonne - numerot, pisteet, viivat, kulmat, pinnat jne., joiden olemassaoloa pidimme itsestäänselvyytenä? Mitä "totuuden" käsite tarkoittaa suhteessa tällaisiin esineisiin? Klassisella aikakaudella näihin kysymyksiin annettiin varsin selvät vastaukset. Tietenkin tuon aikakauden tiedemiehet ymmärsivät selvästi, että aistimiemme maailmassa ei ole sellaisia asioita kuin Eukleideen "lopetta pidennetty suora viiva" tai "piste ilman mittoja", kuten ei ole "puhtaita metalleja", "yksikromaattista valoa". ", "lämpöeristetyt järjestelmät" jne. .d., joita kokeilijat käyttävät perusteluissaan. Kaikki nämä käsitteet ovat "platonisia ideoita", ts. eräänlaisia generatiivisia empiiristen käsitteiden malleja, vaikkakin luonteeltaan radikaalisti erilaisia. Siitä huolimatta oletettiin hiljaisesti, että ideoiden fyysiset "kuvat" voisivat olla mielivaltaisen lähellä itse ideoita. Siinä määrin kuin mitä tahansa voidaan sanoa esineiden läheisyydestä ideoihin, "ideoiden" sanotaan olevan fyysisten objektien niin sanotusti "rajatapauksia". Tästä näkökulmasta katsottuna Eukleideen aksioomit ja niistä johdetut lauseet ilmaisevat "ideaalien" objektien ominaisuuksia, joiden on vastattava ennustettavia kokeellisia tosiasioita. Esimerkiksi kolmen avaruuden pisteen muodostaman kolmion kulmien mittaamisen optisilla menetelmillä "ihanteellisessa tapauksessa" tulisi antaa summa, joka on 180 °. Toisin sanoen aksioomit asetetaan samalle tasolle fyysisten lakien kanssa, ja siksi niiden "totuus" havaitaan samalla tavalla kuin fyysisten lakien totuus; nuo. aksioomien loogiset seuraukset tarkistetaan vertaamalla niitä kokeellisiin tietoihin. Tietysti yksimielisyys voidaan saavuttaa vain sen virheen rajoissa, joka liittyy sekä mittauslaitteen "epätäydelliseen" luonteeseen kuin mitattavan kohteen "epätäydelliseen luonteeseen". Aina kuitenkin oletetaan, että jos lait ovat "tosia", niin mittausprosessien parannukset voivat periaatteessa tehdä mittausvirheestä niin pienen kuin halutaan.
Koko 1700-luvun oli yhä enemmän todisteita siitä, että kaikki perusaksioomista johdetut seuraukset, erityisesti tähtitieteen ja mekaniikassa, ovat yhdenmukaisia kokeellisten tietojen kanssa. Ja koska nämä seuraukset saatiin käyttämällä tuolloin olemassa olevaa matemaattista laitteistoa, saavutetut menestykset vahvistivat käsitystä Eukleideen aksioomien totuudesta, joka, kuten Platon sanoi, "on selvä kaikille" ja josta ei keskustella.
Epäilyjä ja uusia toiveita.
Ei-euklidinen geometria.
Eukleideen esittämistä postulaattien joukosta yksi oli niin epäselvä, että jopa suuren matemaatikon ensimmäiset oppilaat pitivät sitä järjestelmän heikkona kohdanna. Alkoi. Kyseinen aksiooma väittää, että tietyn suoran ulkopuolella olevan pisteen kautta voidaan piirtää vain yksi suora yhdensuuntainen annetun suoran kanssa. Useimmat geometrit uskoivat, että rinnakkaisaksiooma voidaan todistaa käyttämällä muita aksioomeja, ja että Eukleides muotoili väitteen rinnakkaisuudesta postulaatiksi yksinkertaisesti siksi, että hän ei pystynyt keksimään sellaista todistetta. Mutta vaikka parhaat matemaatikot yrittivät ratkaista rinnakkaisongelman, kukaan heistä ei onnistunut ohittamaan Eukleideen. Lopulta 1700-luvun jälkipuoliskolla. Eukleideen yhtäläisyyden postulaattia yritettiin todistaa ristiriitaisesti. On ehdotettu, että rinnakkainen aksiooma on väärä. A priori Eukleideen postulaatti voi osoittautua vääräksi kahdessa tapauksessa: jos on mahdotonta piirtää yhtä yhdensuuntaista suoraa annetun suoran ulkopuolisen pisteen läpi; tai jos sen läpi voidaan vetää useita yhdensuuntaisia viivoja. Kävi ilmi, että muut aksioomit sulkevat pois ensimmäisen a priori mahdollisuuden. Otettuaan käyttöön uuden aksiooman perinteisen rinnakkaisaksiooman sijaan (että tietyn suoran ulkopuolisen pisteen kautta voidaan vetää useita samansuuntaisia suoria) matemaatikot yrittivät johtaa siitä väitteen, joka oli ristiriidassa muiden aksioomien kanssa, mutta epäonnistui: vaikka kuinka paljon he yrittivät poimia seurauksia uudesta "anti-euklidisesta" tai "ei-euklidisesta" aksioomasta, ristiriitaa ei ilmennyt. Lopulta NI Lobatševski (1793–1856) ja J. Bolyai (1802–1860) ymmärsivät toisistaan riippumatta, että Euklidesin postulaatti rinnakkaisista on mahdoton todistaa, eli toisin sanoen, ristiriitaa ei ilmene "ei-euklidisessa geometriassa". .
Ei-euklidisen geometrian tultua esiin useita filosofisia ongelmia syntyi välittömästi. Koska väite aksioomien a priori välttämättömyydestä katosi, ainoa tapa testata niiden "totuutta" jäi - kokeellisesti. Mutta kuten A. Poincaré (1854–1912) myöhemmin huomautti, minkä tahansa ilmiön kuvauksessa on piilotettu niin monia fyysisiä olettamuksia, että mikään koe ei voi tarjota vakuuttavaa näyttöä matemaattisen aksiooman totuudesta tai virheellisyydestä. Lisäksi, vaikka olettaisimme, että maailmamme on "ei-euklidinen", seuraako siitä, että kaikki euklidinen geometria on väärä? Sikäli kuin tiedetään, kukaan matemaatikko ei ole koskaan harkinnut tällaista olettamusta vakavasti. Intuitio ehdotti, että sekä euklidiset että ei-euklidiset geometriat ovat esimerkkejä täysimittaisesta matematiikasta.
Matemaattiset hirviöt.
Yllättäen samat johtopäätökset tulivat täysin eri suunnasta - löydettiin esineitä, jotka syöksyivät 1800-luvun matemaatikot. järkyttynyt ja nimitetty "matematiikan hirviöiksi". Tämä löytö liittyy suoraan matemaattisen analyysin erittäin hienovaraisiin kysymyksiin, jotka nousivat esiin vasta 1800-luvun puolivälissä. Vaikeuksia syntyi, kun yritettiin löytää tarkkaa matemaattista analogia kokeelliselle käyrän käsitteelle. "Jatkuvan liikkeen" käsitteen ydin (esimerkiksi piirustuskynän kärki liikkuu paperiarkin poikki) oli tarkan matemaattisen määritelmän kohteena, ja tämä tavoite saavutettiin, kun jatkuvuuden käsite sai tiukan matemaattisen merkitys ( cm. myös KÄYRÄ). Intuitiivisesti vaikutti siltä, että "käyrällä" jokaisessa pisteessään oli ikään kuin suunta, ts. yleensä jokaisen pisteensä läheisyydessä käyrä käyttäytyy lähes samalla tavalla kuin suora. (Toisaalta on helppo kuvitella, että käyrällä on äärellinen määrä kulmapisteitä, "kierteitä", kuten monikulmiossa.) Tämä vaatimus voitaisiin muotoilla matemaattisesti, nimittäin käyrän tangentin olemassaolo oletettiin. , ja 1800-luvun puoliväliin asti. uskottiin, että "käyrällä" oli tangentti melkein kaikissa pisteissään, ehkä joitakin "erikoispisteitä" lukuun ottamatta. Siksi "käyrien" löytäminen, joilla ei ollut tangenttia missään vaiheessa, aiheutti todellisen skandaalin ( cm. myös FUNKTIOTEORIA). (Trigonometriaan ja analyyttiseen geometriaan perehtynyt lukija voi helposti varmistaa, että yhtälön antama käyrä y = x synti(1/ x), sillä ei ole tangenttia origossa, mutta käyrän määrittäminen, jolla ei ole tangenttia missään pisteessä, on paljon vaikeampaa.)
Hieman myöhemmin saatiin paljon "patologisempi" tulos: oli mahdollista rakentaa esimerkki käyrästä, joka täyttää neliön kokonaan. Sittemmin on keksitty satoja tällaisia "hirviöitä" vastoin "tervettä järkeä". On korostettava, että tällaisten epätavallisten matemaattisten objektien olemassaolo seuraa perusaksioomista yhtä tiukasti ja loogisesti virheettömästi kuin kolmion tai ellipsin olemassaolo. Koska matemaattiset "hirviöt" eivät voi vastata mitään kokeellista kohdetta, ja ainoa mahdollinen johtopäätös on, että matemaattisten "ideoiden" maailma on paljon rikkaampi ja epätavallisempi kuin voisi odottaa, ja vain harvoilla niistä on vastaavuuksia aistimiemme maailmassa. . Mutta jos matemaattiset "hirviöt" seuraavat loogisesti aksioomista, voidaanko aksioomia silti pitää totta?
Uusia esineitä.
Yllä olevat tulokset vahvistuivat toiselta puolelta: matematiikassa, pääasiassa algebrassa, alkoi ilmaantua peräkkäin uusia matemaattisia objekteja, jotka olivat lukukäsitteen yleistyksiä. Tavalliset kokonaisluvut ovat melko "intuitiivisia" eikä ole ollenkaan vaikeaa päästä kokeelliseen murto-käsitteeseen (vaikka täytyy myöntää, että yksikön jakaminen useisiin yhtäläisiin osiin ja niistä useiden valitseminen on luonnostaan erilaista kuin prosessi laskemisesta). Sen jälkeen kun kävi selväksi, että lukua ei voida esittää murtolukuna, kreikkalaiset joutuivat harkitsemaan irrationaalisia lukuja, joiden oikea määritelmä rationaalisten lukujen likiarvojen äärettömällä sarjalla kuuluu ihmismielen korkeimpiin saavutuksiin, mutta tuskin vastaa mitään todellista fyysisessä maailmassamme (jossa mikä tahansa mittaus on aina alttiina virheille). Siitä huolimatta irrationaalisten lukujen käyttöönotto tapahtui enemmän tai vähemmän fyysisten käsitteiden "idealisoinnin" hengessä. Mutta entä negatiiviset luvut, jotka pikkuhiljaa suuren vastustuksen jälkeen alkoivat tulla tieteelliseen käyttöön algebran kehityksen yhteydessä? Voidaan täysin varmuudella todeta, ettei ollut olemassa valmiita fyysisiä objekteja, joista alkaen voisimme kehittää negatiivisen luvun käsitettä suoran abstraktion prosessilla, ja alkebran kurssin opetuksessa on esitettävä monia apu- ja melko monimutkaisia esimerkkejä (suuntautuneet segmentit, lämpötilat, velat jne.) selittämään, mitä negatiiviset luvut ovat. Tämä kanta on hyvin kaukana "selkeästä kaikille", kuten Platon vaati matematiikan taustalla olevilta ideoilta, ja ei ole harvinaista tavata korkeakoulututkinnon suorittaneita, joille merkkisääntö on edelleen mysteeri (- a)(–b) = ab. Katso myös NUMERO .
Tilanne on vielä pahempi "kuvitteellisilla" tai "kompleksisilla" numeroilla, koska ne sisältävät "luvun" i, sellasta i 2 = -1, mikä on selkeä merkkisäännön vastainen. Siitä huolimatta matemaatikot 1500-luvun lopusta. älä epäröi suorittaa laskelmia kompleksiluvuilla ikään kuin ne olisivat "järkeviä", vaikka 200 vuotta sitten he eivät voineet määritellä näitä "objekteja" tai tulkita niitä millään apukonstruktiolla, koska esimerkiksi ne tulkittiin käyttämällä suunnattuja segmenttejä negatiivisia lukuja . (Vuoden 1800 jälkeen kompleksiluvuille ehdotettiin useita tulkintoja, joista tunnetuin on vektorien avulla tasossa.)
moderni aksiomatiikka.
Vallankumous tapahtui 1800-luvun jälkipuoliskolla. Ja vaikka siihen ei liittynyt virallisten lausuntojen hyväksymistä, todellisuudessa kyse oli eräänlaisen "itsenäisyysjulistuksen" julistamisesta. Tarkemmin sanottuna julistuksesta de facto matematiikan riippumattomuudesta ulkomaailmasta.
Tästä näkökulmasta katsottuna matemaattiset "objektit", jos niiden "olemassaolosta" ylipäätään on järkevää puhua, ovat puhtaita mielen luomuksia, ja onko niillä mitään "vastaavuutta" ja sallivatko ne "tulkinnat" fyysinen maailma, sillä matematiikalla ei ole merkitystä (vaikka itse kysymys on mielenkiintoinen).
"Todet" lausunnot sellaisista "objekteista" ovat kaikki samoja loogisia seurauksia aksioomista. Mutta nyt aksioomia on pidettävä täysin mielivaltaisina, ja siksi niiden ei tarvitse olla "ilmeisiä" tai pääteltävissä jokapäiväisestä kokemuksesta "idealisoinnin" avulla. Käytännössä täydellistä vapautta rajoittavat erilaiset näkökohdat. Tietenkin "klassiset" objektit ja niiden aksioomit pysyvät ennallaan, mutta nyt niitä ei voida pitää matematiikan ainina esineinä ja aksioomeina, ja tapana heittää pois tai muokata aksioomia niin, että niitä on mahdollista käyttää eri tavoin, kuten tehtiin siirtyessä euklidisesta geometriasta ei-euklidiseen geometriaan. (Näin saatiin lukuisia muunnelmia "ei-euklidisista" geometrioista kuin euklidisesta geometriasta ja Lobatševski-Bolyai-geometriasta; on esimerkiksi ei-euklidisia geometrioita, joissa ei ole yhdensuuntaisia viivoja.)
Haluaisin korostaa yhtä seikkaa, joka seuraa matemaattisten "objektien" uudesta lähestymistavasta: kaikkien todisteiden tulee perustua yksinomaan aksioomiin. Jos muistamme matemaattisen todisteen määritelmän, tällainen lausunto voi tuntua toistolta. Klassisessa matematiikassa tätä sääntöä noudatettiin kuitenkin harvoin sen esineiden tai aksioomien "intuitiivisen" luonteen vuoksi. Jopa Alkuja Eukleides kaikesta näennäisestä "tiukkuudestaan" huolimatta monia aksioomia ei ole muotoiltu eksplisiittisesti ja monet ominaisuudet joko oletetaan tai otetaan käyttöön ilman riittävää perustetta. Jotta euklidinen geometria voitaisiin asettaa vankalle perustalle, sen periaatteet tarvittiin kriittisesti. Sanomattakin on selvää, että todisteen pienimpien yksityiskohtien pedanttinen hallinta on seurausta "hirviöiden" ilmestymisestä, jotka ovat opettaneet nykyajan matemaatikot olemaan varovaisia johtopäätöksissään. Kaikkein vaarattomin ja "itsestään ilmeisin" väite klassisista esineistä, kuten väite, että käyrä, joka yhdistää pisteitä, jotka sijaitsevat suoran vastakkaisilla puolilla, leikkaa välttämättä tämän suoran, modernissa matematiikassa vaatii tiukan muodollisen todisteen.
Saattaa tuntua paradoksaalliselta sanoa, että juuri sen aksioomien noudattamisen vuoksi moderni matematiikka toimii selkeänä esimerkkinä siitä, mitä minkä tahansa tieteen tulee olla. Tästä huolimatta tämä lähestymistapa havainnollistaa erästä tieteellisen ajattelun perustavanlaatuisimmista prosesseista ominaista piirrettä - tarkan tiedon saamista puutteellisen tiedon tilanteessa. Tietyn esineluokan tieteellinen tutkimus viittaa siihen, että ne ominaisuudet, jotka mahdollistavat kohteen erottamisen toisesta, unohdetaan tarkoituksella ja säilytetään vain tarkasteltavien esineiden yleiset piirteet. Se, mikä erottaa matematiikan yleisestä tieteiden kirjosta, on tämän ohjelman tiukka noudattaminen sen kaikissa kohdissa. Uskotaan, että matemaattiset objektit määräytyvät täysin näiden objektien teoriassa käytettyjen aksioomien avulla; tai, Poincarén sanoin, aksioomit toimivat kohteiden "naamioituneina määritelminä", joihin ne viittaavat.
MODERNI MATEMATIIKKA
Vaikka minkä tahansa aksioomien olemassaolo on teoriassa mahdollista, vain pieni määrä aksioomia on ehdotettu ja tutkittu tähän mennessä. Yleensä yhtä tai useampaa teoriaa kehitettäessä havaitaan, että joitain todistusjärjestelmiä toistetaan enemmän tai vähemmän samanlaisissa olosuhteissa. Kun yleisissä todisteiden kaavioissa käytetyt ominaisuudet on löydetty, ne muotoillaan aksioomien muotoon ja niiden seuraukset rakennetaan yleiseksi teoriaksi, joka ei liity suoraan niihin erityisiin konteksteihin, joista aksioomit on abstraktoitu. Näin saadut yleiset lauseet soveltuvat kaikkiin matemaattisiin tilanteisiin, joissa on objektijärjestelmiä, jotka täyttävät vastaavat aksioomit. Samojen todistusjärjestelmien toistaminen eri matemaattisissa tilanteissa osoittaa, että kyseessä on saman yleisen teorian erilaisia konkretisointeja. Tämä tarkoittaa, että sopivan tulkinnan jälkeen tämän teorian aksioomista tulee teoreemoja joka tilanteessa. Mikä tahansa aksioomista päätelty ominaisuus pätee kaikissa näissä tilanteissa, mutta jokaiselle tapaukselle ei tarvita erillistä todistetta. Tällaisissa tapauksissa matemaattisilla tilanteilla sanotaan olevan sama matemaattinen "rakenne".
Käytämme rakenteen käsitettä jokapäiväisessä elämässämme. Jos lämpömittari näyttää 10°C ja ennustetoimisto ennustaa lämpötilan nousua 5°C, odotamme ilman laskelmia 15°C. Jos kirja avataan sivulle 10 ja meitä pyydetään katsomaan 5 sivua pidemmälle, emme epäröi avata sitä 15. sivulla, välisivuja laskematta. Molemmissa tapauksissa uskomme, että numeroiden lisääminen antaa oikean tuloksen niiden tulkinnasta riippumatta - lämpötilan tai sivunumeroiden muodossa. Meidän ei tarvitse opetella yhtä aritmetiikkaa lämpömittareille ja toista sivunumeroille (vaikka käytämme kelloille erityistä aritmetiikkaa, jossa 8 + 5 = 1, koska kelloilla on erilainen rakenne kuin kirjan sivuilla). Matemaatikoille kiinnostaville rakenteille on ominaista hieman korkeampi monimutkaisuus, mikä on helppo nähdä esimerkeistä, joiden analyysi on omistettu tämän artikkelin kahdelle seuraavalle osalle. Yksi niistä käsittelee ryhmien teoriaa sekä matemaattisia rakenteita ja isomorfismeja.
Ryhmäteoria.
Ymmärtääksemme paremmin edellä hahmoteltua prosessia, meidän on otettava vapaus tarkastella nykyaikaisen matemaatikon laboratoriossa ja tarkastella lähemmin yhtä hänen päätyökaluaan - ryhmäteoriaa ( cm. myös ALGEBRAN TIIVISTELMÄ). Ryhmä on objektien kokoelma (tai "joukko"). G, jolle määritellään toiminto, joka yhdistää mitkä tahansa kaksi objektia tai elementtiä a, b alkaen G, otettu määritetyssä järjestyksessä (ensimmäinen on elementti a, toinen on elementti b), kolmas elementti c alkaen G tiukasti määritellyn säännön mukaan. Lyhytyyden vuoksi merkitsemme tätä elementtiä a*b; tähti (*) tarkoittaa kahden elementin koostumuksen toimintaa. Tämän toiminnon, jota kutsumme ryhmäkertolaskuksi, on täytettävä seuraavat ehdot:
(1) mille tahansa kolmelle elementille a, b, c alkaen G assosiaatioominaisuus täyttyy: a* (b*c) = (a*b) *c;
(2) sisään G sellainen elementti on olemassa e, joka mille tahansa elementille a alkaen G on suhde e*a = a*e = a; tämä elementti e kutsutaan ryhmän identiteetiksi tai neutraaliksi elementiksi;
(3) mille tahansa elementille a alkaen G sellainen elementti on olemassa a¢, jota kutsutaan käänteiseksi tai symmetriseksi elementtiin a, mitä a*aў = aў* a = e.
Jos nämä ominaisuudet otetaan aksioomeina, niin niiden loogiset seuraukset (muista aksioomeista tai lauseista riippumatta) muodostavat yhdessä sen, mitä yleisesti kutsutaan ryhmäteoriaksi. Näiden johtopäätösten päättäminen lopullisesti osoittautui erittäin hyödylliseksi, koska ryhmiä käytetään laajalti kaikilla matematiikan aloilla. Tuhansista mahdollisista ryhmäesimerkeistä valitsemme vain muutaman yksinkertaisimman.
(a) Murtoluvut p/q, missä p Ja q ovat mielivaltaisia kokonaislukuja i1 (for q= 1 saamme tavallisia kokonaislukuja). Murtoluvut p/q muodostaa ryhmän suhteessa ryhmän kertolaskuun ( p/q) *(r/s) = (PR)/(qs). Ominaisuudet (1), (2), (3) johtuvat aritmeettisen aksioomista. Todella, [( p/q) *(r/s)] *(t/u) = (prt)/(qsu) = (p/q)*[(r/s)*(t/u)]. Identiteettielementti on numero 1 = 1/1, koska (1/1)*( p/q) = (1H p)/(1H q) = p/q. Lopuksi alkio käänteinen murtoluvulle p/q, on murto-osa q/p, koska ( p/q)*(q/p) = (pq)/(pq) = 1.
(b) Tarkastellaan G neljän kokonaisluvun joukko 0, 1, 2, 3 ja as a*b- divisioonan loppuosa a + b 4. Näin esitellyn toimenpiteen tulokset on esitetty taulukossa. 1 (elementti a*b seisoo linjan risteyksessä a ja sarake b). On helppo tarkistaa, että ominaisuudet (1)–(3) täyttyvät ja numero 0 on identiteettielementti.
(c) Valitsemme kuten G joukko numeroita 1, 2, 3, 4 ja as a*b- divisioonan loppuosa ab(tavallinen tuote) 5:llä. Tuloksena saamme taulukon. 2. On helppo tarkistaa, että ominaisuudet (1)–(3) täyttyvät ja 1 on identiteettielementti.
(d) Neljä objektia, kuten neljä numeroa 1, 2, 3, 4, voidaan järjestää riviin 24 eri tavalla. Jokainen sijainti voidaan visualisoida muunnoksena, joka muuttaa "luonnollisen" sijainnin tietyksi; esimerkiksi sijainti 4, 1, 2, 3 saadaan muunnoksen tuloksena
S: 1 ® 4, 2 ® 1, 3 ® 2, 4 ® 3,
joka voidaan kirjoittaa kätevämmässä muodossa
Kaikille kahdelle tällaiselle muunnokselle S, T me päätämme S*T muunnoksena, joka on seurausta peräkkäisestä suorituksesta T, ja sitten S. Esimerkiksi jos , niin . Tällä määritelmällä kaikki 24 mahdollista muunnosa muodostavat ryhmän; sen identiteettielementti on , ja elementti käänteinen S, saadaan korvaamalla määritelmän nuolet S päinvastoin; esimerkiksi jos , niin .
Se on helppo nähdä kolmessa ensimmäisessä esimerkissä a*b = b*a; tällaisissa tapauksissa ryhmän tai ryhmän kertolaskua sanotaan kommutatiiviseksi. Toisaalta viimeisessä esimerkissä ja siten T*S eroaa S*T.
Esimerkin (d) ryhmä on erikoistapaus ns. symmetrinen ryhmä, jonka sovellusalaan kuuluvat mm. algebrallisten yhtälöiden ratkaisumenetelmät ja viivojen käyttäytyminen atomispektreissä. Esimerkkien (b) ja (c) ryhmillä on tärkeä rooli lukuteoriassa; esimerkissä (b) luku 4 voidaan korvata millä tahansa kokonaisluvulla n, ja numerot 0 - 3 - numerot 0 - 3 n– 1 (kun n= 12 saamme kellotauluissa olevien numeroiden järjestelmän, kuten edellä mainittiin); esimerkissä (c) luku 5 voidaan korvata millä tahansa alkuluvulla R, ja numerot 1 - 4 - numerot 1 - 4 p – 1.
Rakenteet ja isomorfismi.
Edelliset esimerkit osoittavat, kuinka vaihtelevaa ryhmän muodostavat objektit voivat olla luonteeltaan. Mutta itse asiassa kussakin tapauksessa kaikki johtuu samasta skenaariosta: objektijoukon ominaisuuksista otamme huomioon vain ne, jotka muuttavat tämän joukon ryhmäksi (tämä on esimerkki epätäydellisestä tiedosta!). Tällaisissa tapauksissa sanomme, että harkitsemme valitsemamme ryhmäkertoimen antamaa ryhmärakennetta.
Toinen esimerkki rakenteesta on ns. tilausrakenne. Paljon E jossa on järjestysrakenne tai järjestetty elementtien väliin a è b kuulua E, jokin relaatio on annettu, jota me merkitsemme R (a,b). (Tällaisen suhteen pitäisi olla järkevä mille tahansa elementtiparille E, mutta yleensä se on epätosi joillekin pareille ja totta toisille, esimerkiksi relaatio 7
(1) R (a,a) on totta jokaiselle mutta omistuksessa E;
(2) ulos R (a,b) Ja R (b,a) seuraa sitä a = b;
(3) ulos R (a,b) Ja R (b,c) pitäisi R (a,c).
Otetaanpa joitain esimerkkejä valtavasta määrästä erilaisia tilattuja sarjoja.
(mutta) E koostuu kaikista kokonaisluvuista, R (a,b) on suhde " mutta Pienempi kuin tai yhtä suuri kuin b».
(b) E koostuu kaikista kokonaisluvuista >1, R (a,b) on suhde " mutta jakaa b tai yhtä suuri b».
(c) E koostuu kaikista tasossa olevista ympyröistä, R (a,b) – suhde "ympyrä a sisältyvät b tai sopii yhteen b».
Viimeisenä esimerkkinä rakenteesta mainitaan metrisen avaruuden rakenne; tällainen rakenne on annettu kuvauksessa E, jos jokainen elementtipari a Ja b kuulua E, voit vastata numeroon d (a,b) i 0, joka täyttää seuraavat ominaisuudet:
(1) d (a,b) = 0 jos ja vain jos a = b;
(2) d (b,a) = d (a,b);
(3) d (a,c) Ј d (a,b) + d (b,c) mille tahansa kolmelle tietylle elementille a, b, c alkaen E.
Otetaan esimerkkejä metriavaruuksista:
(a) tavallinen "kolmiulotteinen" avaruus, jossa d (a,b) on tavallinen (tai "euklidinen") etäisyys;
(b) pallon pinta, jossa d (a,b) on kahta pistettä yhdistävän ympyrän pienimmän kaaren pituus a Ja b alalla;
c) mikä tahansa sarja E, mille d (a,b) = 1 jos a № b; d (a,a) = 0 mille tahansa elementille a.
Rakenteen käsitteen tarkka määrittely on melko vaikeaa. Yksityiskohtiin menemättä voimme sanoa sen kuvauksissa E tietyn tyyppinen rakenne annetaan, jos joukon elementtien välissä E(ja joskus muita objekteja, esimerkiksi numeroita, joilla on apurooli) annetaan suhteita, jotka täyttävät jonkin kiinteän aksioomijoukon, joka luonnehtii tarkasteltavan tyypin rakennetta. Yllä olemme antaneet kolmen tyyppisten rakenteiden aksioomat. Tietenkin on monia muita rakenteita, joiden teoriat ovat täysin kehittyneet.
Monet abstraktit käsitteet liittyvät läheisesti rakenteen käsitteeseen; Mainitsekaamme vain yksi tärkeimmistä - isomorfismin käsite. Muista esimerkki ryhmistä (b) ja (c) edellisestä osiosta. Se on helppo tarkistaa välilehdestä. 1 pöytään. 2 voidaan navigoida hakutoiminnolla
0 ® 1, 1 ® 2, 2 ® 4, 3 ® 3.
Tässä tapauksessa sanomme, että annetut ryhmät ovat isomorfisia. Yleensä kaksi ryhmää G Ja Gў ovat isomorfisia, jos ryhmän elementtien välillä G ja ryhmäelementtejä G¢ on mahdollista muodostaa tällainen henkilökohtainen vastaavuus a « a¢ entä jos c = a*b, sitten cў = aў* b¢ asiaankuuluville elementeille Gў. Mikä tahansa ryhmäteorian väite, joka pätee ryhmälle G, on edelleen voimassa ryhmälle G¢ ja päinvastoin. Algebrallisesti ryhmät G Ja G¢ erottamaton.
Lukija näkee helposti, että täsmälleen samalla tavalla voidaan määritellä kaksi isomorfista järjestettyä joukkoa tai kaksi isomorfista metriavaruutta. Voidaan osoittaa, että isomorfismin käsite ulottuu kaikentyyppisiin rakenteisiin.
LUOKITTELU
Vanhat ja uudet matematiikan luokitukset.
Rakenteen käsite ja muut siihen liittyvät käsitteet ovat ottaneet keskeisen paikan modernissa matematiikassa niin puhtaasti "teknisesti" kuin filosofisesti ja metodologisestikin. Rakenteiden päätyyppien yleiset lauseet toimivat erittäin tehokkaina matemaattisen "tekniikan" työkaluina. Aina kun matemaatikko onnistuu osoittamaan, että hänen tutkimansa objektit täyttävät tietyn tyyppisen rakenteen aksioomat, hän osoittaa siten, että kaikki tämäntyyppisen rakenneteorian lauseet pätevät hänen tutkimiinsa tiettyihin objekteihin (ilman näitä yleislauseita hän erittäin todennäköisesti jäävät poissa niiden erityisistä muunnelmista tai joutuisivat rasittamaan perustelunsa tarpeettomilla olettamuksilla). Vastaavasti, jos kaksi rakennetta osoitetaan isomorfisiksi, lauseiden määrä kaksinkertaistuu välittömästi: jokainen yhdelle rakenteelle todistettu lause antaa välittömästi vastaavan lauseen toiselle. Siksi ei ole yllättävää, että on olemassa hyvin monimutkaisia ja vaikeita teorioita, esimerkiksi lukuteorian "luokkakenttäteoria", jonka päätarkoituksena on todistaa rakenteiden isomorfismi.
Filosofisesta näkökulmasta katsottuna rakenteiden ja isomorfismien laaja käyttö osoittaa modernin matematiikan pääpiirteen - sen, että matemaattisten "objektien" "luonteella" ei ole oikeastaan väliä, vain objektien väliset suhteet ovat merkittäviä (eräänlainen epätäydellisen tiedon periaate).
Lopuksi on mahdotonta puhua siitä, että rakenteen käsite mahdollisti matematiikan osien luokittelun uudella tavalla. 1800-luvun puoliväliin asti. ne vaihtelivat tutkimuksen kohteen mukaan. Aritmetiikka (tai lukuteoria) käsitteli kokonaislukuja, geometria suoria, kulmia, polygoneja, ympyröitä, alueita ja niin edelleen. Algebra käsitteli lähes yksinomaan menetelmiä numeeristen yhtälöiden tai yhtälöjärjestelmien ratkaisemiseksi, analyyttinen geometria kehitti menetelmiä geometristen ongelmien muuttamiseksi vastaaviksi algebrallisiksi ongelmiksi. Toisen tärkeän matematiikan haaran, "matemaattisen analyysin", kiinnostuksen kohteet käsittivät pääasiassa differentiaali- ja integraalilaskennan ja niiden erilaiset sovellukset geometriassa, algebrassa ja parillisten lukuteoriassa. Näiden sovellusten määrä lisääntyi ja niiden merkitys myös kasvoi, mikä johti matemaattisen analyysin jakamiseen alaosiin: funktioteoria, differentiaaliyhtälöt (tavalliset ja osittaiset derivaatat), differentiaaligeometria, variaatiolaskenta jne.
Monille nykyajan matemaatikoille tämä lähestymistapa muistuttaa ensimmäisten luonnontieteilijöiden suorittaman eläinten luokittelun historiaa: kerran sekä merikilpikonnaa että tonnikalaa pidettiin kaloissa, koska ne elivät vedessä ja niillä oli samanlaisia piirteitä. Moderni lähestymistapa on opettanut meidät näkemään paitsi mitä pinnalla on, myös katsomaan syvemmälle ja yrittämään tunnistaa perusrakenteet, jotka piilevät matemaattisten esineiden petollisen ulkonäön takana. Tästä näkökulmasta on tärkeää tutkia tärkeimmät rakennetyypit. On epätodennäköistä, että meillä on käytettävissämme täydellinen ja lopullinen luettelo näistä tyypeistä; osa niistä on löydetty viimeisten 20 vuoden aikana, ja on syytä odottaa lisää löytöjä tulevaisuudessa. Meillä on kuitenkin jo käsitys monista "abstrakteista" perusrakenteista. (Ne ovat "abstrakteja" verrattuna "klassisiin" matematiikan esineisiin, vaikka niitäkin tuskin voidaan kutsua "konkreettisiksi"; kyse on pikemminkin abstraktioasteesta.)
Tunnetut rakenteet voidaan luokitella niiden sisältämien suhteiden tai monimutkaisuuden mukaan. Toisaalta on olemassa laaja "algebrallisten" rakenteiden lohko, jonka erikoistapaus on esimerkiksi ryhmärakenne; muiden algebrallisten rakenteiden joukossa nimeämme renkaita ja kenttiä ( cm. myös ALGEBRAN TIIVISTELMÄ). Algebrallisten rakenteiden tutkimiseen liittyvää matematiikan haaraa on kutsuttu "moderniksi algebraksi" tai "abstraktiksi algebraksi" tavallisen tai klassisen algebran vastakohtana. Merkittävä osa euklidisesta geometriasta, ei-euklidisesta geometriasta ja analyyttisestä geometriasta tuli myös osaksi uutta algebraa.
On olemassa kaksi muuta rakennelohkoa samalla yleisyyden tasolla. Yksi niistä, nimeltään yleinen topologia, sisältää teorioita rakennetyypeistä, joiden erityistapaus on metrisen avaruuden rakenne ( cm. TOPOLOGIA; abstraktit tilat). Kolmas lohko koostuu järjestysrakenteiden teorioista ja niiden laajennuksista. Rakenteen "laajentaminen" koostuu uusien lisäämisestä olemassa oleviin aksioomeihin. Jos esimerkiksi lisäämme kommutatiivisuuden ominaisuuden ryhmän aksioomeihin neljänneksi aksioomaksi a*b = b*a, niin saamme kommutatiivisen (tai abelilaisen) ryhmän rakenteen.
Näistä kolmesta lohkosta kaksi viimeistä olivat viime aikoihin asti suhteellisen vakaassa tilassa, ja "moderni algebra" -lohko kasvoi nopeasti, joskus odottamattomiin suuntiin (esimerkiksi kehitettiin kokonainen haara, jota kutsutaan "homologiseksi algebraksi"). Ulkopuolella ns. "puhtaat" rakenteiden tyypit ovat toinen taso - "sekoitetut" rakenteet, esimerkiksi algebralliset ja topologiset, yhdessä niitä yhdistävien uusien aksioomien kanssa. Monia tällaisia yhdistelmiä on tutkittu, joista useimmat jakautuvat kahteen laajaan lohkoon - "topologiseen algebraan" ja "algebralliseen topologiaan".
Yhdessä nämä lohkot muodostavat tilavuudeltaan erittäin vankan "abstraktin" tieteenalan. Monet matemaatikot toivovat ymmärtävänsä paremmin klassisia teorioita ja ratkaisevansa vaikeita ongelmia uusilla työkaluilla. Todellakin, sopivalla abstraktio- ja yleistystasolla muinaisten ongelmat voivat ilmaantua uudessa valossa, mikä mahdollistaa niiden ratkaisujen löytämisen. Valtavat palaset klassista materiaalia joutuivat uuden matematiikan vaikutuksen alaisuuteen ja muunnettiin tai yhdistettiin muihin teorioihin. Vielä on laajoja alueita, joille nykyaikaiset menetelmät eivät ole tunkeutuneet niin syvälle. Esimerkkejä ovat differentiaaliyhtälöiden teoria ja merkittävä osa lukuteoriaa. On hyvin todennäköistä, että näillä alueilla saavutetaan merkittävää edistystä, kun uudentyyppisiä rakenteita löydetään ja tutkitaan huolellisesti.
FILOSOFIASIA VAIKEUTEITA
Jo muinaiset kreikkalaiset ymmärsivät selvästi, että matemaattisen teorian tulisi olla vapaa ristiriitaisuuksista. Tämä tarkoittaa, että väitettä on mahdotonta päätellä loogisena seurauksena aksioomista R ja sen kieltäminen P. Koska uskottiin kuitenkin, että matemaattisilla esineillä on vastaavuudet todellisessa maailmassa ja aksioomit ovat luonnonlakien "idealisaatioita", kenelläkään ei ollut epäilystäkään matematiikan johdonmukaisuudesta. Siirtyessä klassisesta matematiikasta moderniin matematiikkaan johdonmukaisuusongelma sai toisen merkityksen. Vapautta valita minkä tahansa matemaattisen teorian aksioomat täytyy selvästi rajoittaa johdonmukaisuusehto, mutta onko mahdollista olla varma, että tämä ehto täyttyy?
Olemme jo maininneet sarjan käsitteen. Tätä käsitettä on aina käytetty enemmän tai vähemmän eksplisiittisesti matematiikassa ja logiikassa. 1800-luvun jälkipuoliskolla joukon käsitteen käsittelyn perussäännöt systematisoitiin osittain, lisäksi saatiin tärkeitä tuloksia, jotka muodostivat sisällön ns. joukko teoria ( cm. myös JOUKKOTEORIA), josta on tullut ikään kuin kaikkien muiden matemaattisten teorioiden alusta. Antiikista 1800-luvulle. äärettömiä joukkoja pelättiin esimerkiksi Zenon Elealaisen (5. vuosisadalla eKr.) kuuluisissa paradokseissa. Nämä pelot olivat osittain metafyysisiä ja osittain johtuivat suureiden mittauskäsitteeseen liittyvistä vaikeuksista (esimerkiksi pituus tai aika). Vasta 1800-luvun jälkeen nämä vaikeudet poistettiin. matemaattisen analyysin peruskäsitteet määriteltiin tiukasti. Vuoteen 1895 mennessä kaikki pelot hälvenivät, ja näytti siltä, että matematiikka lepää horjumattomalla joukkoteorian perustalla. Mutta seuraavan vuosikymmenen aikana syntyi uusia väitteitä, jotka näyttivät osoittavan joukkoteorian (ja kaiken muun matematiikan) luontaisen epäjohdonmukaisuuden.
Uudet paradoksit olivat hyvin yksinkertaisia. Näistä ensimmäistä - Russellin paradoksia - voidaan pitää yksinkertaisena versiona, joka tunnetaan nimellä "parturi paradoksi". Tietyssä kaupungissa parturi ajelee kaikki asukkaat, jotka eivät ajele itseään. Kuka ajaa parturin itse? Jos parturi ajelee itsensä, hän ei ajele vain niitä asukkaita, jotka eivät ajele, vaan myös yhden asukkaan, joka ajelee itsensä; jos hän ei ajele itseään, niin hän ei ajele kaikkia kaupungin asukkaita, jotka eivät ajele itseään. Tämän tyyppinen paradoksi syntyy aina, kun tarkastellaan "kaikkien joukkojen joukon" käsitettä. Vaikka tämä matemaattinen objekti näyttää hyvin luonnolliselta, sen pohtiminen johtaa nopeasti ristiriitaisuuksiin.
Berryn paradoksi on vielä paljastavampi. Harkitse kaikkien venäläisten lauseiden joukkoa, jotka sisältävät enintään seitsemäntoista sanaa; venäjän kielen sanojen määrä on rajallinen, joten myös tällaisten lauseiden määrä on rajallinen. Valitsemme niistä ne, jotka määrittelevät yksiselitteisesti jonkin kokonaisluvun, esimerkiksi: "Suurin pariton luku alle kymmenen." Tällaisten lauseiden määrä on myös rajallinen; näin ollen myös niiden määrittelemä kokonaislukujoukko on äärellinen. Merkitse näiden lukujen äärellinen joukko D. Aritmetiikan aksioomista seuraa, että on kokonaislukuja, jotka eivät kuulu joukkoon D, ja että näiden lukujen joukossa on pienin luku n. Tämä numero n on yksilöllisesti määritelty lauseella: "Pienin kokonaisluku, jota ei voida määritellä lauseella, joka koostuu enintään seitsemästätoista venäläisestä sanasta." Mutta tämä lause sisältää tarkalleen seitsemäntoista sanaa. Siksi se määrittää numeron n, jonka pitäisi kuulua D, ja tulemme paradoksaaliseen ristiriitaan.
Intuitionistit ja formalistit.
Joukkoteorian paradoksien aiheuttama shokki sai aikaan erilaisia reaktioita. Jotkut matemaatikot olivat melko määrätietoisia ja ilmaisivat mielipiteensä, että matematiikka kehittyi alusta alkaen väärään suuntaan ja sen pitäisi perustua täysin eri perustalle. Tällaisten "intuitionistien" (kuten he alkoivat kutsua itseään) näkökulmaa ei ole mahdollista kuvata tarkasti, koska he kieltäytyivät pelkistämästä näkemyksiään puhtaasti loogiseen suunnitelmaan. Intuitionistien näkökulmasta on väärin soveltaa loogisia prosesseja objekteihin, jotka eivät ole intuitiivisesti esitettävissä. Ainoat intuitiivisesti selkeät objektit ovat luonnolliset luvut 1, 2, 3,... ja luonnollisten lukujen äärelliset joukot, jotka on "rakennettu" täsmälleen annettujen sääntöjen mukaan. Mutta edes sellaisiin esineisiin intuitionistit eivät sallineet kaikkien klassisen logiikan päätelmien soveltamista. He eivät esimerkiksi tunnistaneet sitä mistään lausunnosta R totta sekään R, tai ei- R. Tällaisilla rajallisilla käytettävissään olevilla keinoilla he välttyivät helposti "paradokseista", mutta niin tehdessään he heittivät yli laidan paitsi kaiken modernin matematiikan, myös merkittävän osan klassisen matematiikan tuloksista, ja niille, jotka olivat vielä jäljellä, uusia, piti löytää monimutkaisempia todisteita.
Valtaosa nykyajan matemaatikoista oli eri mieltä intuitionistien väitteistä. Ei-intuitionistit matemaatikot ovat huomanneet, että paradokseissa käytetyt argumentit poikkeavat huomattavasti tavallisessa joukkoteoriaa koskevassa matemaattisessa työssä käytetyistä argumenteista, ja siksi tällaiset väitteet tulisi sulkea pois laittomina vaarantamatta olemassa olevia matemaattisia teorioita. Toinen havainto oli, että "naiivissa" joukkoteoriassa, joka oli olemassa ennen "paradoksien" tuloa, ei kyseenalaistettu termien "joukko", "ominaisuus", "suhde" merkitystä - aivan kuten klassisessa geometriassa "intuitiivinen" tavallisten geometristen käsitteiden luonne. Näin ollen voidaan edetä samalla tavalla kuin geometriassa, nimittäin hylätä kaikki yritykset vedota "intuitioon" ja ottaa joukkoteorian lähtökohtana täsmällisesti muotoiltujen aksioomien järjestelmä. Ei kuitenkaan ole selvää, kuinka sellaiset sanat kuin "omaisuus" tai "suhde" voidaan riistää niiden tavanomaisesta merkityksestä; kuitenkin se on tehtävä, jos haluamme sulkea pois sellaiset väitteet kuin Berryn paradoksi. Menetelmässä pidättäydytään käyttämästä tavallista kieltä aksioomien tai lauseiden muotoilussa; vain lauseet, jotka on rakennettu nimenomaisen jäykkien sääntöjen mukaan, ovat sallittuja "ominaisuuksina" tai "relaatioina" matematiikassa ja osallistuvat aksioomien muotoiluun. Tätä prosessia kutsutaan matemaattisen kielen "formalisoinniksi" (tavallisen kielen moniselitteisyydestä johtuvien väärinkäsitysten välttämiseksi on suositeltavaa mennä askel pidemmälle ja korvata sanat itse erikoismerkeillä formalisoiduissa lauseissa, esimerkiksi korvaa konnektiivi "ja" symbolilla &, yhdistävä "tai" - symbolilla Ъ, "olemassa" symbolilla $ jne.). Matemaatikkoja, jotka hylkäsivät intuitionistien ehdottamat menetelmät, alettiin kutsua "formalisteiksi".
Alkuperäiseen kysymykseen ei kuitenkaan koskaan vastattu. Onko "aksiomaattinen joukkoteoria" vapaa ristiriitaisuuksista? D. Hilbert (1862-1943) ja hänen koulunsa tekivät 1920-luvulla uusia yrityksiä todistaa "muodollisten" teorioiden johdonmukaisuutta, ja niitä kutsuttiin "metamamatematiikaksi". Pohjimmiltaan metamatematiikka on "sovelletun matematiikan" haara, jossa kohteet, joihin matemaattista päättelyä sovelletaan, ovat formalisoidun teorian ehdotuksia ja niiden sijaintia todisteissa. Näitä lauseita on pidettävä vain tiettyjen vakiintuneiden sääntöjen mukaisesti valmistettuina symbolien aineellisina yhdistelminä ilman minkäänlaista viittausta näiden symbolien mahdolliseen "merkitykseen" (jos sellainen on). Shakkipeli voi toimia hyvänä vertauksena: symbolit vastaavat nappuloita, lauseet eri paikkoihin laudalla ja päätelmät nappuloiden liikkumisen sääntöihin. Formalisoidun teorian johdonmukaisuuden osoittamiseksi riittää osoittamaan, että tässä teoriassa mikään todiste ei pääty väitteeseen 0 Ei. 0. Matemaattisten argumenttien käyttöä voidaan kuitenkin vastustaa "metamamatemaattisessa" todistuksessa. matemaattinen teoria; jos matematiikka olisi epäjohdonmukaista, matemaattiset argumentit menettäisivät kaiken voimansa ja olisimme noidankehän tilanteessa. Vastatakseen näihin väitteisiin Hilbert salli käyttää metamatematiikassa hyvin rajoitettua matemaattista päättelyä, jota intuitionistit pitävät hyväksyttävinä. Kuitenkin K. Godel osoitti pian (1931), että aritmeettisen johdonmukaisuutta ei voida todistaa näin rajoitetuin keinoin, jos se on todella johdonmukaista (tämän artikkelin laajuus ei salli meidän esitellä nerokasta menetelmää, jolla tämä merkittävä tulos saatiin, ja sitä myöhempi metamatematiikan historia).
Yhteenvetona nykyisen ongelmatilanteen formalistisesta näkökulmasta on myönnettävä, että se ei ole kaukana ohi. Joukkokäsitteen käyttöä ovat rajoittaneet varaukset, jotka on tietoisesti lisätty tunnettujen paradoksien välttämiseksi, eikä ole takeita siitä, ettei aksiomatisoidussa joukkoteoriassa syntyisi uusia paradokseja. Aksiomaattisen joukkoteorian rajoitukset eivät kuitenkaan estäneet uusien toteuttamiskelpoisten teorioiden syntymistä.
MATEMIKA JA TODELLA MAAILMA
Huolimatta väitteistä matematiikan riippumattomuudesta, kukaan ei kiellä, että matematiikka ja fyysinen maailma liittyvät toisiinsa. Matemaattinen lähestymistapa klassisen fysiikan ongelmien ratkaisemiseen on tietysti edelleen voimassa. On myös totta, että erittäin tärkeällä matematiikan alueella, nimittäin differentiaaliyhtälöiden, tavallisten ja osittaisten derivaattojen teoriassa, fysiikan ja matematiikan vastavuoroinen rikastuminen on varsin hedelmällistä.
Matematiikasta on hyötyä mikromaailman ilmiöiden tulkinnassa. Matematiikan uudet "sovellukset" eroavat kuitenkin merkittävästi klassisista. Yksi fysiikan tärkeimmistä työkaluista on noussut todennäköisyysteoriaksi, jota aiemmin käytettiin lähinnä uhkapeli- ja vakuutusteoriassa. Matemaattiset objektit, jotka fyysikot yhdistävät "atomitiloihin" tai "siirtymiin", ovat luonteeltaan erittäin abstrakteja, ja matemaatikot esittelivät ja tutkivat niitä kauan ennen kvanttimekaniikan tuloa. On lisättävä, että ensimmäisten onnistumisten jälkeen ilmaantui vakavia vaikeuksia. Tämä tapahtui aikana, jolloin fyysikot yrittivät soveltaa matemaattisia ideoita kvanttiteorian hienompiin aspekteihin; Siitä huolimatta monet fyysikot odottavat edelleen uusia matemaattisia teorioita uskoen niiden auttavan heitä ratkaisemaan uusia ongelmia.
Matematiikka – tiede vai taide?
Vaikka sisällyttäisimmekin todennäköisyysteorian tai matemaattisen logiikan "puhtaan" matematiikkaan, käy ilmi, että alle 50 % tunnetuista matemaattisista tuloksista on tällä hetkellä muiden tieteiden käytössä. Mitä meidän pitäisi ajatella jäljellä olevasta puoliskosta? Toisin sanoen, mitkä ovat motiivit niiden matematiikan alueiden takana, jotka eivät liity fyysisten ongelmien ratkaisuun?
Olemme jo maininneet luvun irrationaalisuuden tyypillisenä tämän tyyppisten lauseiden edustajana. Toinen esimerkki on J.-L. Lagrangen (1736–1813) todistama lause. Tuskin on matemaatikkoa, joka ei kutsuisi häntä "tärkeäksi" tai "kauniiksi". Lagrangen lause sanoo, että mikä tahansa kokonaisluku, joka on suurempi tai yhtä suuri kuin yksi, voidaan esittää enintään neljän luvun neliöiden summana; esimerkiksi 23 = 3 2 + 3 2 + 2 2 + 1 2 . Nykytilanteessa on mahdotonta ajatella, että tämä tulos voisi olla hyödyllinen minkä tahansa kokeellisen ongelman ratkaisemisessa. On totta, että fyysikot käsittelevät kokonaislukuja nykyään paljon useammin kuin ennen, mutta kokonaisluvut, joilla he toimivat, ovat aina rajallisia (harvoin ylittävät muutaman sadan); siksi Lagrangen kaltainen lause voi olla "hyödyllinen" vain, jos sitä sovelletaan kokonaislukuihin, jotka eivät ylitä jotakin rajaa. Mutta heti kun rajoitamme Lagrangen lauseen muotoilua, se lakkaa heti kiinnostamasta matemaatikkoa, koska tämän lauseen koko vetovoima on sen sovellettavuus kaikkiin kokonaislukuihin. (On olemassa monia ehdotuksia kokonaisluvuista, joita tietokoneet voivat testata erittäin suurille lukuille, mutta niin kauan kuin yleistä näyttöä ei löydy, ne pysyvät hypoteettisina eivätkä kiinnosta ammattimatemaatikoita.)
Keskittyminen aiheisiin, jotka ovat kaukana välittömistä sovelluksista, ei ole epätavallista millä tahansa alalla, olipa kyseessä tähtitiede tai biologia, työskenteleville tutkijoille. Vaikka kokeellista tulosta voidaan jalostaa ja parantaa, matemaattinen todistus on aina lopullinen. Siksi on vaikea vastustaa kiusausta käsitellä matematiikkaa tai ainakin sitä osaa siitä, jolla ei ole mitään tekemistä "todellisuuden" kanssa. Matemaattisia ongelmia ei pakoteta ulkopuolelta, ja nykyajan näkökulmasta olemme täysin vapaita materiaalin valinnassa. Joitakin matemaattisia töitä arvioidessaan matemaatikoilla ei ole "objektiivisia" kriteerejä, ja he joutuvat luottamaan omaan "makuun". Maku vaihtelee suuresti ajasta, maasta, perinteistä ja yksilöistä riippuen. Modernissa matematiikassa on muotia ja "kouluja". Tällä hetkellä on olemassa kolme tällaista "koulua", joita kutsumme mukavuuden vuoksi "klassismiksi", "modernismiksi" ja "abstraktionismiksi". Ymmärtääksemme paremmin niiden välisiä eroja, analysoidaan erilaisia kriteerejä, joita matemaatikot käyttävät arvioidessaan lausetta tai lauseryhmää.
(1) Yleisen mielipiteen mukaan "kauniin" matemaattisen tuloksen tulisi olla ei-triviaali, ts. ei saa olla ilmeinen seuraus aksioomista tai aiemmin todistetuista lauseista; Todistuksessa on käytettävä jotain uutta ideaa tai vanhoja ideoita on sovellettava nerokkaasti. Toisin sanoen matemaatikolle ei itse tulos ole tärkeä, vaan prosessi, jolla hän voi voittaa sen saavuttamisessa kohtaamat vaikeudet.
(2) Jokaisella matemaattisella ongelmalla on oma historiansa, niin sanotusti "syntyperä", joka noudattaa samaa yleistä kaavaa, jolla minkä tahansa tieteen historia kehittyy: ensimmäisten onnistumisten jälkeen voi kulua tietty aika ennen kuin kysymykseen vastataan. poseerattu löytyy. Kun päätös on saatu, tarina ei lopu siihen, vaan tunnetut laajenemis- ja yleistysprosessit alkavat. Esimerkiksi edellä mainittu Lagrange-lause johtaa kysymykseen minkä tahansa kokonaisluvun esittämisestä kuutioiden summana, potenssien 4, 5 jne. Näin syntyy "varoitusongelma", joka ei ole vielä saanut lopullista ratkaisua. Lisäksi, jos olemme onnellisia, ratkaisemamme ongelma osoittautuu liittyväksi yhteen tai useampaan perusrakenteeseen, mikä puolestaan johtaa näihin rakenteisiin liittyviin uusiin ongelmiin. Vaikka alkuperäinen teoria lopulta "kuolisi", sillä on taipumus jättää jälkeensä lukuisia eläviä versoja. Nykyaikaiset matemaatikot kohtaavat niin valtavan ongelmien hajaantuvuuden, että vaikka kaikki yhteys kokeelliseen tieteeseen katkeaisikin, niiden ratkaiseminen kestäisi vielä useita vuosisatoja.
(3) Jokainen matemaatikko on yhtä mieltä siitä, että kun hänelle esitetään uusi ongelma, hänen velvollisuutensa on ratkaista se kaikin mahdollisin keinoin. Kun ongelma koskee klassisia matemaattisia objekteja (klassistit harvoin käsittelevät muuntyyppisiä esineitä), klassistit yrittävät ratkaista sen vain klassisilla keinoilla, kun taas toiset matemaatikot ottavat käyttöön "abstraktisempia" rakenteita käyttääkseen tehtävään liittyviä yleisiä lauseita. Tämä ero lähestymistavassa ei ole uusi. Alkaen 1800-luvulta. matemaatikot jakautuvat "taktikoihin", jotka pyrkivät löytämään puhtaasti voimakkaan ratkaisun ongelmaan, ja "strategeihin", jotka ovat alttiita kiertoteille, jotka mahdollistavat vihollisen murskaamisen pienillä voimilla.
(4) Olennainen osa lauseen "kauneutta" on sen yksinkertaisuus. Tietysti yksinkertaisuuden etsiminen kuuluu kaikkeen tieteelliseen ajatteluun. Mutta kokeilijat ovat valmiita sietämään "rumia ratkaisuja", jos vain ongelma ratkaistaan. Samoin matematiikassa klassistit ja abstraktionistit eivät ole kovin huolissaan "patologisten" tulosten ilmaantumisesta. Toisaalta modernistit menevät niin pitkälle, että he pitävät "patologioiden" ilmaantumista teoriassa oireena peruskäsitteiden epätäydellisyydestä.
Matemaattinen tietosanakirja - hakuteos kaikista matematiikan aloista. Encyclopedia perustuu matematiikan tärkeimpiä alueita käsitteleviin katsausartikkeleihin. Päävaatimus tämän tyyppisille artikkeleille on teorian nykytilan katsauksen mahdollinen täydellisyys ja esityksen mahdollisimman helppo saatavuus; Nämä artikkelit ovat yleensä vanhempien matematiikan opiskelijoiden, jatko-opiskelijoiden ja matematiikan lähialojen asiantuntijoiden sekä tietyissä tapauksissa matemaattisia menetelmiä työssään käyttävien muiden osaamisalojen asiantuntijoiden, matematiikan insinöörien ja opettajien saatavilla. Lisäksi tarjotaan keskikokoisia artikkeleita yksittäisistä matematiikan erityisongelmista ja menetelmistä; Nämä artikkelit on tarkoitettu kapeammalle lukijapiirille, joten niissä oleva esitys voi olla vähemmän saavutettavissa. Lopuksi on vielä yksi artikkelityyppi - lyhyet viittaukset-määritelmät. Encyclopedian viimeisen osan loppuun sijoitetaan aihehakemisto, joka sisältää paitsi kaikkien artikkeleiden otsikot, myös monia käsitteitä, joiden määritelmät annetaan kahden ensimmäisen tyypin artikkeleiden sisällä, kuten sekä tärkeimmät artikkeleissa mainitut tulokset. Useimpiin Encyclopedian artikkeleihin on liitetty viiteluettelo kunkin nimikkeen sarjanumeroineen, mikä mahdollistaa lainaamisen artikkeleiden teksteissä. Artikkelien lopussa (pääsääntöisesti) mainitaan kirjoittaja tai lähde, jos artikkeli on jo julkaistu aiemmin (useimmiten nämä ovat Suuren Neuvostoliiton tietosanakirjan artikkeleita). Artikkeleissa mainittujen ulkomaisten (paitsi muinaisten) tiedemiesten nimissä on latinalainen oikeinkirjoitus (jos lähdeluetteloon ei viitata).

Lataa ja lue Mathematical Encyclopedia, Volume 3, Vinogradov I.M., 1982
Matemaattinen tietosanakirja - hakuteos kaikista matematiikan aloista. Encyclopedia perustuu matematiikan tärkeimpiä alueita käsitteleviin katsausartikkeleihin. Päävaatimus tämän tyyppisille artikkeleille on teorian nykytilan katsauksen mahdollinen täydellisyys ja esityksen mahdollisimman helppo saatavuus; Nämä artikkelit ovat yleensä vanhempien matematiikan opiskelijoiden, jatko-opiskelijoiden ja matematiikan lähialojen asiantuntijoiden sekä tietyissä tapauksissa matemaattisia menetelmiä työssään käyttävien muiden osaamisalojen asiantuntijoiden, matematiikan insinöörien ja opettajien saatavilla. Lisäksi tarjotaan keskikokoisia artikkeleita yksittäisistä matematiikan erityisongelmista ja menetelmistä; Nämä artikkelit on tarkoitettu kapeammalle lukijapiirille, joten niissä oleva esitys voi olla vähemmän saavutettavissa. Lopuksi on vielä yksi artikkelityyppi - lyhyet viittaukset-määritelmät. Encyclopedian viimeisen osan loppuun sijoitetaan aihehakemisto, joka sisältää paitsi kaikkien artikkeleiden otsikot, myös monia käsitteitä, joiden määritelmät annetaan kahden ensimmäisen tyypin artikkeleiden sisällä, kuten sekä tärkeimmät artikkeleissa mainitut tulokset. Useimpiin Encyclopedian artikkeleihin on liitetty viiteluettelo kunkin nimikkeen sarjanumeroineen, mikä mahdollistaa lainaamisen artikkeleiden teksteissä. Artikkelien lopussa (pääsääntöisesti) mainitaan kirjoittaja tai lähde, jos artikkeli on jo julkaistu aiemmin (useimmiten nämä ovat Suuren Neuvostoliiton tietosanakirjan artikkeleita). Artikkeleissa mainittujen ulkomaisten (paitsi muinaisten) tiedemiesten nimissä on latinalainen oikeinkirjoitus (jos lähdeluetteloon ei viitata).
 Lataa ja lue Mathematical Encyclopedia, Volume 2, Vinogradov I.M., 1979
Lataa ja lue Mathematical Encyclopedia, Volume 2, Vinogradov I.M., 1979
Matemaattinen tietosanakirja - hakuteos kaikista matematiikan aloista. Encyclopedia perustuu matematiikan tärkeimpiä alueita käsitteleviin katsausartikkeleihin. Päävaatimus tämän tyyppisille artikkeleille on teorian nykytilan katsauksen mahdollinen täydellisyys ja esityksen mahdollisimman helppo saatavuus; Nämä artikkelit ovat yleensä vanhempien matematiikan opiskelijoiden, jatko-opiskelijoiden ja matematiikan lähialojen asiantuntijoiden sekä tietyissä tapauksissa matemaattisia menetelmiä työssään käyttävien muiden osaamisalojen asiantuntijoiden, matematiikan insinöörien ja opettajien saatavilla. Lisäksi tarjotaan keskikokoisia artikkeleita yksittäisistä matematiikan erityisongelmista ja menetelmistä; Nämä artikkelit on tarkoitettu kapeammalle lukijapiirille, joten niissä oleva esitys voi olla vähemmän saavutettavissa. Lopuksi on vielä yksi artikkelityyppi - lyhyet viittaukset-määritelmät. Encyclopedian viimeisen osan loppuun sijoitetaan aihehakemisto, joka sisältää paitsi kaikkien artikkeleiden otsikot, myös monia käsitteitä, joiden määritelmät annetaan kahden ensimmäisen tyypin artikkeleiden sisällä, kuten sekä tärkeimmät artikkeleissa mainitut tulokset. Useimpiin Encyclopedian artikkeleihin on liitetty viiteluettelo kunkin nimikkeen sarjanumeroineen, mikä mahdollistaa lainaamisen artikkeleiden teksteissä. Artikkelien lopussa (pääsääntöisesti) mainitaan kirjoittaja tai lähde, jos artikkeli on jo julkaistu aiemmin (useimmiten nämä ovat Suuren Neuvostoliiton tietosanakirjan artikkeleita). Artikkeleissa mainittujen ulkomaisten (paitsi muinaisten) tiedemiesten nimissä on latinalainen oikeinkirjoitus (jos lähdeluetteloon ei viitata).

Lataa ja lue Mathematical Encyclopedia, Volume 1, Vinogradov I.M., 1977
Algebra oli alun perin matematiikan haara, joka keskittyi yhtälöiden ratkaisemiseen. Toisin kuin geometria, algebran aksiomaattinen rakenne oli olemassa vasta 1800-luvun puolivälissä, jolloin syntyi pohjimmiltaan uusi näkemys algebran aiheesta ja luonteesta. Tutkimus alkoi keskittyä yhä enemmän niin kutsuttujen algebrallisten rakenteiden tutkimiseen. Tästä oli kaksi etua. Toisaalta selvennettiin alueita, joille tietyt lauseet ovat päteviä, toisaalta tuli mahdolliseksi käyttää samoja todisteita täysin eri alueilla. Tämä algebran jako kesti 1900-luvun puoliväliin asti ja ilmeni siinä, että ilmestyi kaksi nimeä: "klassinen algebra" ja "moderni algebra". Jälkimmäiselle on ominaista toinen nimi: "abstrakti algebra". Tosiasia on, että tälle osalle - ensimmäistä kertaa matematiikassa - oli ominaista täydellinen abstraktio.

Lataa ja lue Small Mathematical Encyclopedia, Fried E., Pastor I., Reiman I., Reves P., Ruja I., 1976
"Todennäköisyys ja matemaattiset tilastot" - hakuteos todennäköisyysteoriasta, matemaattisista tilastoista ja niiden sovelluksista tieteen ja teknologian eri aloilla. Tietosanakirjassa on kaksi osaa: pääosa sisältää katsausartikkeleita, yksittäisiin erityisongelmiin ja menetelmiin omistettuja artikkeleita, lyhyitä viitteitä peruskäsitteiden määritelmistä, tärkeimmistä lauseista ja kaavoista. Merkittävä paikka on annettu sovellettaville aiheille - informaatioteorialle, jonoteorialle, luotettavuusteorialle, kokeiden suunnittelulle ja niihin liittyville alueille - fysiikka, geofysiikka, genetiikka, demografia ja tietyt tekniikan osa-alueet. Useimpiin artikkeleihin on liitetty bibliografia tätä asiaa koskevista tärkeimmistä kirjoituksista. Artikkelien otsikot ovat myös englanninkielisinä käännöksinä. Toinen osa - "Todennäköisyysteorian ja matemaattisten tilastojen lukija" sisältää artikkeleita, jotka on kirjoitettu menneisyyden venäläisille tietosanakirjoille, sekä aiemmin muissa teoksissa julkaistuja tietosanakirjamateriaaleja. Tietosanakirjaan liittyy laaja lista todennäköisyysteorian ja matemaattisten tilastojen ongelmia käsittelevistä aikakauslehdistä, aikakausjulkaisuista ja meneillään olevista julkaisuista.
Tietosanakirjan aineisto on tarpeellinen matematiikan ja muiden tieteiden alan opiskelijoille, jatko-opiskelijoille ja tutkijoille, jotka käyttävät todennäköisyyslaskentaa tutkimuksessaan ja käytännön työssään.

Lataa kirja Mathematical Encyclopedia 5 osana täysin ilmainen.
Jos haluat ladata kirjan ilmaiseksi tiedostopalvelusta, napsauta linkkejä välittömästi ilmaisen kirjan kuvauksen jälkeen.
Matemaattinen tietosanakirja - hakuteos kaikista matematiikan aloista. Encyclopedia perustuu matematiikan tärkeimpiä alueita käsitteleviin katsausartikkeleihin. Päävaatimus tämän tyyppisille artikkeleille on teorian nykytilan katsauksen mahdollinen täydellisyys ja esityksen mahdollisimman helppo saatavuus; Nämä artikkelit ovat yleensä vanhempien matematiikan opiskelijoiden, jatko-opiskelijoiden ja matematiikan lähialojen asiantuntijoiden sekä tietyissä tapauksissa muiden matematiikan menetelmiä työssään käyttävien tietoalojen asiantuntijoiden, matematiikan insinöörien ja opettajien saatavilla. Lisäksi tarjotaan keskikokoisia artikkeleita yksittäisistä matematiikan erityisongelmista ja menetelmistä; Nämä artikkelit on tarkoitettu kapeammalle lukijapiirille, joten niissä oleva esitys voi olla vähemmän saavutettavissa. Lopuksi on vielä yksi artikkelityyppi - lyhyet viittaukset-määritelmät.
Hyvät lukijat, jos epäonnistutte
lataa matemaattinen tietosanakirja 5 osana
Kirjoita siitä kommentteihin ja autamme sinua varmasti.Matemaattinen tietosanakirja
Matemaattinen tietosanakirja- Neuvostoliiton tietosanakirjajulkaisu viidessä osassa, jotka on omistettu matemaattisille aiheille. Julkaisi vuonna -1985 kustantamo "Soviet Encyclopedia". Päätoimittaja: Akateemikko I. M. Vinogradov.
Tämä on perustavanlaatuinen kuvitettu painos kaikilla tärkeimmillä matematiikan aloilla. Kirja sisältää laajaa materiaalia aiheesta, kuuluisien matemaatikoiden elämäkertoja, piirroksia, kaavioita, kaavioita ja kaavioita.
Kokonaismäärä: noin 3000 sivua. Artikkelien jakautuminen määrien mukaan:
- Osa 1: Abacus - Huygensin periaate, 576 s.
- Osa 2: D'Alembert Operator - Yhteistyöpeli, 552 s.
- Osa 3: Koordinaatit - Monomial, 592 s.
- Osa 4: Lauseen silmä - Monimutkainen funktio, 608 s.
- Osa 5: Satunnainen muuttuja - Solu, 623 s.
Liite osaan 5: aihehakemisto, luettelo havaituista kirjoitusvirheistä.
Linkit
- Matematiikan yleiset ja erityiset hakuteokset ja tietosanakirjat World of Mathematical Equations -portaalissa, josta voit ladata tietosanakirjan sähköisessä muodossa.
Luokat:
- Kirjat aakkosjärjestyksessä
- Matemaattinen kirjallisuus
- tietosanakirjat
- Kustantajan "Soviet Encyclopedia" kirjat
- Neuvostoliiton tietosanakirja
Wikimedia Foundation. 2010 .
- Matemaattinen kemia
- Kvanttimekaniikan matemaattiset perusteet
Katso, mitä "Mathematical Encyclopedia" on muissa sanakirjoissa:
matemaattinen logiikka- (teoreettinen logiikka, symbolinen logiikka) matematiikan ala, joka tutkii matematiikan perusteiden todisteita ja kysymyksiä. "Nykyajan matemaattisen logiikan aihe on monipuolinen." P. S. Poretskyn määritelmän mukaan "matemaattinen ... ... Wikipedia
Tietosanakirja- (uusi lat. tietosanakirja (ei aikaisintaan 1500-luvulla) muusta kreikkalaisesta sanasta ἐγκύκλιος παιδεία "harjoittelu täydessä ympyrässä", κύκλος Wikipediaide ympyrä ja παίαδδ koulutuksen
TIETOSANAKIRJA- (kreikan kielestä. enkyklios paideia koulutus kaikella tietämyksellä), tieteellinen. tai tieteellinen suosittu hakuteos, joka sisältää systematizir. tietojoukko. E.:n materiaali on järjestetty aakkosjärjestykseen tai systemaattisesti. periaate (tiedonhaarojen mukaan). ... ... Luonnontiede. tietosanakirja
MATEMAATTINEN LOGIIKKA- yksi modernin logiikan nimistä, joka tuli toisessa. lattia. 19 aikaisin 20. vuosisata perinteisen logiikan sijaan. Termiä symbolinen logiikka käytetään myös toisena nimenä logiikkatieteen nykyaikaiselle kehitysvaiheelle. Määritelmä…… Filosofinen tietosanakirja
MATEMAATTINEN ÄTTÖMÄTÖN- yleinen nimi joulukuu äärettömyyden idean toteutuminen matematiikassa. Vaikka M. b.-käsitteen merkityksien välissä. ja muissa merkityksissä, joissa termiä ääretön käytetään, ei ole jäykkää rajaa (koska kaikki nämä käsitteet heijastavat lopulta hyvin ... ... Filosofinen tietosanakirja
MATEMAATTINEN INDUKTIO- täydellinen matemaattinen induktio (matematiikassa sitä kutsutaan usein yksinkertaisesti täydelliseksi induktioksi; tässä tapauksessa tämä käsite tulisi erottaa täydellisen induktion käsitteestä, jota tarkastellaan ei-matemaattisessa formaalilogiikassa), - menetelmä yleisten väitteiden todistamiseksi ... ... Filosofinen tietosanakirja
MATEMAATTINEN HYPOTEESI- tutkitun ilmiökentän lakia ilmaisevan yhtälön muodon, tyypin, luonteen väitetty muutos, jonka tarkoituksena on laajentaa se uuteen, vielä tutkimattomaan kenttään siihen ominaisena laina. M. on laajalti käytössä nykyaikaisessa. teoreettinen ... ... Filosofinen tietosanakirja
MATEMAATTINEN KOULU POLITIIKALLA- Englanti. poliittisen taloustieteen matemaattinen koulu; Saksan kieli matemaattinen kurssi poliittisissa Okonomieissä. 1800-luvun jälkipuoliskolla syntyneen politiikan, talouden suunnan sen edustajat (L. Walras, V. Pareto, O. Jevons jne.) antoivat ... ... Sosiologian tietosanakirja
SOSIOLOGIAN MATEMAATTISET KOULU- Englanti. sosiologian matemaattinen koulu; Saksan kieli Sosiologian matemaattinen koulu. Sosiologian suunta, joka syntyi 1900-luvun ensimmäisellä puoliskolla, jonka perustajat (A. Zipf, E. Dodd ja muut) uskoivat, että sosiologi, teoriat saavuttavat ... ... Sosiologian tietosanakirja
Rakennusten ja rakenteiden matemaattinen malli- Rakennusten ja rakenteiden matemaattinen (tietokone)malli - rakennusten ja rakenteiden esitys elementtikaavion muodossa numeerisia laskelmia varten ratkaistaessa suunnittelussa, rakentamisessa ja ... ... Rakennusmateriaalien termien, määritelmien ja selitysten tietosanakirja
Kirjat
- Matemaattinen tietosanakirja (5 kirjan sarja), . Mathematical Encyclopedia on kätevä hakuteos kaikista matematiikan aloista. Encyclopedia perustuu matematiikan tärkeimpiä alueita käsitteleviin artikkeleihin. Sijaintiperiaate...
Matemaattinen tietosanakirja - hakuteos kaikista matematiikan aloista. Encyclopedia perustuu matematiikan tärkeimpiä alueita käsitteleviin katsausartikkeleihin. Päävaatimus tämän tyyppisille artikkeleille on teorian nykytilan katsauksen mahdollinen täydellisyys ja esityksen mahdollisimman helppo saatavuus; Nämä artikkelit ovat yleensä vanhempien matematiikan opiskelijoiden, jatko-opiskelijoiden ja matematiikan lähialojen asiantuntijoiden sekä tietyissä tapauksissa muiden matematiikan menetelmiä työssään käyttävien tietoalojen asiantuntijoiden, matematiikan insinöörien ja opettajien saatavilla. Lisäksi tarjotaan keskikokoisia artikkeleita yksittäisistä matematiikan erityisongelmista ja menetelmistä; Nämä artikkelit on tarkoitettu kapeammalle lukijapiirille, joten niissä oleva esitys voi olla vähemmän saavutettavissa. Lopuksi on vielä yksi artikkelityyppi - lyhyet viittaukset-määritelmät. Jotkut määritelmät annetaan kahden ensimmäisen artikkelityypin sisällä. Useimpiin Encyclopedian artikkeleihin on liitetty viiteluettelo kunkin nimikkeen sarjanumeroineen, mikä mahdollistaa lainaamisen artikkeleiden teksteissä. Artikkelien lopussa (pääsääntöisesti) mainitaan kirjoittaja tai lähde, jos artikkeli on jo julkaistu aiemmin (useimmiten nämä ovat Suuren Neuvostoliiton tietosanakirjan artikkeleita). Artikkeleissa mainittujen ulkomaisten (paitsi muinaisten) tiedemiesten nimissä on latinalainen oikeinkirjoitus (jos lähdeluetteloon ei viitata).
Tietosanakirjan artikkelien järjestyksen periaate on aakkosellinen. Jos artikkelin otsikko on termi, jolla on synonyymi, jälkimmäinen annetaan pääsanan jälkeen. Monissa tapauksissa artikkelien otsikot koostuvat kahdesta tai useammasta sanasta. Näissä tapauksissa termit annetaan joko yleisimmässä muodossa tai merkityksen pääsana asetetaan etusijalle. Jos artikkelin otsikossa on erisnimi, se sijoitetaan ensimmäiseksi (tällaisten artikkelien lähdeluettelossa on pääsääntöisesti päälähde, joka selittää termin nimen). Artikkelien otsikot annetaan pääosin yksikkömuodossa.
Tietosanakirjassa käytetään laajalti linkkijärjestelmää muihin artikkeleihin, joista lukija löytää lisätietoa käsiteltävään aiheeseen. Määritelmä ei viittaa artikkelin otsikossa olevaan termiin.
Tilan säästämiseksi artikkeleissa käytetään joidenkin tietosanakirjojen tavanomaisia lyhenteitä.
Työskenteli volyymilla 1
Neuvostoliiton Encyclopedia Publishing Housen matematiikan toimituskunta - V. I. BITYUTSKOV (toimituslautakunnan johtaja), M. I. VOITSEHOVSKY (tieteellinen toimittaja), Yu. A. GORBKOV (tieteellinen toimittaja), A. B. IVANOV (vanhempi tieteellinen toimittaja), O A. IVANOVA vanhempi tieteellinen toimittaja), T. Yu. L. R. KHABIB (apulaistoimittaja).
Kustantajan työntekijät: E. P. RYABOVA (kirjallinen toimituskunta). E. I. ZHAROVA, A. M. MARTYNOV (bibliografia). A. F. DALKOVSKY (transkriptio). N. A. FEDOROV (hankintaosasto). 3. A. SUKHOVA (Toimitukselliset kuvat). E. I. ALEKSEEVA, N. YU. KRUŽALOV (editointisanakirja). M. V. AKIMOVA, A. F. PROSHKO (oikoluku). G. V. SMIRNOV (tekninen painos).
Kansikuva taiteilija R. I. MALANICHEV.
Lisätietoa osasta 1
Kustantaja "Soviet Encyclopedia"
Encyclopedias sanakirjat hakuteoksia
Tieteellinen - Kustantajan toimituskunta
A. M. PROKHOROV (puheenjohtaja), I. V. ABASHIDZE, P. A. AZIMOV, A. P. ALEKSANDROV, V. A. AMBARTZUMYAN, I. I. ARTOBOLEVSKY, A. V. ARTSIKHOVSKY, M. S. ASIMOV, N Uv Yunov, M. S. ASIMOV, N. Uvsky, M. S. ASIMOV, N. U.v., M. S. ASIMOV, N. U.v., M. S. ASIMOV, N. Uv. , VV Volsky, BM Vul, BG Gafurov, SR Gershberg, MS Gilyarov, varapuheenjohtaja Glushko, VM Glushkov, G. N GOLIKOV, DB GULIEV, AA GUSEV (varapuheenjohtaja), varapuheenjohtaja ELYUTIN, VS EMELYANOV, EM ZHUKOVNETSKY, AA, IMSHELYANOV INOZEMTSEV, M I. Kabachnik, S. V. Kalesnik, G. A. Karavaev, K. K. Karakeev, M. K. Karataev, B. M. Kedrov, G. V. Keldysh, V. A. Kirillin ja I. L KNUNYANTS, SM KOVALEV (ensimmäinen varapuheenjohtaja), F., V. V. K. V. K. (varapuheenjohtaja), BV KUKARKIN, VG KULIKOV, I. A. Kutuzov, P. P. Lobanov, G. M. Loza, Yu. E. Maksarev, P. A. Markov, A. I. Markushevich, Yu. Yu. Obichkin, B. E. Paton, V. M. Polevo J, M. A. Prokofjev, Yu. V. Prokhorov, N. F. Rostovtsev, A. M. Rumjantsev, B. A. Rybakov, V. P. Samson, M. I. Sladkovski, V. I. Smirnov, DN SOLOVIEV (varapuheenjohtaja), VG SOLODOVNILINKOV, VN A. SOLODOVNIKOV, VN A. SLODOVNIKOV, V. , SA TOKAREV, VA Trapeznikov, E. K. Fedorov, M. B. Khrapchenko, E. I. Chazov, V. N. Chernigovskii, Ya. E. Shmushkis ja S. I. Yutkevich Neuvoston sihteeri L. V. KIRILLOVA.
Moskova 1977
Matemaattinen tietosanakirja. Osa 1 (A–D)
Päätoimittaja I. M. VINOGRADOV
Toimitusryhmä
S. I. ADYAN, P. S. ALEKSANDROV, N. S. BAKHVALOV, V. I. BITYUTSKOV (apulaispäätoimittaja), A. V. BITSADZE, L. N. BOLSHEV, A. A. GONCHAR, N. V. Efimov, VA Ilyin, A. A. Karavilišn, Mišdšentsunsu, A. SP Novikov, ja EG Poznyak, Yu. V. PROKHOROV (apulaispäätoimittaja), A. G. SVESHNIKOV, A. N. TIHONOV, P. L. ULYANOV, A. I. SHIRSHOV, S. V. YABLONSKY
Matemaattinen tietosanakirja. Ed. kollegio: I. M. Vinogradov (toimittajan päällikkö) [ja muut] T. 1 - M., "Soviet Encyclopedia", 1977
(Encyclopedias. Dictionaries. Reference books), vol. 1. A - G. 1977. 1152 jne. sairaalta.
Luovutettu sarjaan 9. 06. 1976. Allekirjoitettu painoon 18. 02. 1977. Tekstin tulostus Ensimmäisessä Esimerkkipainossa tehdyistä matriiseista. A. A. Zhdanova. Työn punaisen lipun ritarikunta, kustantamo "Soviet Encyclopedia". 109817. Moscow, Zh - 28, Pokrovsky Boulevard, 8. T - 02616 Levikki 150 000 kappaletta. Tilausnro 418. Painopaperi nro 1. Paperikoko 84xl08 1/14. Volume 36 fyysinen p. l. ; 60, 48 konv. p. l. teksti. 101, 82 tiliä - toim. l. Kirjan hinta on 7 ruplaa. 10 k.
Työn punaisen lipun määräys Moskovan kirjapaino nro 1 "Sojuzpoligrafprom" Neuvostoliiton ministerineuvoston julkaisu-, paino- ja kirjakaupan valtiokomitean alaisuudessa, Moskova, I-85, Prospekt Mira, 105. Tilaus nro. 865.
20200 - 004 allekirjoitettu © Kustantaja "Soviet Encyclopedia", 1977 007(01) - 77
 Balabol, balabolit, blah blah - etymologia Balabol mikä tarkoittaa
Balabol, balabolit, blah blah - etymologia Balabol mikä tarkoittaa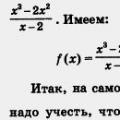 Aperture: mikä se on ja miksi se on tärkeä älypuhelimelle?
Aperture: mikä se on ja miksi se on tärkeä älypuhelimelle?