نحوه محاسبه ماتریس معکوس ماتریس معکوس را به صورت آنلاین پیدا کنید. با استفاده از ماشین حساب

جبر ماتریسی - ماتریس معکوس

ماتریس معکوس

ماتریس معکوسماتریسی نامیده می شود که وقتی در سمت راست و چپ در یک ماتریس معین ضرب شود، ماتریس هویت به دست می آید.
ماتریس را معکوس به ماتریس نشان دهید ولیاز طریق ، سپس طبق تعریف به دست می آوریم:

جایی که Eماتریس هویت است.
ماتریس مربعتماس گرفت غیر خاص (غیر منحط) اگر تعیین کننده آن برابر با صفر نباشد. در غیر این صورت نامیده می شود خاص (منحط) یا مفرد.

یک قضیه وجود دارد: هر ماتریس غیر مفرد یک ماتریس معکوس دارد.

عملیات یافتن ماتریس معکوس نامیده می شود درخواستماتریس ها الگوریتم وارونگی ماتریس را در نظر بگیرید. اجازه دهید یک ماتریس غیر مفرد داده شود n- مرتبه:

جایی که Δ = det آ ≠ 0.

مکمل عنصر جبریماتریس ها n- مرتبه ولیتعیین کننده ماتریس ( n–1)-ام سفارش به دست آمده با حذف من-خط و jستون -ام ماتریس ولی:

بیایید به اصطلاح ایجاد کنیم پیوست شده استماتریس:

مکمل های جبری عناصر مربوطه ماتریس کجا هستند ولی.
توجه داشته باشید که مکمل های جبری عناصر ردیف ماتریس ولیدر ستون های مربوطه ماتریس قرار می گیرند Ã ، یعنی ماتریس به طور همزمان جابجا می شود.
تقسیم تمام عناصر ماتریس Ã روی Δ - مقدار تعیین کننده ماتریس ولی، ماتریس معکوس را در نتیجه بدست می آوریم:

ما تعدادی از خواص ویژه ماتریس معکوس را یادداشت می کنیم:
1) برای یک ماتریس معین ولیماتریس معکوس آن تنها است؛
2) اگر ماتریس معکوس وجود داشته باشد، پس سمت راست معکوسو سمت چپ معکوسماتریس ها با آن منطبق هستند.
3) یک ماتریس مربع ویژه (محوول) ماتریس معکوس ندارد.

ویژگی های اصلی ماتریس معکوس:
1) تعیین کننده ماتریس معکوس و تعیین کننده ماتریس اصلی متقابل هستند.
2) ماتریس معکوس حاصل ضرب ماتریس های مربع برابر است با حاصلضرب ماتریس معکوس عوامل به ترتیب معکوس:

3) ماتریس معکوس انتقالی برابر با ماتریس معکوس از ماتریس انتقال داده شده است:

مثال معکوس ماتریس داده شده را محاسبه کنید.

ماتریس معکوسیک ماتریس است A -1، وقتی در آن ماتریس اولیه داده شده ضرب شود آماتریس هویت را می دهد E:

AA -1 = A -1 A =E.

روش ماتریس معکوس

روش ماتریس معکوس- این یکی از متداول ترین روش ها برای حل ماتریس است و برای آن استفاده می شود حل سیستم های معادلات جبری خطی(SLAE) در مواردی که تعداد مجهولات با تعداد معادلات مطابقت دارد.

بگذار یک سیستم وجود داشته باشد nمعادلات خطی با nناشناس:

چنین سیستمی را می توان به صورت یک معادله ماتریسی نوشت A*X=B,

جایی که
- ماتریس سیستم،

- ستون مجهولات،

- ستون ضرایب آزاد.

از معادله ماتریس مشتق شده، X را با ضرب دو طرف معادله ماتریس در سمت چپ در بیان می کنیم. الف-1، منجر به:

A -1 * A * X = A -1 * B

با دانستن اینکه A-1*A=E، سپس E*X=A-1*Bیا X=A-1*B.

مرحله بعدی تعیین ماتریس معکوس است الف-1و در ستون اعضای آزاد ضرب می شود ب.

ماتریس معکوس به ماتریس آتنها زمانی وجود دارد که دت ا≠ 0 . با توجه به این موضوع، هنگام حل SLAE با روش ماتریس معکوس، اولین قدم یافتن است دت ا. اگر یک دت ا≠ 0 ، پس سیستم فقط یک جواب دارد که با روش ماتریس معکوس می توان آن را به دست آورد، اگر det A = 0، سپس چنین سیستمی روش ماتریس معکوسحل نمی شود.

راه حل ماتریس معکوس

توالی اقدامات برای راه حل های ماتریس معکوس:

1. تعیین کننده ماتریس را بدست آورید آ. اگر تعیین کننده بزرگتر از صفر باشد، ماتریس معکوس را بیشتر حل می کنیم، اگر برابر با صفر باشد، در اینجا ماتریس معکوس پیدا نمی شود.
2. یافتن ماتریس جابجا شده AT.
3. ما به دنبال متمم های جبری می گردیم، پس از آن همه عناصر ماتریس را با مکمل های جبری آنها جایگزین می کنیم.
4. ماتریس معکوس را از اضافات جبری جمع آوری می کنیم: همه عناصر ماتریس حاصل را بر تعیین کننده ماتریس اولیه داده شده تقسیم می کنیم. ماتریس نهایی ماتریس معکوس مطلوب نسبت به ماتریس اصلی خواهد بود.

الگوریتم زیر راه حل های ماتریس معکوساساساً مانند بالا است، تفاوت فقط در چند مرحله است: اول از همه، جمع های جبری را تعیین می کنیم و پس از آن ماتریس اتحاد را محاسبه می کنیم. سی.

1. دریابید که آیا ماتریس داده شده مربع است یا خیر. در صورت پاسخ منفی، مشخص می شود که ماتریس معکوس برای آن وجود ندارد.
2. دریابید که آیا ماتریس داده شده مربع است یا خیر. در صورت پاسخ منفی، مشخص می شود که ماتریس معکوس برای آن وجود ندارد.
3. ما جمع های جبری را محاسبه می کنیم.
4. ما ماتریس متحد (متقابل، پیوست) را می سازیم سی.
5. ما یک ماتریس معکوس از اضافات جبری می سازیم: همه عناصر ماتریس الحاقی سیتقسیم بر تعیین کننده ماتریس اولیه. ماتریس حاصل، ماتریس معکوس مورد نظر نسبت به ماتریس داده شده خواهد بود.
6. ما کار انجام شده را بررسی می کنیم: ماتریس های اولیه و حاصل را ضرب می کنیم، نتیجه باید ماتریس هویت باشد.

این به بهترین وجه با یک ماتریس پیوست انجام می شود.

قضیه: اگر ماتریس هویتی با همان ترتیب را به یک ماتریس مربع در سمت راست نسبت دهیم و ماتریس اولیه سمت چپ را با استفاده از تبدیل های اولیه روی ردیف ها به ماتریس واحد تبدیل کنیم، آنگاه ماتریس به دست آمده در سمت راست معکوس خواهد بود. اولیه

نمونه ای از یافتن ماتریس معکوس.

ورزش. برای ماتریس معکوس را با روش ماتریس الحاقی پیدا کنید.

تصمیم گیری به ماتریس داده شده اضافه می کنیم ولیدر سمت راست، ماتریس هویت مرتبه دوم:

عدد 2 را از خط 1 کم کنید:

۲ عدد اول را از خط دوم کم کنید:

ماتریس $A^(-1)$ معکوس ماتریس مربع $A$ نامیده می شود اگر $A^(-1)\cdot A=A\cdot A^(-1)=E$، جایی که $E $ ماتریس هویت است که ترتیب آن برابر با ترتیب ماتریس $A$ است.

ماتریس غیر مفرد ماتریسی است که دترمینان آن برابر با صفر نباشد. بر این اساس، یک ماتریس منحط، ماتریسی است که دترمینانت آن برابر با صفر باشد.

ماتریس معکوس $A^(-1)$ وجود دارد اگر و فقط اگر ماتریس $A$ غیر مفرد باشد. اگر ماتریس معکوس $A^(-1)$ وجود داشته باشد، یکتا است.

راه های مختلفی برای یافتن معکوس یک ماتریس وجود دارد که ما به دو مورد از آنها می پردازیم. در این صفحه روش ماتریس الحاقی که در اکثر دروس ریاضیات عالی استاندارد در نظر گرفته می شود، بحث خواهد شد. راه دوم برای یافتن ماتریس معکوس (روش تبدیل های ابتدایی) که شامل استفاده از روش گاوس یا روش گاوس-جردن است، در قسمت دوم بررسی می شود.

روش ماتریس الحاقی (اتحادیه).

اجازه دهید ماتریس $A_(n\times n)$ داده شود. برای یافتن ماتریس معکوس $A^(-1)$، سه مرحله مورد نیاز است:

1. تعیین کننده ماتریس $A$ را پیدا کنید و مطمئن شوید که $\Delta A\neq 0$، یعنی. که ماتریس A غیر دژنره است.
2. مکمل های جبری $A_(ij)$ از هر عنصر ماتریس $A$ را بنویسید و ماتریس $A_(n\times n)^(*)=\left(A_(ij) \راست)$ را از قسمت پیدا شده یادداشت کنید. مکمل های جبری
3. ماتریس معکوس را با در نظر گرفتن فرمول $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$ بنویسید.

ماتریس $(A^(*))^T$ اغلب به عنوان ماتریس الحاقی (متقابل، متحد) $A$ نامیده می شود.

اگر تصمیم به صورت دستی گرفته شود، روش اول فقط برای ماتریس های سفارشات نسبتا کوچک خوب است: دوم ()، سوم ()، چهارم (). برای یافتن ماتریس معکوس برای یک ماتریس مرتبه بالاتر، از روش های دیگری استفاده می شود. برای مثال روش گاوس که در قسمت دوم به آن پرداخته شده است.

مثال شماره 1

پیدا کردن ماتریس معکوس به ماتریس $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(آرایه) \راست)$.

از آنجایی که تمام عناصر ستون چهارم برابر با صفر هستند، پس $\Delta A=0$ (یعنی ماتریس $A$ منحط است). از آنجایی که $\Delta A=0$، هیچ ماتریسی معکوس به $A$ وجود ندارد.

پاسخ: ماتریس $A^(-1)$ وجود ندارد.

مثال شماره 2

ماتریس معکوس ماتریس $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$ را پیدا کنید. یک چک اجرا کنید.

ما از روش ماتریس الحاقی استفاده می کنیم. ابتدا، بیایید تعیین کننده ماتریس داده شده $A$ را پیدا کنیم:

$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

از آنجایی که $\Delta A \neq 0$ است، پس ماتریس معکوس وجود دارد، بنابراین راه حل را ادامه می دهیم. یافتن مکمل های جبری

\begin(تراز شده) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(تراز شده)

ماتریسی از متمم های جبری بسازید: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

ماتریس حاصل را جابجا کنید: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (نتیجه ماتریس اغلب ماتریس الحاقی یا اتحادی به ماتریس $A$ نامیده می شود. با استفاده از فرمول $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$، داریم:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

بنابراین ماتریس معکوس پیدا می شود: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \ راست) $. برای بررسی صحت نتیجه کافی است صحت یکی از برابری ها را بررسی کنید: $A^(-1)\cdot A=E$ یا $A\cdot A^(-1)=E$. بیایید برابری $A^(-1)\cdot A=E$ را بررسی کنیم. برای اینکه کمتر با کسرها کار کنیم، ماتریس $A^(-1)$ را جایگزین می کنیم نه به شکل $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ اما بصورت $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \ end(array )\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( آرایه)\راست)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array )\راست) =E $$

پاسخ: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

مثال شماره 3

معکوس ماتریس $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$ را پیدا کنید. یک چک اجرا کنید.

بیایید با محاسبه تعیین کننده ماتریس $A$ شروع کنیم. بنابراین، تعیین کننده ماتریس $A$ است:

$$ \Delta A=\left| \begin(array) (cccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \\right| = 18-36+56-12=26. $$

از آنجایی که $\Delta A\neq 0$ است، پس ماتریس معکوس وجود دارد، بنابراین راه حل را ادامه می دهیم. ما مکمل های جبری هر عنصر از ماتریس داده شده را پیدا می کنیم:

$$ \begin(تراز شده) & A_(11)=(-1)^(2)\cdot\left|\begin(array)(cc) 9 & 4\\ 3 & 2\end(array)\right| =6;\; A_(12)=(-1)^(3)\cdot\left|\begin(array)(cc) -4 &4 \\ 0 & 2\end(array)\right|=8;\; A_(13)=(-1)^(4)\cdot\left|\begin(array)(cc) -4 & 9\\ 0 & 3\end(array)\right|=-12;\\ & A_(21)=(-1)^(3)\cdot\left|\begin(array)(cc) 7 & 3\\ 3 & 2\end(array)\right|=-5;\; A_(22)=(-1)^(4)\cdot\left|\begin(array)(cc) 1 & 3\\ 0 & 2\end(array)\right|=2;\; A_(23)=(-1)^(5)\cdot\left|\begin(array)(cc) 1 & 7\\ 0 & 3\end(array)\right|=-3;\\ & A_ (31)=(-1)^(4)\cdot\left|\begin(array)(cc) 7 & 3\\ 9 & 4\end(array)\right|=1;\; A_(32)=(-1)^(5)\cdot\left|\begin(array)(cc) 1 & 3\\ -4 & 4\end(array)\right|=-16;\; A_(33)=(-1)^(6)\cdot\left|\begin(array)(cc) 1 & 7\\ -4 & 9\end(array)\right|=37. \end (تراز شده) $$

ماتریسی از اضافات جبری می سازیم و آن را جابجا می کنیم:

$$ A^*=\left(\begin(array) (cccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \راست) . $$

با استفاده از فرمول $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$، دریافت می کنیم:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(آرایه) \راست) $$

بنابراین $A^(-1)=\left(\begin(array) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. برای بررسی صحت نتیجه کافی است صحت یکی از برابری ها را بررسی کنید: $A^(-1)\cdot A=E$ یا $A\cdot A^(-1)=E$. بیایید برابری $A\cdot A^(-1)=E$ را بررسی کنیم. برای اینکه کمتر با کسرها کار کنیم، ماتریس $A^(-1)$ را جایگزین می کنیم نه به شکل $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$، اما به صورت $\frac(1)(26)\ cdot \left( \begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(cccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end (array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (cccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(آرایه) \راست) =\frac(1)(26)\cdot\left(\begin(array) (cccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\ end (آرایه) \راست) =\ چپ (\شروع (آرایه) (cccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end (آرایه) \راست) =E $$

چک با موفقیت پاس شد، ماتریس معکوس $A^(-1)$ به درستی یافت شد.

پاسخ: $A^(-1)=\left(\begin(array) (cccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

مثال شماره 4

ماتریس معکوس $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 را پیدا کنید & -8 & -3 \end(array) \right)$.

برای ماتریس مرتبه چهارم، یافتن ماتریس معکوس با استفاده از اضافات جبری تا حدودی دشوار است. با این حال، چنین نمونه هایی در کارهای کنترلی یافت می شود.

برای پیدا کردن ماتریس معکوس، ابتدا باید تعیین کننده ماتریس $A$ را محاسبه کنید. بهترین راه برای انجام این کار در این شرایط، گسترش دترمینان در یک ردیف (ستون) است. هر سطر یا ستونی را انتخاب می کنیم و مکمل جبری هر عنصر سطر یا ستون انتخاب شده را پیدا می کنیم.

به عنوان مثال، برای ردیف اول دریافت می کنیم:

$$ A_(11)=\left|\begin(array)(cccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(array)(cccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\چپ|\begin(array)(cccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\left|\begin(array)(cccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

تعیین کننده ماتریس $A$ با فرمول زیر محاسبه می شود:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14 )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(تراز شده) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end (تراز شده) $$

ماتریس متمم جبری: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(آرایه)\راست)$.

ماتریس پیوست: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(آرایه)\راست)$.

ماتریس معکوس:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 و 1/25 و 9/25 و -24/25 \end(آرایه) \راست) $$

بررسی در صورت تمایل می تواند مانند نمونه های قبلی انجام شود.

پاسخ: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(آرایه) \راست) $.

در بخش دوم راه دیگری برای یافتن ماتریس معکوس در نظر گرفته می شود که شامل استفاده از تبدیل های روش گاوس یا روش گاوس-جردن است.

اضافات جبری و صغیر

بیایید یک تعیین کننده مرتبه سوم داشته باشیم: .

جزئیمربوط به این عنصر aijدترمینان مرتبه سوم به دترمینان مرتبه دوم گفته می شود که با حذف سطر و ستونی که در محل تقاطع آنها عنصر داده شده قرار دارد، به دست می آید. من-خط و jستون -ام. مینورهای مربوط به یک عنصر معین aijنشان خواهیم داد M ij.

مثلا، جزئی M12مربوط به عنصر یک 12، یک تعیین کننده وجود خواهد داشت 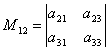که با حذف سطر 1 و ستون 2 از دترمینان داده شده به دست می آید.

بنابراین، فرمولی که تعیین کننده مرتبه سوم را تعیین می کند نشان می دهد که این تعیین کننده برابر است با مجموع حاصل ضرب عناصر ردیف 1 و جزئی های مربوط به آنها. در حالی که جزئی مربوط به عنصر یک 12، با علامت "-" گرفته می شود، یعنی. می توان نوشت که

.

(1)

به همین ترتیب، می توان تعاریفی از صغیر را برای تعیین کننده های مرتبه دوم و بالاتر ارائه کرد.

بیایید یک مفهوم دیگر را معرفی کنیم.

جمع جبریعنصر aijتعیین کننده جزئی آن نامیده می شود M ijضرب در (–1) i+j .

جمع عنصر جبری aijنشان داده شده است یک ij.

از تعریف دریافت می کنیم که ارتباط بین متمم جبری یک عنصر و جزئی آن با برابری بیان می شود. یک ij= (–1) i+j M ij.

مثلا،

مثال.با توجه به یک عامل تعیین کننده. برای پیدا کردن A 13، A 21، A 32.

به راحتی می توان دریافت که با استفاده از جمع جبری عناصر، فرمول (1) را می توان به صورت زیر نوشت:

مشابه این فرمول، می توان تجزیه دترمینان را بر روی عناصر هر سطر یا ستون بدست آورد.

به عنوان مثال، تجزیه دترمینان بر روی عناصر ردیف 2 را می توان به صورت زیر بدست آورد. با توجه به خاصیت 2 تعیین کننده داریم:

بیایید تعیین کننده به دست آمده را با عناصر ردیف 1 گسترش دهیم.

.

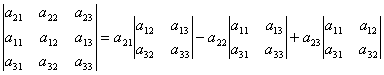(2)

از اینجا زیرا تعیین کننده های مرتبه دوم در فرمول (2) جزئی عناصر هستند a 21، a 22، a 23. بنابراین، یعنی ما بسط دترمینان را با عناصر ردیف 2 به دست آورده ایم.

به طور مشابه، می توان تجزیه دترمینان را بر روی عناصر ردیف سوم بدست آورد. با استفاده از ویژگی 1 تعیین کننده ها (در جابجایی)، می توان نشان داد که بسط های مشابه برای بسط در عناصر ستون نیز معتبر هستند.

بنابراین، قضیه زیر درست است.

قضیه (در مورد بسط دترمینان در یک سطر یا ستون معین).تعیین کننده برابر است با مجموع حاصل ضرب عناصر هر یک از سطرها (یا ستون ها) و مکمل های جبری آنها.

تمام موارد فوق برای تعیین کننده های هر مرتبه بالاتر صادق است.

مثال ها.

ماتریس معکوس

مفهوم ماتریس معکوس فقط برای معرفی شده است ماتریس های مربع.

اگر یک آپس یک ماتریس مربع است معکوسبرای آن، یک ماتریس یک ماتریس است که نشان داده شده است الف-1و ارضای شرط . (این تعریف با قیاس با ضرب اعداد ارائه شده است)