Розглянемо криволінійну трапецію, обмежену віссю Ох, кривої y \u003d f (x) і двома прямими: х \u003d а і х \u003d Ь (рис. 85). Візьмемо довільне значення х (тільки не а й не Ь). Дамо йому приріст h \u003d dx і розглянемо смужку, обмежену прямими АВ і CD, віссю Ох і дугою BD, що належить даної кривої. Цю смужку будемо називати елементарною смужкою. Площа елементарної смужки відрізняється від площі прямокутника ACQB на криволінійний трикутник BQD, а площа останнього менше площі прямокутника BQDM зі сторонами BQ \u003d \u003d h \u003d dx) QD \u003d Ay і площею, яка дорівнює hAy \u003d Ay dx. Зі зменшенням боку h сторона Ду також зменшується і одночасно з h прагне до нуля. Тому площа BQDM є нескінченно малою другого порядку. Площа елементарної смужки є приріст площі, а площа прямокутника ACQB, рівна АВ-АС \u003d\u003d / (х) dx\u003e є диференціал площі. Отже, саму площу знайдемо, інтегруючи її диференціал. В межах даної фігури незалежне змінне л: змінюється від а до b, тому шукана площа 5 буде дорівнює 5 \u003d \\ f (x) dx. (I) Приклад 1. Обчислимо площу, обмежену параболою у - 1 х *, прямими X \u003d - Fj-, х \u003d 1 і віссю О * (рис. 86). у Рис. 87. Рис. 86. 1 Тут f (x) \u003d 1 - л ?, межі інтегрування а \u003d - і £ \u003d 1, тому J [* -т] \\ - -fl - Г -1- ± Л_ 1V1 -ll-Ii- ^ 3) | _ 2 3V 2 / J 3 24 24 * Приклад 2. Обчислимо площу, обмежену синусоїдою y \u003d sinXy віссю Ох і прямий (рис. 87). Застосовуючи формулу (I), отримуємо Л 2 S \u003d J sinxdx \u003d [-cos x] Q \u003d 0 - (- 1) \u003d lf Приклад 3. Обчислимо площу, обмежену дугою синусоїди ^ у \u003d sin jc, укладеної між двома сусідніми точками перетину з віссю Ох (наприклад, між початком координат і точкою з абсцисою я). Зауважимо, що з геометричних міркувань ясно, що ця площа буде в два рази більше площі попереднього прикладу. Однак виконаємо обчислення: я 5 \u003d | s \\ nxdx \u003d [- cosх) * - - cos я - (- cos 0) \u003d 1 + 1 \u003d 2. про Дійсно, наше припущення виявилося справедливим. Приклад 4. Обчислити площу, обмежену синусоїдою і ^ віссю Ох на одному пе-х періоді (рис. 88). Попередні рас-рис судження дозволяють припустити, що площа вийде в чотири рази більше, ніж в ін. 2. Однак, провівши обчислення, отримаємо «я Г, * я S - \\ sin х dx \u003d [- cos х] 0 \u003d \u003d - cos 2л - (- cos 0) \u003d - 1 + 1 \u003d 0. Цей результат вимагає роз'яснень. Для з'ясування суті справи обчислюємо ще площа, обмежену тієї ж синусоїдою у \u003d sin л: і віссю Ох в межах від л до 2га. Застосовуючи формулу (I), отримуємо 2л $ 2л sin хdx \u003d [- cosх] л \u003d -cos 2а ~) -с05я \u003d - 1-1 \u003d -2. я Таким чином, бачимо, що ця площа вийшла негативною. Порівнюючи її з площею, обчисленої в ін. 3, отримуємо, що їх абсолютні величини однакові, а знаки різні. Якщо застосувати властивість V (див. Гл. XI, § 4), то отримаємо 2л я 2л J sin xdx \u003d J sin * dx [sin x dx \u003d 2 + (- 2) \u003d 0То, що вийшло в цьому прикладі, не є випадковістю. Завжди площа, розташована нижче осі Ох, за умови, що незалежне змінне змінюється зліва направо, виходить при обчисленні за допомогою інтегралів негативною. У цьому курсі ми завжди будемо розглядати площі без знаків. Тому відповідь у щойно розібраному прикладі буде таким: шукана площа дорівнює 2 + | -2 | \u003d 4. Приклад 5. Обчислимо площу ОАВ, зазначену на рис. 89. Ця площа обмежена віссю Ох, параболою у \u003d - ХГ і прямий у - \u003d х + \\. Площа криволінійної трапеції Шукана площа ОАВ складається з двох частин: ОАМ і МАВ. Так як точка А є точкою перетину параболи і прямої, то її координати знайдемо, вирішуючи систему рівнянь 3 2 У \u003d тх. (Нам потрібно знайти тільки абсциссу точки А). Вирішуючи систему, знаходимо л; \u003d ~. Тому площа доводиться обчислювати по частинах, спочатку пл. ОАМ, а потім пл. МАВ: .... Г 3 2, 3 Г ХП 3 1/2 У 2. QAM- ^ х і не змінює на ньому свій знак (Рис. 1).Площа криволінійної трапеції можна позначити S (G).

Певний інтеграл ʃ а b f (x) dx для функції f (x), що є безперервною і неотрицательной на відрізку [а; b], і є площа відповідної криволінійної трапеції.

Тобто, щоб знайти площу фігури G, обмеженої лініями y \u003d f (x), у \u003d 0, х \u003d а і х \u003d b, необхідно обчислити визначений інтеграл ʃ а b f (x) dx.

Таким чином, S (G) \u003d ʃ а b f (x) dx.

У разі, якщо функція y \u003d f (x) не позитивний на [а; b], то площа криволінійної трапеції може бути знайдена за формулою S (G) \u003d -ʃ а b f (x) dx.

Приклад 1.

Обчислити площу фігури, обмеженої лініями у \u003d х 3; у \u003d 1; х \u003d 2.

Рішення.

Задані лінії утворюють фігуру АВС, яка показана штрихуванням на рис. 2.

Шукана площа дорівнює різниці між площами криволінійної трапеції DACE і квадрата DABE.

Використовуючи формулу S \u003d ʃ а b f (x) dx \u003d S (b) - S (a), знайдемо межі інтегрування. Для цього вирішимо систему двох рівнянь:

(У \u003d х 3,
(У \u003d 1.

Таким чином, маємо х 1 \u003d 1 - нижня межа і х \u003d 2 - верхня межа.

Отже, S \u003d S DACE - S DABE \u003d ʃ 1 2 x 3 dx - 1 \u003d x 4/4 | 1 2 - 1 \u003d (16 - 1) / 4 - 1 \u003d 11/4 (кв. Од.).

Відповідь: 11/4 кв. од.

Приклад 2.

Обчислити площу фігури, обмеженої лініями у \u003d √х; у \u003d 2; х \u003d 9.

Рішення.

Задані лінії утворюють фігуру АВС, яка обмежена зверху графіком функції

у \u003d √х, а знизу графіком функції у \u003d 2. Отримана фігура показана штрихуванням на рис. 3.

Шукана площа дорівнює S \u003d ʃ а b (√x - 2). Знайдемо межі інтегрування: b \u003d 9, для знаходження а, вирішимо систему двох рівнянь:

(У \u003d √х,
(У \u003d 2.

Таким чином, маємо, що х \u003d 4 \u003d а - це нижня межа.

Отже, S \u003d ∫ 4 9 (√x - 2) dx \u003d ∫ 4 9 √x dx -∫ 4 9 2dx \u003d 2/3 x√х | 4 9 - 2х | 4 9 \u003d (18 - 16/3) - (18 - 8) \u003d 2 2/3 (кв. Од.).

Відповідь: S \u003d 2 2/3 кв. од.

Приклад 3.

Обчислити площу фігури, обмеженої лініями у \u003d х 3 - 4х; у \u003d 0; х ≥ 0.

Рішення.

Побудуємо графік функції у \u003d х 3 - 4х при х ≥ 0. Для цього знайдемо похідну у ':

y '\u003d 3x 2 - 4, y' \u003d 0 при х \u003d ± 2 / √3 ≈ 1,1 - критичні точки.

Якщо зобразити критичні точки на числовій осі і розставити знаки похідної, то отримаємо, що функція спадає від нуля до 2 / √3 і зростає від 2 / √3 до плюс нескінченності. Тоді х \u003d 2 / √3 - точка мінімуму, мінімальне значення функції у min \u003d -16 / (3√3) ≈ -3.

Визначимо точки перетину графіка з осями координат:

якщо х \u003d 0, то у \u003d 0, а значить, А (0; 0) - точка перетину з віссю Оу;

якщо у \u003d 0, то х 3 - 4х \u003d 0 або х (х 2 - 4) \u003d 0, або х (х - 2) (х + 2) \u003d 0, звідки х 1 \u003d 0, х 2 \u003d 2, х 3 \u003d -2 (не підходить, тому що х ≥ 0).

Точки А (0; 0) і В (2; 0) - точки перетину графіка з віссю Ох.

Задані лінії утворюють фігуру ОАВ, яка показана штрихуванням на рис. 4.

Так як функція у \u003d х 3 - 4х приймає на (0; 2) від'ємне значення, то

S \u003d | ʃ 0 2 (x 3 - 4x) dx |.

Маємо: ʃ 0 2 (x 3 - 4х) dx \u003d (x 4/4 - 4х 2/2) | 0 2 \u003d -4, звідки S \u003d \u200b\u200b4 кв. од.

Відповідь: S \u003d 4 кв. од.

Приклад 4.

Знайти площу фігури, обмеженою параболою у \u003d 2х 2 - 2х + 1, прямими х \u003d 0, у \u003d 0 і дотичній до даної параболі в точці з абсцисою х 0 \u003d 2.

Рішення.

Спочатку складемо рівняння дотичної до параболи у \u003d 2х 2 - 2х + 1 в точці з абсцисою х₀ \u003d 2.

Так як похідна y '\u003d 4x - 2, то при х 0 \u003d 2 отримаємо k \u003d y' (2) \u003d 6.

Знайдемо ординату точки дотику: у 0 \u003d 2 · 2 2 - 2 · 2 + 1 \u003d 5.

Отже, рівняння дотичної має вигляд: у - 5 \u003d 6 (х - 2) або у \u003d 6х - 7.

Побудуємо фігуру, обмежену лініями:

у \u003d 2х 2 - 2х + 1, у \u003d 0, х \u003d 0, у \u003d 6х - 7.

Г у \u003d 2х 2 - 2х + 1 - парабола. Точки перетину з осями координат: А (0; 1) - з віссю Оу; з віссю Ох - немає точок перетину, тому що рівняння 2х 2 - 2х + 1 \u003d 0 не має рішень (D< 0). Найдем вершину параболы:

x b \u003d 2/4 \u003d 1/2;

y b \u003d 1/2, тобто вершина параболи точка В має координати В (1/2; 1/2).

Отже, фігура, площа якої потрібно визначити, показана штрихуванням на рис. 5.

Маємо: S Про A В D \u003d S OABC - S ADBC.

Знайдемо координати точки D з умови:

6х - 7 \u003d 0, тобто х \u003d 7/6, значить DC \u003d 2 - 7/6 \u003d 5/6.

Площа трикутника DBC знайдемо за формулою S ADBC \u200b\u200b\u003d 1/2 · DC · BC. Таким чином,

S ADBC \u200b\u200b\u003d 1/2 · 5/6 · 5 \u003d 25/12 кв. од.

S OABC \u003d ʃ 0 2 (2x 2 - 2х + 1) dx \u003d (2x 3/3 - 2х 2/2 + х) | 0 2 \u003d 10/3 (кв. Од.).

Остаточно отримаємо: S Про A В D \u003d S OABC - S ADBC \u200b\u200b\u003d 10/3 - 25/12 \u003d 5/4 \u003d 1 1/4 (кв. Од).

Відповідь: S \u003d 1 1/4 кв. од.

Ми розібрали приклади знаходження площ фігур, обмежених заданими лініями. Для успішного вирішення подібних завдань потрібно вміти будувати на площині лінії і графіки функцій, знаходити точки перетину ліній, застосовувати формулу для знаходження площі, що має на увазі наявність умінь і навичок обчислення певних інтегралів.

сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.

У будь-якого певного інтеграла (який існує) є дуже хороший геометричний сенс. На уроці я говорив, що визначений інтеграл - це число. А зараз прийшла пора констатувати ще один корисний факт. З точки зору геометрії визначений інтеграл - це ПЛОЩА.

Тобто, певного інтеграла (якщо він існує) геометрично відповідає площа деякої фігури. Наприклад, розглянемо певний інтеграл. Підінтегральна функція задає на площині деяку криву (її можна завжди при бажанні накреслити), а сам певний інтеграл чисельно дорівнює площі відповідної криволінійної трапеції.

приклад 1

Це типова формулювання завдання. Перший і найважливіший момент рішення - побудова креслення. Причому, креслення необхідно побудувати ПРАВИЛЬНО.

При побудові креслення я рекомендую наступний порядок: спочатку краще побудувати всі прямі (якщо вони є) і тільки потім - параболи, гіперболи, графіки інших функцій. Графіки функцій вигідніше будувати поточечно, З технікою поточечного побудови можна ознайомитися в довідковому матеріалі.

Там же можна знайти дуже корисний стосовно нашого уроку матеріал - як швидко побудувати параболу.

У цьому завданню рішення може виглядати так.
Виконаємо креслення (зверніть увагу, що рівняння задає вісь):

Штрихована криволинейную трапецію я не буду, тут очевидно, про яку площі йдеться. Рішення триває так:

На відрізку графік функції розташований над віссю, Тому:

відповідь:

У кого виникли труднощі з обчисленням певного інтеграла і застосуванням формули Ньютона-Лейбніца , Зверніться до лекції Визначений інтеграл. приклади рішень.

Після того, як завдання виконано, завжди корисно поглянути на креслення і прикинути, чи реальний вийшов відповідь. В даному випадку «на око» підраховуємо кількість клітинок в кресленні - ну, приблизно 9 набереться, схоже на правду. Цілком зрозуміло, що якби у нас вийшов, скажімо, відповідь: 20 квадратних одиниць, то, очевидно, що десь допущена помилка - в розглянуту фігуру 20 клітинок явно не вміщається, від сили десяток. Якщо відповідь вийшов негативним, то завдання теж вирішено некоректно.

приклад 2

Обчислити площу фігури, обмеженої лініями,, і віссю

Це приклад для самостійного рішення. Повне рішення і відповідь в кінці уроку.

Що робити, якщо криволинейная трапеція розташована під віссю?

приклад 3

Обчислити площу фігури, обмеженої лініями, і координатними осями.

Рішення: Виконаємо креслення:

Якщо криволінійна трапеція повністю розташована під віссю, То її площа можна знайти за формулою:
В даному випадку:

Увага! Не слід плутати два типи завдань:

1) Якщо Вам запропоновано вирішити просто певний інтеграл без всякого геометричного сенсу, то він може бути негативним.

2) Якщо Вам запропоновано знайти площу фігури за допомогою певного інтеграла, то площа завжди позитивна! Саме тому в тільки що розглянутої формулою фігурує мінус.

На практиці найчастіше фігура розташована і в верхній і в нижній півплощині, а тому, від найпростіших шкільних задачок переходимо до більш змістовним прикладів.

приклад 4

Знайти площу плоскої фігури, обмеженої лініями,.

Рішення: Спочатку потрібно виконати креслення. Взагалі кажучи, при побудові креслення в задачах на площу нас найбільше цікавлять точки перетину ліній. Знайдемо точки перетину параболи і прямої. Це можна зробити двома способами. Перший спосіб - аналітичний. Вирішуємо рівняння:

Значить, нижня межа інтегрування, верхня межа інтегрування.
Цим способом краще, по можливості, не користуватися.

Набагато вигідніше і швидше побудувати лінії поточечно, при цьому межі інтегрування з'ясовуються як би «самі собою». Техніка поточечного побудови для різних графіків докладно розглянута в довідці Графіки і властивості елементарних функцій. Проте, аналітичний спосіб знаходження меж все-таки доводиться іноді застосовувати, якщо, наприклад, графік досить великий, або поточені побудова не виявило меж інтегрування (вони можуть бути дробовими або ірраціональними). І такий приклад, ми теж розглянемо.

Повертаємося до нашого завдання: раціональніше спочатку побудувати пряму і тільки потім параболу. Виконаємо креслення:

Повторюся, що при поточечной побудові межі інтегрування найчастіше з'ясовуються «автоматом».

А тепер робоча формула: Якщо на відрізку деяка безперервна функція більше або дорівнює деякої неперервної функції, то площа відповідної фігури можна знайти за формулою:

Тут вже не треба думати, де розташована фігура - над віссю або під віссю, і, грубо кажучи, важливо, який графік ВИЩЕ(Щодо іншого графіка), а який - НИЖЧЕ.

У розглянутому прикладі очевидно, що на відрізку парабола розташовується вище прямої, а тому з необхідно відняти

Завершення рішення може виглядати так:

Шукана фігура обмежена параболою зверху і прямий знизу.
На відрізку, за відповідною формулою:

відповідь:

Насправді шкільна формула для площі криволінійної трапеції в нижній півплощині (див. Простенький приклад №3) - окремий випадок формули . Оскільки вісь задається рівнянням, а графік функції розташований нижче осі, то

А зараз кілька прикладів для самостійного рішення

приклад 5

приклад 6

Знайти площу фігури, обмеженої лініями,.

В ході вирішення задач на обчислення площі за допомогою визначеного інтеграла іноді трапляється кумедний казус. Креслення виконано правильно, розрахунки - правильно, але через неуважність ... знайдена площа не тієї фігури, Саме так кілька разів лажа ваш покірний слуга. Ось реальний випадок з життя:

приклад 7

Обчислити площу фігури, обмеженої лініями,,,.

Спочатку виконаємо креслення:

Фігура, площа якої нам потрібно знайти, заштрихована синім кольором(Уважно дивіться на умова - чим обмежена фігура!). Але на практиці через неуважність нерідко виникає, що потрібно знайти площу фігури, яка заштрихована зеленим кольором!

Цей приклад ще й корисний тим, що в ньому площу фігури вважається за допомогою двох визначених інтегралів. дійсно:

1) На відрізку над віссю розташований графік прямої;

2) На відрізку над віссю розташований графік гіперболи.

Цілком очевидно, що площі можна (і потрібно) приплюсувати, тому:

відповідь:

приклад 8

Обчислити площу фігури, обмеженої лініями,
Уявімо рівняння в «шкільному» вигляді, і виконаємо поточечной креслення:

З креслення видно, що верхня межа у нас «хороший»:.
Але чому дорівнює нижня межа ?! Зрозуміло, що це не ціле число, але яке? Може бути ? Але де гарантія, що креслення виконаний з ідеальною точністю, цілком може виявитися що. Або корінь. А якщо ми взагалі неправильно побудували графік?

У таких випадках доводиться витрачати додатковий час і уточнювати межі інтегрування аналітично.

Знайдемо точки перетину прямої і параболи.
Для цього вирішуємо рівняння:

Отже,.

Подальше рішення тривіально, головне, не заплутатися в підстановках і знаках, обчислення тут не найпростіші.

на відрізку , За відповідною формулою:

відповідь:

Ну, і на закінчення уроку, розглянемо два завдання складніше.

приклад 9

Обчислити площу фігури, обмеженої лініями,,

Рішення: Зобразимо цю фігуру на кресленні.

Для поточечного побудови креслення необхідно знати зовнішній вигляд синусоїди (і взагалі корисно знати графіки всіх елементарних функцій), А також деякі значення синуса, їх можна знайти в тригонометричної таблиці. У ряді випадків (як в цьому) допускається побудова схематичного креслення, на якому принципово правильно повинні бути відображені графіки і межі інтегрування.

З межами інтегрування тут проблем немає, вони йдуть прямо з умови: - «ікс» змінюється від нуля до «пі». Оформляємо подальше рішення:

На відрізку графік функції розташований над віссю, тому:

(1) Як інтегруються синуси і косинуси в непарних ступенях можна подивитися на уроці Інтеграли від тригонометричних функцій. Це типовий прийом, відщипуємо один синус.

(2) Використовуємо основне тригонометричну тотожність у вигляді

(3) Проведемо заміну змінної, тоді:

Нові переділи інтегрування:

У кого зовсім погані справи з замінами, прошу пройти на урок Метод заміни в невизначеному інтегралі. Кому не дуже зрозумілий алгоритм заміни в певному інтегралі, відвідайте сторінку Визначений інтеграл. приклади рішень.

Вступ

Знаходження похідної f "(x) або диференціала df \u003d f" (x) dx функції f (x) є основним завданням диференціального обчислення. В інтегральному численні вирішується зворотна задача: по заданій функції f (x) потрібно знайти таку функцію F (x), що F "(х) \u003d f (x) або F (x) \u003d F" (x) dx \u003d f (x ) dx. Таким чином, основним завданням інтегрального числення є відновлення функції F (x) за відомою похідною (диференціалу) цієї функції. Інтегральне числення має численні застосування в геометрії, механіці, фізиці і техніці. Воно дає загальний метод знаходження площ, обсягів, центрів тяжіння і т.д.

Курс математичного аналізу містить різноманітний матеріал, проте, одним з його центральних розділів є певний інтеграл. Інтегрування багатьох видів функцій часом є однією з найважчих проблем математичного аналізу.

Обчислення визначеного інтеграла має не тільки теоретичний інтерес. До його обчислення зводяться іноді завдання, пов'язані з практичною діяльністю людини.

Також поняття певного інтеграла широко використовується у фізиці.

Знаходження площі криволінійної трапеції

Криволінійної трапецією називається фігура, розташована в прямокутній системі координат і обмежена віссю абсцис, прямими х \u003d а і х \u003d b і кривої, причому неотрицательна на відрізку. Наближено площа криволінійної трапеції можна знайти так:

1. розділити відрізок осі абсцис на n рівних відрізків;

2. провести через точки поділу відрізки, перпендикулярні до осі абсцис, до перетину з кривою;

3. замінити отримані стовпчики прямокутниками з основою і висотою, що дорівнює значенню функції f в лівому кінці кожного відрізка;

4. Визначити суму площ цих прямокутників.

Але можна знайти площу криволінійної інакше: за формулою Ньютона-Лейбніца. Для доказу формули, що носить їх імена, доведемо, що площа криволінійної трапеції дорівнює, де - будь-яка з первісних функції, графік якої обмежує криволінійну трапецію.

Обчислення площі криволінійної трапеції записується так:

1. знаходиться будь-яка з первісних функції.

2. записується. - це формула Ньютона-Лейбніца.

Знаходження площі криволінійного сектора

Розглянемо криву? \u003d? (?) В полярній системі координат, де? (?) - безперервна і неотрицательная на [?; ?] Функція. Фігура, обмежена кривою? (?) І променями? \u003d?,? \u003d?, Називається криволінійним сектором. Площа криволінійного сектора дорівнює

Знаходження довжини дуги кривої

прямокутні координати

Нехай в прямокутних координатах дана плоска крива AB, рівняння якої y \u003d f (x), де a? x? b. (Рис 2)

Під довжиною дуги AB розуміється межа, до якого прагнути довжина ламаної лінії, вписаної в цю дугу, коли число ланок ламаної необмежено зростає, а довжина найбільшого ланки її прагнути до нуля.

Застосуємо схему I (метод сум).

Точками X \u003d a, X, ..., X \u003d b (X? X? ...? X) розіб'ємо відрізок на n частин. Нехай цим точкам відповідають точки M \u003d A, M, ..., M \u003d B на кривій AB. Проведемо хорди MM, MM, ..., MM, довжини яких позначимо відповідно через? L,? L, ...,? L.

Отримаємо ламану MMM ... MM, довжина якої дорівнює L \u003d? L +? L + ... +? L \u003d? L.

Довжину хорди (або ланки ламаної)? L можна знайти по теоремі Піфагора з трикутника з катетами? X і? Y:

L \u003d, де? X \u003d X - X,? Y \u003d f (X) - f (X).

По теоремі Лагранжа про кінцевий збільшенні функції

Y \u003d (C)? X, де C (X, X).

а довжина всієї ламаної MMM ... MM дорівнює

Довжина кривої AB, за визначенням, дорівнює

Зауважимо, що при? L 0 також і? X 0 (? L \u003d і отже |? X |< ?L). Функция непрерывна на отрезке , так как, по условию, непрерывна функция f (X). Следовательно, существует предел интегральной суммы L=?L= , кода max ?X 0:

Таким чином, L \u003d dx.

Приклад: Знайти довжину кола радіуса R. (рис 3)

Знайдемо? частина її довжини від точки (0; R) до точки (R; 0). Так як

№ ____ Дата ________

Тема:Криволінійна трапеція і її май ь

Мета уроку: Дати визначення криволінійної трапеції і її площі, навчитися обчислювати площу криволінійної трапеції.

ХІД УРОКУ

1. Організаційний момент.

Привітання учнів, перевірка готовності класу до уроку, організація уваги учнів, розкриття загальних цілей уроку і плану його проведення.

2. Етап перевірки домашнього завдання.

Завдання: Встановити правильність, повноту і усвідомленість виконання д / з усіма учнями, виявити прогалини в знаннях і способах діяльності учнів. Визначити причини виникнення труднощів, усунути виявлені прогалини.

3.Етапи актуалізації.

Завдання: забезпечення мотивації навчання школярів, включення в спільну діяльність з визначення цілей уроку. Актуалізувати суб'єктивний досвід учнів.

Згадаймо основні поняття і формули.

Визначення. функція y \u003df(X), x (A, b), називається первісною для функції y \u003d f (x), x (A, b), якщо для кожного x (A, b) виконується рівність

F (X) \u003d f (x).

Зауваження. якщо f(X) є первісна для функції f (x), То при будь-константі З, F (x) + C також є первісною для f (x).

Завдання знаходження всіх первісних функції f (x) називається інтегруванням, а безліч всіх первісних називається невизначеним інтегралом для функції f (x) по dx і позначається

Мають місце властивості:

1. ;

2. якщо С \u003dConst, то
;

3.
.

Зауваження. У шкільному курсі математики не вживається термін «невизначений інтеграл», замість цього кажуть «безліч всіх первісних».

Наведемо таблицю невизначених інтегралів.

Приклад 1. Знайти первісну для функції
, Що проходить через точку М(2;4).

Рішення. Безліч всіх первісних функції
є невизначений інтеграл
. Обчислимо його, використовуючи властивості інтеграла 1 і 2. маємо:

Отримали, що безліч всіх первісних задається сімейством функцій y \u003d F (x) + C, тобто y \u003d x 3 – 2x + C, де З - довільна постійна.

Знаючи, що первісна проходить через точку М(2; 4), підставимо її координати в попередній вираз і знайдемо З.

4=2 3 –2 2+З  З=4–8+4; З=0.

відповідь: F (x) \u003d x 3 - 2x - шукана первісна.

4. Формування нових понять і способів дії.

Завдання: Забезпечити сприйняття, осмислення і запам'ятовування учнями досліджуваного матеріалу. Забезпечити засвоєння учнями методики відтворення вивченого матеріалу, сприяти філософського осмислення засвоюваних понять, законів, правил, формул. Встановити правильність і усвідомленість учнями вивченого матеріалу, виявити прогалини первинного осмислення, провести корекцію. Забезпечити співвіднесення учнями свого суб'єктивного досвіду з ознаками наукового знання.

Знаходження площ плоских фігур

Завдання знаходження площі плоскої фігури тісно пов'язана з завданням знаходження первісних (інтеграцією). А саме: площа криволінійної трапеції обмеженої графіком функціїy \u003d f (x) (f (x)\u003e 0) прямимиx \u003d a; x \u003d b; y \u003d 0, дорівнює різниці значень первісної для функціїy \u003d f (x) в точкахb іa :

S \u003d F (b) -F (a)

Дамо визначення певного інтеграла.

Про
пределеніе. нехай функція y \u003d f (x) визначена і інтегрована на відрізку [ a, b] і нехай F (x) - деяка її Первісна. тоді число F (b) -F (a) називається інтегралом від а до b функції f (x) і позначається

.

рівність
називається формулою Ньютона-Лейбніца.

Ця формула пов'язує завдання знаходження площі плоскої фігури з інтегралом.

У загальному випадку, якщо фігура обмежена графіками функцій y \u003d f (x); y \u003d g (x) (f (x)\u003e g (x)) І прямими x \u003d a; x \u003d b, То її площа дорівнює:

.

Приклад 2. В якій точці графіка функції y \u003d x 2 + 1 треба провести дотичну, щоб вона відтинала від фігури, утвореної графіком цієї функції і прямими y \u003d0, X \u003d0, X \u003d1 трапецію найбільшої площі?

Рішення. нехай M 0 (x 0 , y 0 ) - точка графіка функції y \u003d x 2 + 1, в якій проведена шукана дотична.

Знайдемо рівняння дотичної y \u003d y 0 + f (x 0 ) (X-x 0 ) .

маємо:

Тому

.

Знайдемо площу трапеції ОАВС.

.

B - точка перетину дотичної з прямою x \u003d1 

Завдання звелася до знаходження найбільшого значення функції

S(x)\u003d -x 2 + X +1 на відрізку. знайдемо S (x)=– 2x +1. Знайдемо критичну точку з умови S (x)= 0  x \u003d.

Бачимо, що функція досягає найбільшого значення при x \u003d. знайдемо
.

відповідь: дотичну треба провести в точці
.

Відзначимо, що часто зустрічається завдання знаходження інтеграла, виходячи з його геометричного сенсу. Покажемо на прикладі, як вирішується таке завдання.

Приклад 4. Використовуючи геометричний сенс інтеграла обчислити

а )
; б)
.

Рішення.

а)
- дорівнює площі криволінійної трапеції, обмеженою лініями.

П реобразуем

- верхня половина окружності з центром Р(1; 0) і радіусом R \u003d1.

Тому
.

відповідь: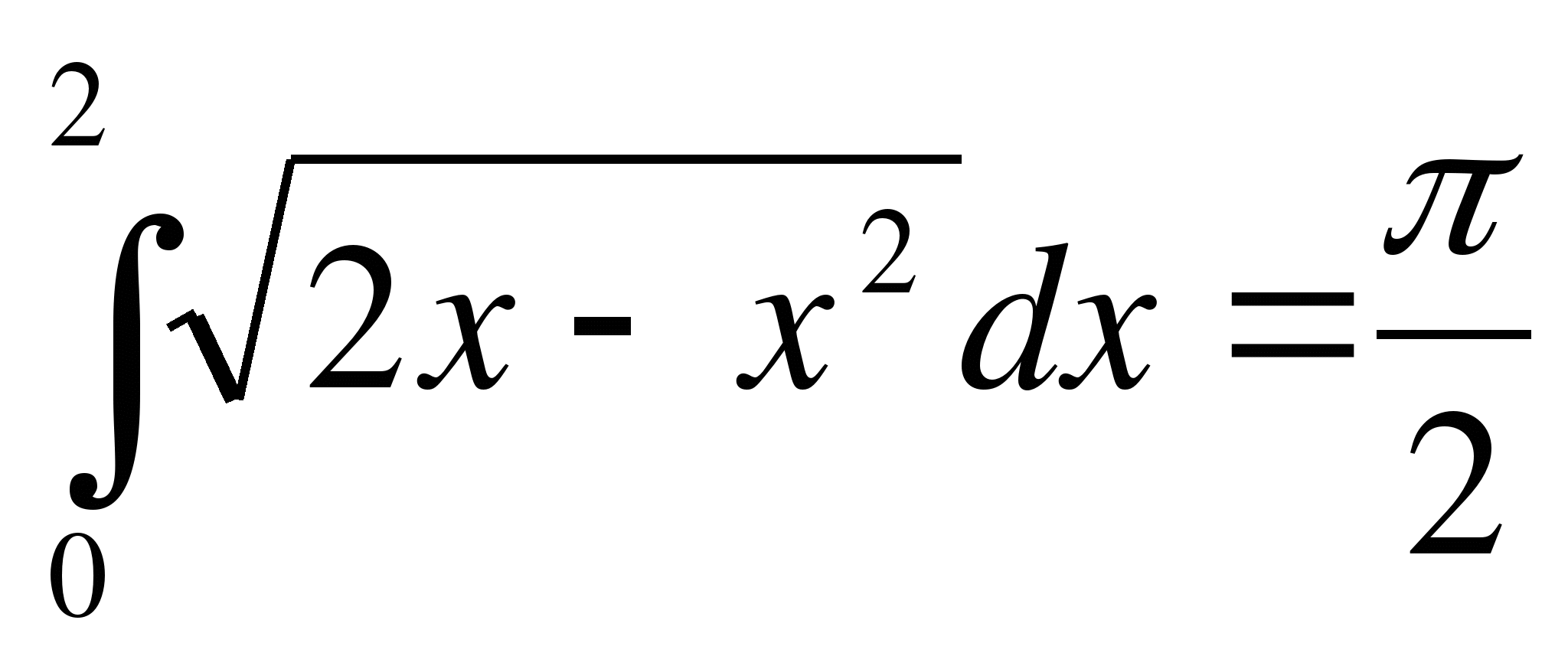
.

б) Розмірковуючи аналогічно, побудуємо область, обмежену графіками .2 – 2x +2, дотичними до неї в точках A
, B(4;2)

y \u003d–9x-59, параболою y \u003d3x 2 + Ax +1, якщо відомо, що дотична до параболи в точці x \u003d -2 становить з віссю Ox кут величиною arctg6.

знайти а, Якщо відомо, що площа криволінійної трапеції, обмеженої лініями y \u003d3x 3 + 2x, x \u003d a, y \u003d0, дорівнює одиниці.

Знайти найменше значення площі фігури, обмеженої параболою y \u003d x 2 + 2x-3 і прямий y \u003d kx +1.

6.Етап інформації про домашнє завдання.

Завдання: Забезпечити розуміння учнями мети, змісту і способів виконання домашнього заданія.№18, 19,20,21 непарні

7.Подведеніе підсумків уроку.

Завдання: Дати якісну оцінку роботи класу і окремих учнів.