Tänk på en kröktrapezion avgränsad av axeln OH, kurvan Y \u003d F (X) och två rak: X \u003d A och X \u003d B (Fig. 85). Ta det godtyckliga värdet av x (endast inte och inte b). Vi kommer att ge honom stegen h \u003d dx och överväga remsan avgränsad av rak av och cd, axelns axel och bågen BD som tillhör den aktuella kurvan. Vi kommer att ringa den här remsan med en elementärremsa. Området av den elementära remsan skiljer sig från ACQB-rektangelområdet till den kröklinjiga triangeln BQD, och området av den senare är mindre än BQDM-rektangelområdet med sidorna bq \u003d \u003d h \u003d dx) qd \u003d ay och en område lika med hö \u003d ay dx. Med en minskning av delen H minskas också sidan av fjärrkontrollen och samtidigt med H som strävar efter noll. Därför är BQDM-området en oändligt liten andra ordning. Området av elementärremsan är ökningen av området, och området för ACQB-rektangeln, lika med AV-talet \u003d\u003d / (X) DX\u003e Det finns ett differentialområde. Följaktligen hittar jag torget själv genom att integrera dess differential. Inom den aktuella figuren varierar den oberoende variabeln L: från A till B, så det önskade området 5 kommer att vara 5 \u003d \\ f (x) dx. (I) Exempel 1. Beräkna området avgränsat av parabolen i - 1 s *, rakt x \u003d - FJ-, X \u003d 1 och axeln av * (bild 86). I fig. 87. Fig. 86. 1 här f (x) \u003d 1 - l?, Gränserna för integration a \u003d - och £ \u003d 1, därför j [* -t] \\ - -fl - m -1- ± l_ 1v1 -ll-II- ^ 3) | _ 2 3V 2 / J 3 24 24 * Exempel 2. Beräkna området avgränsat av sinusoid Y \u003d Sinxy Axis OH och rak (fig 87). Med hjälp av formel (I) får vi L 2 S \u003d J SinxDx \u003d [-COS X] Q \u003d 0 - (- 1) \u003d LF Exempel 3. Beräkna området, Begränsade bågeinusoider ^ y \u003d Sin JC, som ingåtts mellan två intilliggande Korsningspunkter med axeln OH (till exempel mellan koordinatens början och punkten med abscissen i). Observera att det framgår av de geometriska överväganden som detta område kommer att vara dubbelt så många områden i föregående exempel. Men vi gör beräkning: Jag är 5 \u003d | S \\ nxdx \u003d [- cosh) * - - cos I - (- cos 0) \u003d 1 + 1 \u003d 2. Åh, vårt antagande visade sig vara rättvist. Exempel 4. Beräkna området avgränsat av sinusoid och ^ axeln Oh på en ne rioode (fig 88). Preliminärt RAF-ris tyder på att området kommer att vara fyra gånger mer än i Ave. 2. Men gör beräkningar, vi får "Jag G, * I S - Sin X DX \u003d [- COS X] 0 \u003d \u003d - COS 2L - ( - Cos 0) \u003d - 1 + 1 \u003d 0. Detta resultat kräver förtydligande. För att bestämma kärnan i ärendet beräknar vi området avgränsat av samma sinusoid Y \u003d Sin L: och axeln OH, som sträcker sig från L till 2: e. Med hjälp av formel (I) får vi 2 liter $ 2L SIN XDX \u003d [- COSX] L \u003d -COS 2, ~) -C05Y \u003d - 1-1 \u003d -2. På så sätt ser vi att det här området visade sig vara negativt. Att jämföra det med ett område som beräknas i Ave. 3, vi får att deras absoluta värden är desamma, och tecknen är olika. Om du tillämpar v-egenskapen (se ch. Xi, § 4) fick jag 2 liter 2l J synd xdx \u003d j synd * dx [synd x dx \u003d 2 + (- 2) \u003d 0, vad som hände i det här exemplet är det inte Olycka. Alltid området under axeln OH, förutsatt att den oberoende variabeln ändras från vänster till höger, det visar sig när man beräknar med integralerna av negativa. I den här kursen kommer vi alltid att överväga kvadrater utan tecken. Därför är svaret i bara ett demonterat exempel att vara så: det önskade området är 2 + | -2 | \u003d 4. Exempel 5. Beräkna OAV-området som anges i fig. 89. Detta område är begränsat till axeln OH, parabola y \u003d - xg och rakt y - \u003d -x + \\. Området av det krökta trapeziet Det önskade området av OAV består av två delar: OAM och MAV. Sedan punkt A är en punkt av korsning av parabol och rakt, kommer dess koordinater att hitta lösa systemet med ekvationer 3 2 y \u003d tx. (Vi måste hitta bara abscissa poäng a). Lösa systemet hittar vi L; \u003d ~. Därför måste området beräknas i delar, första pl. Oam, och sedan pl. Mav: .... G 3 2, 3 g HP 3 1/2 i 2. Qam- ^ x och ändrar inte sitt tecken på det (Figur 1).Det kröklinjiga trapeziumområdet kan betecknas med S (g).

En specifik integrerad ʃ A B f (x) dx för funktionen f (x), som är kontinuerlig och icke-negativ på segmentet [a; b], och det finns ett område av motsvarande kröklinjiga trapezium.

Det vill säga att hitta området för figuren G, begränsad av linjerna Y \u003d F (x), Y \u003d 0, X \u003d A och X \u003d B, är det nödvändigt att beräkna en viss integrerad ʃ AB F (X ) DX.

På det här sättet, S (g) \u003d ʃ A b f (x) dx.

Om funktionen y \u003d f (x) inte är positiv på [a; b], då kan området för det kröklinjiga trapeziumet hittas med formeln S (g) \u003d -ʃ A b f (x) dx.

Exempel 1.

Beräkna området av figuren avgränsad av linjerna Y \u003d X3; y \u003d 1; x \u003d 2.

Beslut.

De angivna linjerna bildar en ABC-figur, som visas med kläckning på fikon. 2.

Det önskade området är lika med skillnaden mellan DACE Curvilinear Trapezium-områdena och Dabe-torget.

Med hjälp av formeln S \u003d ʃ A B F (x) dx \u003d s (b) - s (a) hittar vi integrationsgränserna. För att göra detta, lösa systemet med två ekvationer:

(y \u003d x 3,
(Y \u003d 1.

Således har vi X 1 \u003d 1 - den nedre gränsen och X \u003d 2 - den övre gränsen.

Så, s \u003d s dace - s dabe \u003d ʃ 1 2 x 3 dx - 1 \u003d x 4/4 | 1 2 - 1 \u003d (16 - 1) / 4 - 1 \u003d 11/4 (sq).

Svar: 11/4 kV. enheter.

Exempel 2.

Beräkna området av figuren begränsad av linjerna Y \u003d √h; y \u003d 2; x \u003d 9.

Beslut.

De angivna linjerna bildar en figur av ABC, som är begränsad från ovanför grafen

y \u003d √h, och under grafen av funktionen Y \u003d 2. Den resulterande figuren visas genom kläckning på fikon. 3.

Det önskade området är S \u003d ʃ A b (√x - 2). Vi hittar integrationsgränserna: B \u003d 9, för att hitta A, genom att lösa systemet med två ekvationer:

(y \u003d √h,
(y \u003d 2.

Således har vi det x \u003d 4 \u003d a är den nedre gränsen.

Så, s \u003d ∫ 4 9 (√x - 2) dx \u003d ∫ 4 9 √x dx-^ 4 9 2dx \u003d 2/3 x√ x | 4 9 - 2x | 4 9 \u003d (18 - 16/3) - (18 - 8) \u003d 2 2/3 (sq).

Svar: S \u003d 2 2/3 kvadratmeter. enheter.

Exempel 3.

Beräkna området i figuren, begränsad av linjerna Y \u003d x 3 - 4x; y \u003d 0; x ≥ 0.

Beslut.

Vi konstruerar ett diagram över funktionen Y \u003d x 3 - 4x på x ≥ 0. För att göra detta, hitta derivatet av ":

y '\u003d 3x 2 - 4, y' \u003d 0 vid x \u003d ± 2 / √3 ≈ 1.1 - kritiska punkter.

Om du avbildar kritiska punkter på den numeriska axeln och ställer in tecknen på derivatet, får vi att funktionen minskar från noll till 2 / √3 och ökar från 2 / √3 till plus oändlighet. Då är x \u003d 2 / √3 en minsta punkt, minimivärdet av funktionen i min \u003d -16 / (3√3) ≈ -3.

Vi definierar skärningspunkterna i grafen med koordinaternas axlar:

om x \u003d 0, sedan y \u003d 0, och därför, och (0; 0) - skärningspunkten med OU-axeln;

om y \u003d 0, sedan x 3 - 4x \u003d 0 eller x (x 2 - 4) \u003d 0, eller x (x - 2) (x + 2) \u003d 0, där x 1 \u003d 0, x 2 \u003d 2, x 3 \u003d -2 (ej lämplig, eftersom x ≥ 0).

Poäng A (0; 0) och i (2; 0) - grafens skärningspunkter med axeln OH.

De angivna linjerna bildar en figur av OAV, som visas med kläckning på fikon. fyra.

Eftersom funktionen y \u003d x 3 - 4x tar på (0; 2) ett negativt värde, då

S \u003d | ʃ 0 2 (x 3 - 4x) dx |.

Vi har: ʃ 0 2 (x 3 - 4x) dx \u003d (x 4/4 - 4x 2/2) | 0 2 \u003d -4, varifrån S \u003d 4 kvadratmeter. enheter.

Svar: S \u003d 4 kvadratmeter. enheter.

Exempel 4.

Hitta området av figuren begränsad av parabola y \u003d 2x 2 - 2x + 1, rak x \u003d 0, y \u003d 0 och tangent av denna parabole vid punkten med abscissa x 0 \u003d 2.

Beslut.

För det första är ekvationen tangent till parabole y \u003d 2x 2 - 2x + 1 vid punkten med abscissa xq \u003d 2.

Sedan derivatet Y '\u003d 4x - 2, sedan vid x 0 \u003d 2, erhåller vi k \u003d y' (2) \u003d 6.

Vi hittar ordinatpunkten för beröring: vid 0 \u003d 2 · 2 2 - 2 · 2 + 1 \u003d 5.

Följaktligen har ekvationen av tangent form: y - 5 \u003d 6 (x - 2) eller y \u003d 6x - 7.

Bygg en figurbegränsad linjer:

y \u003d 2x 2 - 2x + 1, y \u003d 0, x \u003d 0, y \u003d 6x - 7.

G y \u003d 2x 2 - 2x + 1 - parabola. Korsningspunkter med koordinataxlar: A (0; 1) - med OU-axeln; med axeln Oh - det finns inga skärningspunkter, för Ekvation 2x 2 - 2x + 1 \u003d 0 har inte lösningar (d< 0). Найдем вершину параболы:

x b \u003d 2/4 \u003d 1/2;

y B \u003d 1/2, det vill säga vertex parabolpunkt B har koordinater i (1/2; 1/2).

Så, den siffra vars område är skyldig att bestämma visas av kläckning på fikon. fem.

Vi har: s o a i d \u003d s oabc - s adbc.

Vi hittar koordinaterna för punkten d från villkoret:

6x - 7 \u003d 0, dvs. X \u003d 7/6 betyder det DC \u003d 2 - 7/6 \u003d 5/6.

DBC-triangelområde Sök enligt formeln S ADBC \u200b\u200b\u003d 1/2 · DC · BC. På det här sättet,

S adbc \u003d 1/2 · 5/6 · 5 \u003d 25/12 kV. enheter.

S oabc \u003d ʃ 0 2 (2x 2 - 2x + 1) dx \u003d (2x 3/3 - 2x 2/2 + x) | 0 2 \u003d 10/3 (sq. Mat.).

Vi får äntligen: S o a i d \u003d s oabc - s adbc \u003d 10/3 - 25/12 \u003d 5/4 \u003d 1 1/4 (sq. M. uzh).

Svar: S \u003d 1 1/4 kV. enheter.

Vi demonterade exempel hitta kvadraterna av figurer som är begränsade av de angivna linjerna. För att framgångsrikt lösa sådana uppgifter måste du kunna bygga på planen för linjen och graferna av funktioner, hitta punkterna för korsning av linjer, applicera formeln för att hitta området, vilket innebär närvaro av färdigheter och färdigheter för beräkning av vissa integraler.

webbplatsen, med full eller partiell kopiering av materialreferensen till den ursprungliga källan krävs.

Alla speciella integrerade (som existerar) har en mycket god geometrisk mening. I lektionen sa jag att ett visst integral är ett nummer. Och nu är det dags att ange ett annat användbart faktum. Ur geometri synvinkel är ett visst integral ett område.

Dvs, ett specifikt integrerat (om det existerar) geometriskt motsvarar området för någon figur. Tänk till exempel ett specifikt integrerat. Integrand-funktionen ställer in en kurva på planet (det kan alltid dras om så önskas), och en viss integral i sig är numeriskt lika med området av motsvarande kröktrapinär trapezium.

Exempel 1.

Detta är en typisk uppgiftsformulering. Den första och viktigaste punkten i beslutet - Att bygga en ritning. Och ritningen måste byggas RÄTT.

När du bygger en ritning rekommenderar jag följande ordning: först Det är bättre att bygga allt rakt (om de är) och bara senare - Paraboler, hyperbolor, scheman av andra funktioner. Funktionsgrafer är mer lönsamma att bygga potkoTekniken för incheckningskonstruktion finns i referensmaterialet.

Där kan du också hitta ett mycket användbart material i förhållande till vår lektion. Materialet - hur man snabbt bygger en parabola.

I den här uppgiften kan beslutet se ut så.
Utför ritningen (Observera att ekvationen ställer in axeln):

Jag kommer inte att stroke en kröktrapeze, det är uppenbart här om vilket område det finns ett tal. Beslutet fortsätter så här:

På segmentet Schema är en funktion belägen Över axeln, så:

Svar:

Vem har svårigheter med beräkningen av en viss integrerad och användningen av Newton-Leibnia-formel , hänvisa till föreläsningen Vissa integrerade. Exempel på lösningar.

Efter att uppgiften är klar är det alltid användbart att titta på ritningen och uppskatta, den verkliga som visade sig. I det här fallet, "på ögonen", räknar vi antalet celler på ritningen - ja, ungefär 9 kommer att flöda, det verkar som om sanningen. Det är helt klart att om vi hade sagt svar: 20 kvadratiska enheter är det uppenbart att ett fel görs någonstans - i den 20 cellerna är det klart inte monterat, från styrkan hos ett dussin. Om svaret visade sig, bestäms också uppgiften felaktigt.

Exempel 2.

Beräkna området för form, begränsade linjer och axel

Detta är ett exempel på en oberoende lösning. Komplett lösning och svar i slutet av lektionen.

Vad ska man göra om det krökta trapeziet är beläget under axeln?

Exempel 3.

Beräkna området för formen, begränsade linjer och koordinataxlarna.

Lösning: Utför ritning:

Om ett curvilinear trapezium fullt beläget under axeln, då kan dess område hittas med formeln:
I detta fall:

Uppmärksamhet! Förvirra inte två typer av uppgifter:

1) Om du är inbjuden att lösa ett enkelt integrerat utan geometrisk mening, kan det vara negativt.

2) Om du är inbjuden att hitta figuren i figuren med hjälp av ett specifikt integrerat, är området alltid positivt! Det är därför i bara den ansedda formeln visas minus.

I praktiken är siffran oftast i övre och nedre halvplanet, och därför, från de enklaste skoldiagrammen, gå till mer meningsfulla exempel.

Exempel 4.

Hitta området för en platt figur, begränsade linjer ,.

Lösning: Först måste du rita en ritning. Generellt sett, när vi bygger en ritning i uppgifter till området, är vi mest intresserade av korsningspunkterna i linjerna. Hitta poäng för korsning av parabola och direkt. Detta kan göras på två sätt. Den första metoden är analytisk. Vi löser ekvationen:

Så, den lägre integrationsgränsen, den övre gränsen för integration.
Det här är bättre, om möjligt, använd inte.

Det är mycket mer lönsamt och snabbare att bygga linjerna i linjen, medan integrationsgränserna klargörs som om "av sig själva". Tekniken för upphörandet för olika grafer anses i detalj i hjälpen Diagram och egenskaper hos elementära funktioner. Ett analytiskt sätt att hitta gränserna trots allt är det ibland nödvändigt att tillämpa om schemat är tillräckligt stort, eller en utbildad konstruktion avslöjade inte integrationsgränserna (de kan vara fraktionella eller irrationella). Och ett sådant exempel, vi överväger också.

Vi återvänder till vår uppgift: mer rationell först bygga en rak linje och bara då parabola. Utför ritning:

Jag upprepar att i den nuvarande konstruktionen, är integrationsgränserna oftast ut av den "automatiska".

Och nu arbetsformeln: Om på segmentet någon kontinuerlig funktion mer eller lika En del kontinuerlig funktion, området för motsvarande figur kan hittas med formeln:

Här är det inte längre nödvändigt att tänka där figuren är belägen - över axeln eller under axeln, och, ungefär, viktigt vad är grafen ovan(i förhållande till ett annat schema) och vad - nedan.

I det här exemplet är det uppenbart att på segmentet av parabol ligger ovanför rakt, och därför är det nödvändigt att subtrahera

Slutförandet av lösningen kan se ut så här:

Den önskade siffran är begränsad till parabolen ovanifrån och direkt botten.
På segmentet, enligt motsvarande formel:

Svar:

Faktum är att skolformeln för det kröklinjiga trapezium i det nedre halvplanet (se enkelt exempel nr 3) - ett speciellt fall med formel . Eftersom axeln definieras av ekvationen, och funktionsgrafen är belägen under axeln,

Och nu ett par exempel för ett självständigt beslut

Exempel 5.

Exempel 6.

Hitta området för de begränsade linjerna ,.

Under löpande uppgifter för att beräkna området med ett specifikt integrerat, uppstår ett roligt fall ibland. Ritningen är klar korrekt, beräkningar - rätt, men intensifierad ... hittade området är inte figurenAtt det här är hur din ödmjuka tjänare packades. Här är ett riktigt fall från livet:

Exempel 7.

Beräkna området för formen, begränsade linjer ,,,.

Förstekta ritningen:

Figur vars område vi behöver hitta är skuggade i blått(Se noggrant ut på villkoret - än figuren är begränsad!). Men i praktiken på ouppmärksamhet är det ofta att det är nödvändigt att hitta området i figuren, som är skuggat med grönt!

Detta exempel är också användbart genom att det anses vara i det storleken på två specifika integraler. Verkligen:

1) Ett rakt schema är beläget på segmentet över axeln;

2) På segmentet över axeln finns ett graf av hyperboler.

Det är uppenbart att torget kan (och behöver) att sönderdelas, så:

Svar:

Exempel 8.

Beräkna området för formen, begränsade linjer,
Föreställ dig ekvationen i "skolans" -formulär och utföra den aktuella ritningen:

Från ritningen är det tydligt att den övre gränsen vi har "bra" :.
Men vad är den nedre gränsen?! Det är uppenbart att detta inte är ett heltal, men vad? Kanske ? Men var är garantin att ritningen är gjord med perfekt noggrannhet, det kan väl vara det. Eller rot. Och om vi i allmänhet har ett felaktigt byggt ett schema?

I sådana fall måste du spendera extra tid och ange integrationsgränserna analytiskt.

Hitta skärningspunkterna i direkt och parabola.
För att göra detta, lösa ekvationen:

Därav, .

Ytterligare lösning är trivial, det viktigaste är att inte bli förvirrad i substitutioner och tecken, beräkningarna här är inte det enklaste.

På att skära Enligt motsvarande formel:

Svar:

Tja, och i slutsatsen av lektionen, överväga två uppgifter svårare.

Exempel 9.

Beräkna formen av formen, begränsade linjer ,,

Lösning: Visa denna form i ritningen.

För den nuvarande konstruktionen av ritningen är det nödvändigt att känna till sinusoidernas utseende (och det är allmänt användbart att veta grafer av alla elementära funktioner), liksom vissa sinusvärden, kan de hittas i trigonometriskt bord. I vissa fall (som i detta) får det bygga en schematisk ritning som graferna och integrationsgränserna måste återspeglas i princip.

Med gränserna för integration finns det inga problem här, de följer direkt från villkoret: - "X" varierar från noll till "PI". Vi utarbetar en ytterligare lösning:

På segmentet är funktionsdiagrammet ovan ovanför axeln, så:

(1) Hur man integrerar bihålor och cosines i udda grader kan ses i lektionen Integreringar från trigonometriska funktioner. Detta är en typisk mottagning, pressning av en sinus.

(2) Vi använder den viktigaste trigonometriska identiteten i form av

(3) Vi kommer att ersätta variabeln, då:

Ny ändringsintegration:

Vem har mycket dåliga saker med ersättningar, vänligen gå till lektionen Ersättningsmetod i en obestämd integral. Vem är inte särskilt tydlig för ersättningsalgoritmen i ett visst integrerat, besök sidan Vissa integrerade. Exempel på lösningar.

Introduktion

Att hitta ett derivat F "(x) eller differential df \u003d f" (x) dx funktion f (x) är den huvudsakliga uppgiften för differentialalkylus. I den integrerade beräkningen är det inverse problemet löst: enligt en given funktion F (x) krävs det att hitta en sådan funktion f (x), vilken f "(x) \u003d f (x) eller f (x) \u003d f "(x) dx \u003d f (x) dx. Således är den huvudsakliga uppgiften att integrera kalkylen återställandet av funktionen F (x) enligt den kända derivaten (differential) av denna funktion. Integrerande beräkning har många tillämpningar inom geometri, mekanik, fysik och teknik. Det ger en allmän metod för att hitta utrymme, volymer, tyngdkraftscentra etc.

Körningen av matematisk analys innehåller en mängd olika material, men en av dess centrala partitioner är ett specifikt integrerat. Integreringen av många typer av funktioner är ibland en av de svåraste problemen med matematisk analys.

Beräkning av ett specifikt integrerat har inte bara teoretiskt intresse. Det är ibland reducerat till dess beräkning, de uppgifter som är förknippade med en persons praktiska aktiviteter reduceras.

Även begreppet en specifik integral används i stor utsträckning i fysik.

Hitta området för det kröklinjiga trapezium

Ett curvilinear trapezium kallas en figur belägen i ett rektangulärt koordinatsystem och en begränsad abscissaxel, direkt x \u003d A. och x \u003d B. och kurvan och icke-negativa på segmentet. Cirka området för det kröklinjiga trapeziumet kan hittas så här:

1. För att dela upp avskuren av abscissaxeln på n. lika stora segment;

2. Gör sektionerna av segmenten vinkelrätt mot abscissaxeln, till korsningen med kurvan;

3. Byt ut de resulterande rektangelkolumnerna med en bas och en höjd som är lika med värdet av funktionen f. i vänstra änden av varje segment;

4. Hitta summan av kvadraterna i dessa rektanglar.

Men du kan hitta området för curvilinear annars: enligt formeln Newton Labitsa. För att bevisa den formel som börjar, visar vi att området för det kröklinjiga trapezium är lika med, var - någon av de primitiva funktionerna vars graf begränsar det kröklinjiga trapeziumet.

Beräkningen av området för det krökta trapeziumet är skrivet enligt följande:

1. Det finns några av de primitiva funktionerna.

2. Inspelad. - Detta är en Newton-Leibniz-formel.

Hitta området för den krökta sektorn

Tänk på kurvan? \u003d? (?) I polarkoordinatsystemet, var? (?) - Kontinuerlig och icke-negativ på [? ?] Funktion. Figur, begränsad kurva? (?) och strålar? \u003d?,? \u003d?, kallas den kröklösa sektorn. Området av den krökmässiga sektorn är lika med

Hitta längden på bågskurvan

Rektangulära koordinater

Antag i rektangulära koordinater ges en platt kurva AB, vars ekvation y \u003d f (x), där a? x? b. (Figur 2)

Under båglängden förstås AB som den gräns som längden på den trasiga linjen, inskriven i den här bågen, när antalet knullar av den brutna blir alltmer, och längden på den största länken ska sträva efter noll.

Ansök schema I (summering).

Poäng x \u003d a, x, ..., x \u003d b (x? X? X \u003d b (x? X? X) Svår segmentet på n delar. Låt dessa punkter motsvara punkterna M \u003d A, M, ..., M \u003d B på AB-kurvan. Vi kommer att göra ackord mm, mm, ..., mm, vars längder betecknas med respektive till? L, ...,? L.

Vi får trasig mmm ... mm, vars längd är l \u003d? L +? L + ... +? L \u003d? L.

Längden på ackordet (eller Lymannaya Link)? Jag finns på Pythagoree-teoremet från en triangel med tull? X och? Y:

L \u003d, var? X \u003d x - x,? Y \u003d f (x) - f (x).

Enligt Lagrange-teoremet på den slutliga ökningen av funktionen

Y \u003d (c)? X, där c (x, x).

och längden på all trasig mmm ... mm är lika

Längden på AB-kurvan, per definition, är lika

Observera att när? L 0 också och? X 0 (? L \u003d och därför |? X |< ?L). Функция непрерывна на отрезке , так как, по условию, непрерывна функция f (X). Следовательно, существует предел интегральной суммы L=?L= , кода max ?X 0:

Således L \u003d DX.

Exempel: Hitta längden på radius R. (fig 3)

Hitta? Del av dess längd från punkten (0; r) till punkten (r; 0). Som

№ ____ Datum ________

Ämne:Curvilinear trapezium och dess kvadrat b

Mål lektion: Ge definitionen av ett kröktrapinärt trapezium och dess kvadrat, lär sig att beräkna området för det kröklinjiga trapeziumet.

Under klasserna

1. Organisationsmoment.

Hälsningsstudenter, kontroll av klassens beredskap för lektion, organisation av studentens uppmärksamhet, avslöjande av de allmänna målen för lektionen och dess plan.

2. Stage kontrollerar läxor.

Mål: fastställa rättighet, fullständighet och medvetenhet om genomförandet av D / S alla studenter, identifiera luckor i kunskap och sätt att elevernas verksamhet. Bestäm orsakerna till förekomsten av svårigheter, eliminera de upptäckta utrymmena.

3. Topp uppdatering.

Uppgifter: Ge motivation av skolbarns läror, inkludering i gemensamma aktiviteter för att bestämma målen för lektionen. Aktualisera subjektiva studentupplevelse.

Minns de grundläggande begreppen och formlerna.

Definition. Fungera y \u003d.f.(x), x (A, b), Kallas primitiv för funktion y \u003d f (x), x (A, b), Om för alla x. (A, b) Jämställdhet utförs

F. (x) \u003d f (x).

Kommentar. Om en f.(x) Det finns en primitiv för funktion f (x), sedan med någon konstant FRÅN, F (x) + c är också en primitiv för f (x).

Uppgiften att hitta alla primitiva funktioner f (x) kallad integration, och uppsättningen av all primär kallas en osäker integrerad för funktionen f (x) förbi DX. Och betecknar

Egenskaper inkluderar:

1. ;

2. Om en C \u003d.Const, T.
;

3.
.

Kommentar. I skolans kurs, används inte termen "obestämd integrerad", istället säger de "många av alla primordiala".

Vi ger ett bord av osäkra integraler.

Exempel 1. Hitta en primär för funktion
passerar genom punkten M.(2;4).

Beslut. Många av alla primitiva funktioner
Det finns en obestämd integral
. Jag beräknar den med hjälp av egenskaperna hos det integrerade 1 och 2. Vi har:

Mottog att uppsättningen av alla primitiva ges av familjen av funktioner y \u003d f (x) + c, dvs y \u003d x. 3 – 2x + C.var FRÅN - godtycklig konstant.

Vet att primäret passerar genom punkten M.(2; 4), kommer vi att ersätta sina koordinater i föregående uttryck och hitta FRÅN.

4=2 3 –2 2+FRÅN  FRÅN=4–8+4; FRÅN=0.

Svar: F (x) \u003d x 3 - 2x. - den önskade primitiva.

4. Bildning av nya koncept och metoder för åtgärder.

Uppgifter: Se till att uppfattningen, förståelse och memoriserande student under det material som studeras. Se till att inlärningsmetoden för reproduktion av det studerade materialet, främja den filosofiska förståelsen av lämpliga begrepp, lagar, regler, formler. För att fastställa korrektheten och medvetenheten om det studerade materialet som lärt sig, att identifiera luckorna i primär förståelse, genomföra korrigering. Ge korrelerat av studenter av sin subjektiva erfarenhet av tecken på vetenskaplig kunskap.

Hitta ansikten av platta figurer

Uppgiften att hitta ett område med en platt figur är nära relaterat till uppgiften att hitta primitiv (integration). Nämligen: området för det krökta trapeziumbegränsade grafeny \u003d f (x) (f (x)\u003e 0) Straightx \u003d a; x \u003d b; y \u003d. 0, lika med skillnadsskillnadsvärdena för funktioneny \u003d f (x) På punkterb. ocha. :

S \u003d f (b) -f (a)

Låt oss ge definitionen av ett specifikt integrerat.

HANDLA OM
förhållande. Låt funktionen y \u003d f (x) Definierad och integrerbar på segmentet [ a, B.] släpp det F (x) - några av hennes primitiva. Då numret F (b) -f (a) kallad integral ot. men innan b. Funktioner f (x) Och betecknar

.

Jämlikhet
kallad Newton Labitsa formel.

Denna formel förbinder uppgiften att hitta en platt figur med ett integrerat.

I allmänhet, om siffran är begränsad till grafer av funktioner y \u003d f (x); Y \u003d g (x) (f (x)\u003e g (x)) Och rakt x \u003d A.; X \u003d B.då är dess område lika:

.

Exempel2. Vid vilken tidpunkt är funktionsschemat y \u003d x. 2 + 1 Det är nödvändigt att hålla en tangent, så att den skär ut från figuren som bildas av schemat för denna funktion och rakt y \u003d.0, x \u003d0, x \u003d1 trapezing den största torget?

Beslut. Låt vara M. 0 (X. 0 , y. 0 ) - Funktionsgrafikfunktion y \u003d x. 2 + 1, där den önskade tangenten.

Hitta ekvationen tangent y \u003d y. 0 + F. (X. 0 ) (X-x 0 ) .

Vi har:

därför

.

Hitta trapesens torg Oayks.

.

B. - Korsning av tangent med direkt x \u003d.1 

Uppgiften reduceras för att hitta det största värdet av funktionen.

S.(x.)\u003d -X. 2 + X +.1 på segmentet. Hitta S. (x.)=– 2x +.1. Hitta en kritisk punkt från villkoret S. (x.)= 0  x \u003d..

Vi ser att funktionen når det största värdet när x \u003d.. Hitta
.

Svar: Tangentiskt måste spendera på punkt
.

Observera att uppgiften att hitta integralen ofta, baserat på dess geometriska mening. Låt oss visa på exemplet hur en sådan uppgift är löst.

Exempel 4. Med hjälp av den integrerade geometriska betydelsen för att beräkna

men )
; b)
.

Beslut.

men)
- lika med området för det krökta trapezium, begränsade linjer.

F reformera

- Övre halvan av cirkeln med mitten R(1; 0) och radie R \u003d.1.

därför
.

Svar: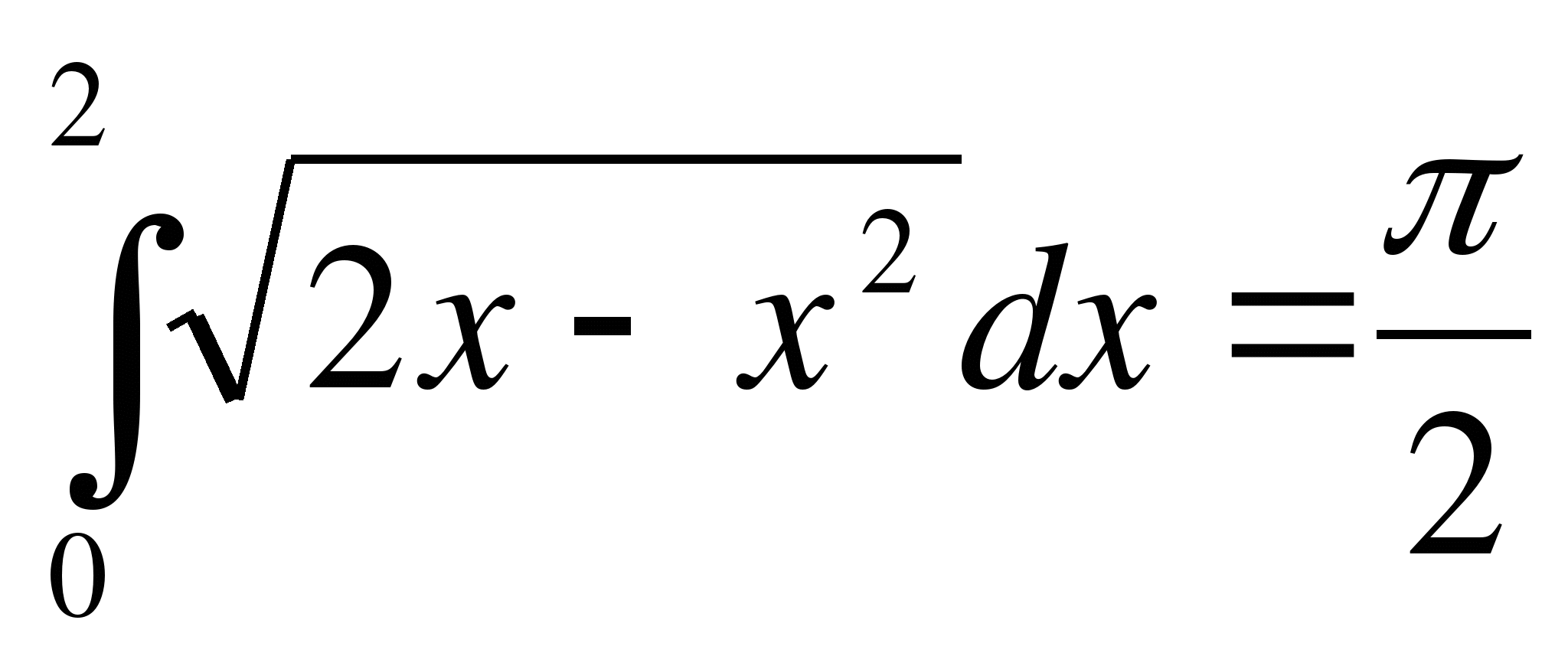
.

b) Att argumentera på samma sätt, kommer vi att bygga en region begränsad av diagram .2 – 2x +.2, tangent till det på poäng A.
, B.(4;2)

y \u003d.–9x-59, parabola y \u003d.3x. 2 + AX +.1, om du vet att tangent till parabolen vid punkten x \u003d -2 är med axeln OXE. Storleksvinkeln arctg.6.

Att hitta menOm det är känt att området för det krökta trapeziumet begränsas y \u003d.3x. 3 + 2x, X \u003d A, Y \u003d0, lika med en.

Hitta det minsta värdet av området av figuren begränsad av parabola y \u003d x. 2 + 2x-3 och direkt y \u003d kx +1.

6.Tap information om dina läxor.

Uppgifter: För att säkerställa en förståelse för målen, innehållet och metoderna för läxor.308, 19,20,21 udda

7.Instation av lektionen.

Uppgift: Ge en kvalitativ bedömning av klassarbete och enskilda studenter.