How to simplify an expression 8. Converting expressions. Detailed theory (2019). Additional simplification methods
At the beginning of the lesson, we will review the basic properties of square roots, and then look at several complex examples of simplifying expressions containing square roots.
Subject:Function. Properties of square root
Lesson:Converting and simplifying more complex expressions with roots
1. Review of the properties of square roots
Let us briefly repeat the theory and recall the basic properties of square roots.
Properties of square roots:
1. therefore, ;
3. ![]() ;
;
4. ![]() .
.
2. Examples for simplifying expressions with roots
Let's move on to examples of using these properties.
Example 1: Simplify an expression ![]() .
.
Solution. To simplify, the number 120 must be factorized into prime factors:
We will reveal the square of the sum using the appropriate formula:
Example 2: Simplify an expression ![]() .
.
Solution. Let us take into account that this expression does not make sense for all possible values of the variable, since this expression contains square roots and fractions, which leads to a “narrowing” of the range of permissible values. ODZ:  ().
().
Let's bring the expression in brackets to the common denominator and write the numerator of the last fraction as the difference of squares:
Answer. at.
Example 3: Simplify an expression ![]() .
.
Solution. It can be seen that the second numerator bracket has an inconvenient appearance and needs to be simplified; let’s try to factor it using the grouping method.
To be able to derive a common factor, we simplified the roots by factoring them. Let's substitute the resulting expression into the original fraction:
After reducing the fraction, we apply the difference of squares formula.
3. An example of getting rid of irrationality
Example 4. Free yourself from irrationality (roots) in the denominator: a) ; b) .
Solution. a) In order to get rid of irrationality in the denominator, the standard method of multiplying both the numerator and denominator of a fraction by the conjugate factor to the denominator is used (the same expression, but with the opposite sign). This is done to complement the denominator of the fraction to the difference of squares, which allows you to get rid of the roots in the denominator. Let's do this in our case:
b) perform similar actions:
4. Example for proof and identification of a complete square in a complex radical
Example 5. Prove equality ![]() .
.
Proof. Let's use the definition of a square root, from which it follows that the square of the right-hand expression must be equal to the radical expression:
![]() . Let's open the brackets using the formula for the square of the sum:
. Let's open the brackets using the formula for the square of the sum:
![]() , we got the correct equality.
, we got the correct equality.
Proven.
Example 6. Simplify the expression.
Solution. This expression is usually called a complex radical (root under root). In this example, you need to figure out how to isolate a complete square from the radical expression. To do this, note that of the two terms, it is a candidate for the role of the double product in the formula for the squared difference (difference, since there is a minus). Let us write it in the form of the following product: , then 1 claims to be one of the terms of a complete square, and 1 claims to be the second.
Let's substitute this expression under the root.
Simplifying algebraic expressions is one of the keys to learning algebra and is an extremely useful skill for all mathematicians. Simplification allows you to reduce a complex or long expression to a simple expression that is easy to work with. Basic skills of simplification are good even for those who are not enthusiastic about mathematics. By following a few simple rules, you can simplify many of the most common types of algebraic expressions without any special mathematical knowledge.
Steps
Important Definitions
-
Similar members . These are members with a variable of the same order, members with the same variables, or free members (members that do not contain a variable). In other words, similar terms include the same variable to the same degree, include several of the same variables, or do not include a variable at all. The order of the terms in the expression does not matter.
- For example, 3x 2 and 4x 2 are similar terms because they contain a second-order (to the second power) variable "x". However, x and x2 are not similar terms, since they contain the variable “x” of different orders (first and second). Likewise, -3yx and 5xz are not similar terms because they contain different variables.
-
Factorization . This is finding numbers whose product leads to the original number. Any original number can have several factors. For example, the number 12 can be factored into the following series of factors: 1 × 12, 2 × 6 and 3 × 4, so we can say that the numbers 1, 2, 3, 4, 6 and 12 are factors of the number 12. The factors are the same as the factors , that is, the numbers by which the original number is divided.
- For example, if you want to factor the number 20, write it like this: 4×5.
- Note that when factoring, the variable is taken into account. For example, 20x = 4(5x).
- Prime numbers cannot be factored because they are only divisible by themselves and 1.
-
Remember and follow the order of operations to avoid mistakes.
- Brackets
- Degree
- Multiplication
- Division
- Addition
- Subtraction
Bringing similar members
-
Write down the expression. Simple algebraic expressions (those that don't contain fractions, roots, etc.) can be solved (simplified) in just a few steps.
- For example, simplify the expression 1 + 2x - 3 + 4x.
-
Define similar terms (terms with a variable of the same order, terms with the same variables, or free terms).
- Find similar terms in this expression. The terms 2x and 4x contain a variable of the same order (first). Also, 1 and -3 are free terms (do not contain a variable). Thus, in this expression the terms 2x and 4x are similar, and the members 1 and -3 are also similar.
-
Give similar terms. This means adding or subtracting them and simplifying the expression.
- 2x + 4x = 6x
- 1 - 3 = -2
-
Rewrite the expression taking into account the given terms. You will get a simple expression with fewer terms. The new expression is equal to the original one.
- In our example: 1 + 2x - 3 + 4x = 6x - 2, that is, the original expression is simplified and easier to work with.
-
Follow the order of operations when bringing similar members. In our example, it was easy to provide similar terms. However, in the case of complex expressions in which terms are enclosed in parentheses and fractions and roots are present, it is not so easy to bring such terms. In these cases, follow the order of operations.
- For example, consider the expression 5(3x - 1) + x((2x)/(2)) + 8 - 3x. Here it would be a mistake to immediately define 3x and 2x as similar terms and present them, because it is necessary to open the parentheses first. Therefore, perform the operations according to their order.
- 5(3x-1) + x((2x)/(2)) + 8 - 3x
- 15x - 5 + x(x) + 8 - 3x
- 15x - 5 + x 2 + 8 - 3x. Now, when the expression contains only addition and subtraction operations, you can bring similar terms.
- x 2 + (15x - 3x) + (8 - 5)
- x 2 + 12x + 3
- For example, consider the expression 5(3x - 1) + x((2x)/(2)) + 8 - 3x. Here it would be a mistake to immediately define 3x and 2x as similar terms and present them, because it is necessary to open the parentheses first. Therefore, perform the operations according to their order.
Taking the multiplier out of brackets
-
Find greatest common divisor(GCD) of all coefficients of the expression. GCD is the largest number by which all coefficients of the expression are divided.
- For example, consider the equation 9x 2 + 27x - 3. In this case, GCD = 3, since any coefficient of this expression is divisible by 3.
-
Divide each term of the expression by gcd. The resulting terms will contain smaller coefficients than in the original expression.
- In our example, divide each term in the expression by 3.
- 9x 2 /3 = 3x 2
- 27x/3 = 9x
- -3/3 = -1
- The result was an expression 3x 2 + 9x - 1. It is not equal to the original expression.
- In our example, divide each term in the expression by 3.
-
Write down the original expression as equal to the product of gcd and the resulting expression. That is, enclose the resulting expression in brackets, and take the gcd out of the brackets.
- In our example: 9x 2 + 27x - 3 = 3(3x 2 + 9x - 1)
-
Simplifying fractional expressions by putting the factor out of brackets. Why simply put the multiplier out of brackets, as was done earlier? Then, to learn how to simplify complex expressions, such as fractional expressions. In this case, putting the factor out of brackets can help get rid of the fraction (from the denominator).
- For example, consider the fractional expression (9x 2 + 27x - 3)/3. Use factoring out to simplify this expression.
- Put the factor of 3 out of brackets (as you did earlier): (3(3x 2 + 9x - 1))/3
- Notice that there is now a 3 in both the numerator and the denominator. This can be reduced to give the expression: (3x 2 + 9x – 1)/1
- Since any fraction that has the number 1 in the denominator is simply equal to the numerator, the original fractional expression simplifies to: 3x 2 + 9x - 1.
- For example, consider the fractional expression (9x 2 + 27x - 3)/3. Use factoring out to simplify this expression.
Additional simplification methods
-
Simplifying fractional expressions. As noted above, if both the numerator and denominator contain the same terms (or even the same expressions), then they can be reduced. To do this, you need to take out of brackets the common factor of the numerator or the denominator, or both the numerator and the denominator. Or you can divide each term in the numerator by the denominator and thus simplify the expression.
- For example, consider the fractional expression (5x 2 + 10x + 20)/10. Here, simply divide each numerator term by the denominator (10). But note that the term 5x 2 is not evenly divisible by 10 (since 5 is less than 10).
- So write a simplified expression like this: ((5x 2)/10) + x + 2 = (1/2)x 2 + x + 2.
- For example, consider the fractional expression (5x 2 + 10x + 20)/10. Here, simply divide each numerator term by the denominator (10). But note that the term 5x 2 is not evenly divisible by 10 (since 5 is less than 10).
-
Simplification of radical expressions. Expressions under the root sign are called radical expressions. They can be simplified through their decomposition into appropriate factors and the subsequent removal of one factor from under the root.
- Let's look at a simple example: √(90). The number 90 can be factored into the following factors: 9 and 10, and from 9 we can take the square root (3) and take 3 out from under the root.
- √(90)
- √(9×10)
- √(9)×√(10)
- 3×√(10)
- 3√(10)
- Let's look at a simple example: √(90). The number 90 can be factored into the following factors: 9 and 10, and from 9 we can take the square root (3) and take 3 out from under the root.
-
Simplifying expressions with powers. Some expressions contain operations of multiplication or division of terms with powers. In the case of multiplying terms with the same base, their powers are added; in the case of dividing terms with the same base, their degrees are subtracted.
- For example, consider the expression 6x 3 × 8x 4 + (x 17 /x 15). In the case of multiplication, add the powers, and in the case of division, subtract them.
- 6x 3 × 8x 4 + (x 17 /x 15)
- (6 × 8)x 3 + 4 + (x 17 - 15)
- 48x 7 + x 2
- The following is an explanation of the rules for multiplying and dividing exponent terms.
- Multiplying terms with powers is equivalent to multiplying terms by themselves. For example, since x 3 = x × x × x and x 5 = x × x × x × x × x, then x 3 × x 5 = (x × x × x) × (x × x × x × x × x), or x 8 .
- Likewise, dividing terms with degrees is equivalent to dividing terms by themselves. x 5 /x 3 = (x × x × x × x × x)/(x × x × x). Since similar terms found in both the numerator and the denominator can be reduced, the product of two “x”, or x 2 , remains in the numerator.
- For example, consider the expression 6x 3 × 8x 4 + (x 17 /x 15). In the case of multiplication, add the powers, and in the case of division, subtract them.
Rational expressions and fractions are the cornerstone of the entire algebra course. Those who learn to work with such expressions, simplify them and factor them, will essentially be able to solve any problem, since transforming expressions is an integral part of any serious equation, inequality, or even word problem.
In this video tutorial we will look at how to correctly use abbreviated multiplication formulas to simplify rational expressions and fractions. Let's learn to see these formulas where, at first glance, there is nothing. At the same time, we will repeat such a simple technique as factoring a quadratic trinomial through a discriminant.
As you probably already guessed from the formulas behind me, today we will study abbreviated multiplication formulas, or, more precisely, not the formulas themselves, but their use to simplify and reduce complex rational expressions. But, before moving on to solving examples, let's take a closer look at these formulas or remember them:
- $((a)^(2))-((b)^(2))=\left(a-b \right)\left(a+b \right)$ — difference of squares;
- $((\left(a+b \right))^(2))=((a)^(2))+2ab+((b)^(2))$ is the square of the sum;
- $((\left(a-b \right))^(2))=((a)^(2))-2ab+((b)^(2))$ — squared difference;
- $((a)^(3))+((b)^(3))=\left(a+b \right)\left(((a)^(2))-ab+((b)^( 2)) \right)$ is the sum of cubes;
- $((a)^(3))-((b)^(3))=\left(a-b \right)\left(((a)^(2))+ab+((b)^(2) ) \right)$ is the difference of cubes.
I would also like to note that our school education system is structured in such a way that it is with the study of this topic, i.e. rational expressions, as well as roots, modules, all students have the same problem, which I will now explain.
The fact is that at the very beginning of studying abbreviated multiplication formulas and, accordingly, actions to reduce fractions (this is somewhere in the 8th grade), teachers say something like the following: “If something is not clear to you, then don’t worry, we will help you.” We will return to this topic more than once, in high school for sure. We'll look into this later." Well, then, at the turn of 9-10 grades, the same teachers explain to the same students who still don’t know how to solve rational fractions, something like this: “Where were you the previous two years? This was studied in algebra in 8th grade! What could be unclear here? It’s so obvious!”
However, such explanations do not make it any easier for ordinary students: they still had a mess in their heads, so right now we will look at two simple examples, on the basis of which we will see how to isolate these expressions in real problems, which will lead us to abbreviated multiplication formulas and how to then apply this to transform complex rational expressions.
Reducing simple rational fractions
Task No. 1
\[\frac(4x+3((y)^(2)))(9((y)^(4))-16((x)^(2)))\]
The first thing we need to learn is to identify exact squares and higher powers in the original expressions, on the basis of which we can then apply formulas. Let's get a look:
Let's rewrite our expression taking into account these facts:
\[\frac(4x+3((y)^(2)))(((\left(3((y)^(2)) \right))^(2))-((\left(4x \right))^(2)))=\frac(4x+3((y)^(2)))(\left(3((y)^(2))-4x \right)\left(3 ((y)^(2))+4x \right))=\frac(1)(3((y)^(2))-4x)\]
Answer: $\frac(1)(3((y)^(2))-4x)$.
Problem No. 2
Let's move on to the second task:
\[\frac(8)(((x)^(2))+5xy-6((y)^(2)))\]
There is nothing to simplify here, because the numerator contains a constant, but I proposed this problem precisely so that you learn how to factor polynomials containing two variables. If instead we had the polynomial below, how would we expand it?
\[((x)^(2))+5x-6=\left(x-... \right)\left(x-... \right)\]
Let's solve the equation and find the $x$ that we can put in place of the dots:
\[((x)^(2))+5x-6=0\]
\[((x)_(1))=\frac(-5+7)(2)=\frac(2)(2)=1\]
\[((x)_(2))=\frac(-5-7)(2)=\frac(-12)(2)=-6\]
We can rewrite the trinomial as follows:
\[((x)^(2))+5xy-6((y)^(2))=\left(x-1 \right)\left(x+6 \right)\]
We learned how to work with a quadratic trinomial - that's why we needed to record this video lesson. But what if, in addition to $x$ and a constant, there is also $y$? Let's consider them as another element of the coefficients, i.e. Let's rewrite our expression as follows:
\[((x)^(2))+5y\cdot x-6((y)^(2))\]
\[((x)_(1))=\frac(-5y+7y)(2)=y\]
\[((x)_(2))=\frac(-5y-7y)(2)=\frac(-12y)(2)=-6y\]
Let us write the expansion of our square construction:
\[\left(x-y \right)\left(x+6y \right)\]
So, if we return to the original expression and rewrite it taking into account the changes, we get the following:
\[\frac(8)(\left(x-y \right)\left(x+6y \right))\]
What does such a record give us? Nothing, because it cannot be reduced, it is not multiplied or divided by anything. However, as soon as this fraction turns out to be an integral part of a more complex expression, such an expansion will come in handy. Therefore, as soon as you see a quadratic trinomial (it does not matter whether it is burdened with additional parameters or not), always try to factor it.
Nuances of the solution
Remember the basic rules for converting rational expressions:
- All denominators and numerators must be factored either through abbreviated multiplication formulas or through a discriminant.
- You need to work according to the following algorithm: when we look and try to isolate the formula for abbreviated multiplication, then, first of all, we try to convert everything to the highest possible degree. After this, we take the overall degree out of the bracket.
- Very often you will encounter expressions with a parameter: other variables will appear as coefficients. We find them using the quadratic expansion formula.
So, once you see rational fractions, the first thing to do is factor both the numerator and denominator into linear expressions, using the abbreviated multiplication or discriminant formulas.
Let's look at a couple of these rational expressions and try to factor them.
Solving more complex examples
Task No. 1
\[\frac(4((x)^(2))-6xy+9((y)^(2)))(2x-3y)\cdot \frac(9((y)^(2))- 4((x)^(2)))(8((x)^(3))+27((y)^(3)))\]
We rewrite and try to decompose each term:
Let's rewrite our entire rational expression taking into account these facts:
\[\frac(((\left(2x \right))^(2))-2x\cdot 3y+((\left(3y \right))^(2)))(2x-3y)\cdot \frac (((\left(3y \right))^(2))-((\left(2x \right))^(2)))(((\left(2x \right))^(3))+ ((\left(3y \right))^(3)))=\]
\[=\frac(((\left(2x \right))^(2))-2x\cdot 3y+((\left(3y \right))^(2)))(2x-3y)\cdot \ frac(\left(3y-2x \right)\left(3y+2x \right))(\left(2x+3y \right)\left(((\left(2x \right))^(2))- 2x\cdot 3y+((\left(3y \right))^(2)) \right))=-1\]
Answer: $-1$.
Problem No. 2
\[\frac(3-6x)(2((x)^(2))+4x+8)\cdot \frac(2x+1)(((x)^(2))+4-4x)\ cdot \frac(8-((x)^(3)))(4((x)^(2))-1)\]
Let's look at all the fractions.
\[((x)^(2))+4-4x=((x)^(2))-4x+2=((x)^(2))-2\cdot 2x+((2)^( 2))=((\left(x-2 \right))^(2))\]
Let's rewrite the entire structure taking into account the changes:
\[\frac(3\left(1-2x \right))(2\left(((x)^(2))+2x+((2)^(2)) \right))\cdot \frac( 2x+1)(((\left(x-2 \right))^(2)))\cdot \frac(\left(2-x \right)\left(((2)^(2))+ 2x+((x)^(2)) \right))(\left(2x-1 \right)\left(2x+1 \right))=\]
\[=\frac(3\cdot \left(-1 \right))(2\cdot \left(x-2 \right)\cdot \left(-1 \right))=\frac(3)(2 \left(x-2 \right))\]
Answer: $\frac(3)(2\left(x-2 \right))$.
Nuances of the solution
So what we just learned:
- Not every square trinomial can be factorized; in particular, this applies to the incomplete square of the sum or difference, which are very often found as parts of sum or difference cubes.
- Constants, i.e. ordinary numbers that do not have variables can also act as active elements in the expansion process. Firstly, they can be taken out of brackets, and secondly, the constants themselves can be represented in the form of powers.
- Very often, after factoring all the elements, opposite constructions arise. These fractions must be reduced extremely carefully, because when crossing them out either above or below, an additional factor $-1$ appears - this is precisely a consequence of the fact that they are opposites.
Solving complex problems
\[\frac(27((a)^(3))-64((b)^(3)))(((b)^(2))-4):\frac(9((a)^ (2))+12ab+16((b)^(2)))(((b)^(2))+4b+4)\]
Let's consider each term separately.
First fraction:
\[((\left(3a \right))^(3))-((\left(4b \right))^(3))=\left(3a-4b \right)\left(((\left (3a \right))^(2))+3a\cdot 4b+((\left(4b \right))^(2)) \right)\]
\[((b)^(2))-((2)^(2))=\left(b-2 \right)\left(b+2 \right)\]
We can rewrite the entire numerator of the second fraction as follows:
\[((\left(3a \right))^(2))+3a\cdot 4b+((\left(4b \right))^(2))\]
Now let's look at the denominator:
\[((b)^(2))+4b+4=((b)^(2))+2\cdot 2b+((2)^(2))=((\left(b+2 \right ))^(2))\]
Let's rewrite the entire rational expression taking into account the above facts:
\[\frac(\left(3a-4b \right)\left(((\left(3a \right))^(2))+3a\cdot 4b+((\left(4b \right))^(2 )) \right))(\left(b-2 \right)\left(b+2 \right))\cdot \frac(((\left(b+2 \right))^(2)))( ((\left(3a \right))^(2))+3a\cdot 4b+((\left(4b \right))^(2)))=\]
\[=\frac(\left(3a-4b \right)\left(b+2 \right))(\left(b-2 \right))\]
Answer: $\frac(\left(3a-4b \right)\left(b+2 \right))(\left(b-2 \right))$.
Nuances of the solution
As we have seen once again, incomplete squares of the sum or incomplete squares of the difference, which are often found in real rational expressions, however, do not be afraid of them, because after transforming each element they are almost always canceled. In addition, in no case should you be afraid of large constructions in the final answer - it is quite possible that this is not your mistake (especially if everything is factorized), but the author intended such an answer.
In conclusion, I would like to look at another complex example, which no longer directly relates to rational fractions, but it contains everything that awaits you on real tests and exams, namely: factorization, reduction to a common denominator, reduction of similar terms. This is exactly what we will do now.
Solving a complex problem of simplifying and transforming rational expressions
\[\left(\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3) )-8)-\frac(1)(x-2) \right)\cdot \left(\frac(((x)^(2)))(((x)^(2))-4)- \frac(2)(2-x) \right)\]
First, let's look at and open the first bracket: in it we see three separate fractions with different denominators, so the first thing we need to do is bring all three fractions to a common denominator, and to do this, each of them should be factored:
\[((x)^(2))+2x+4=((x)^(2))+2\cdot x+((2)^(2))\]
\[((x)^(2))-8=((x)^(3))-((2)^(2))=\left(x-2 \right)\left(((x) ^(2))+2x+((2)^(2)) \right)\]
Let's rewrite our entire construction as follows:
\[\frac(x)(((x)^(2))+2x+((2)^(2)))+\frac(((x)^(2))+8)(\left(x -2 \right)\left(((x)^(2))+2x+((2)^(2)) \right))-\frac(1)(x-2)=\]
\[=\frac(x\left(x-2 \right)+((x)^(3))+8-\left(((x)^(2))+2x+((2)^(2 )) \right))(\left(x-2 \right)\left(((x)^(2))+2x+((2)^(2)) \right))=\]
\[=\frac(((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\left(x-2 \right)\left(((x)^(2))+2x+((2)^(2)) \right))=\frac(((x)^(2))-4x-4)(\ left(x-2 \right)\left(((x)^(2))+2x+((2)^(2)) \right))=\]
\[=\frac(((\left(x-2 \right))^(2)))(\left(x-2 \right)\left(((x)^(2))+2x+(( 2)^(2)) \right))=\frac(x-2)(((x)^(2))+2x+4)\]
This is the result of the calculations from the first bracket.
Let's deal with the second bracket:
\[((x)^(2))-4=((x)^(2))-((2)^(2))=\left(x-2 \right)\left(x+2 \ right)\]
Let's rewrite the second bracket taking into account the changes:
\[\frac(((x)^(2)))(\left(x-2 \right)\left(x+2 \right))+\frac(2)(x-2)=\frac( ((x)^(2))+2\left(x+2 \right))(\left(x-2 \right)\left(x+2 \right))=\frac(((x)^ (2))+2x+4)(\left(x-2 \right)\left(x+2 \right))\]
Now let's write down the entire original construction:
\[\frac(x-2)(((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2 \right)\left(x+2 \right))=\frac(1)(x+2)\]
Answer: $\frac(1)(x+2)$.
Nuances of the solution
As you can see, the answer turned out to be quite reasonable. However, please note: very often during such large-scale calculations, when the only variable appears only in the denominator, students forget that this is the denominator and it should be at the bottom of the fraction and write this expression in the numerator - this is a gross mistake.
In addition, I would like to draw your special attention to how such tasks are formalized. In any complex calculations, all steps are performed one by one: first we count the first bracket separately, then the second one separately, and only at the end do we combine all the parts and calculate the result. In this way, we insure ourselves against stupid mistakes, carefully write down all the calculations and at the same time do not waste any extra time, as it might seem at first glance.
You will need
- - the concept of a monomial of a polynomial;
- - abbreviated multiplication formulas;
- - operations with fractions;
- - basic trigonometric identities.
Instructions
If the expression contains monomials with , find the sum of their coefficients and multiply by the same factor for them. For example, if there is an expression 2 a-4 a+5 a+a=(2-4+5+1)∙a=4∙a.
If the expression is a natural fraction, select the common factor from the numerator and denominator and reduce the fraction by it. For example, if you need to reduce the fraction (3 a²-6 a b+3 b²)/(6∙a²-6∙b²), remove the common factors from the numerator and denominator in the numerator it will be 3, in the denominator 6. Get the expression (3 ( a²-2 a b+b²))/(6∙(a²-b²)). Reduce the numerator and denominator by 3 and apply the abbreviated multiplication formulas to the remaining expressions. For the numerator it is the square of the difference, and for the denominator it is the difference of squares. Get the expression (a-b)²/(2∙ (a+b)∙(a-b)) by reducing it by the common factor a-b, you get the expression (a-b)/(2∙ (a+b)), which is much easier for specific values of the variables count.
If monomials have identical factors raised to a power, then when summing them, make sure that the powers are equal, otherwise it is impossible to reduce similar ones. For example, if there is an expression 2∙m²+6 m³-m²-4 m³+7, then when similar ones are combined, the result will be m²+2 m³+7.
When simplifying trigonometric identities, use formulas to convert them. Basic trigonometric identity sin²(x)+cos²(x)=1, sin(x)/cos(x)=tg(x), 1/ tg(x)= ctg(x), formulas for the sum and difference of arguments, double, triple argument and others. For example, (sin(2∙x)- cos(x))/ ctg(x). Write down the formula for double argument and cotangent as the ratio of cosine to sine. Get (2∙ sin(x) cos(x)- cos(x)) sin(x)/cos(x). Take out the common factor, cos(x) and cancel the fraction cos(x) (2∙ sin(x) - 1) sin(x)/cos(x)= (2∙ sin(x) - 1) sin(x).
Video on the topic
Sources:
- expression simplification formula
Brevity, as they say, is the sister of talent. Everyone wants to show off their talent, but his sister is a complicated thing. For some reason, brilliant thoughts naturally take the form of complex sentences with many adverbial phrases. However, it is up to you to simplify your sentences and make them understandable and accessible to everyone.
Instructions
To make it easier for the recipient (whether listener or reader), try to replace participial and participial phrases with short subordinate clauses, especially if there are too many of the above phrases in one sentence. “A cat who came home, having just eaten a mouse, purred loudly, caressed his owner, trying to look into his eyes, hoping to beg for fish brought from the store” - this will not work. Break such a structure into several parts, take your time and don’t try to say everything in one sentence, you’ll be happy.
If you have conceived a brilliant statement, but it turns out to have too many subordinate clauses (especially with one), then it is better to break the statement into several separate sentences or omit some element. “We decided that he would tell Marina Vasilievna, that Katya would tell Vita that...” - we can continue endlessly. Stop in time and remember who will read or listen to this.
However, the pitfalls lie not only in the structure of the sentence. Pay attention to the vocabulary. Foreign words, long terms, words taken from 19th century fiction - all this will only complicate perception. It is necessary to clarify for yourself for which audience you are composing the text: techies, of course, will understand both complex terms and specific words; but if you offer the same words to a literature teacher, she is unlikely to understand you.
Talent is a great thing. If you are talented (and there are no people without abilities), many roads open up before you. But talent lies not in complexity, but in simplicity, oddly enough. Keep it simple, and your talents will be clear and accessible to everyone.
Video on the topic
Learning to simplify expressions in mathematics is simply necessary in order to correctly and quickly solve problems and various equations. Simplifying an expression involves reducing the number of steps, which makes calculations easier and saves time.

Instructions
Learn to calculate powers of c. When multiplying powers c, a number is obtained whose base is the same, and the exponents are added b^m+b^n=b^(m+n). When dividing powers with the same bases, the power of a number is obtained, the base of which remains the same, and the exponents of the powers are subtracted, and the exponent of the divisor b^m is subtracted from the exponent of the dividend: b^n=b^(m-n). When raising a power to a power, the power of a number is obtained, the base of which remains the same, and the exponents are multiplied (b^m)^n=b^(mn) When raising to a power, each factor is raised to this power. (abc)^m=a^m *b^m*c^m
Factor polynomials, i.e. imagine them as a product of several factors - polynomials and monomials. Take the common factor out of brackets. Learn the basic abbreviated multiplication formulas: difference of squares, squared sum, squared difference, sum of cubes, difference of cubes, cube of sum and difference. For example, m^8+2*m^4*n^4+n^8=(m^4)^2+2*m^4*n^4+(n^4)^2. These formulas are the main ones in simplifying expressions. Use the method of isolating a perfect square in a trinomial of the form ax^2+bx+c.
Abbreviate fractions as often as possible. For example, (2*a^2*b)/(a^2*b*c)=2/(a*c). But remember that you can only reduce multipliers. If the numerator and denominator of an algebraic fraction are multiplied by the same number other than zero, then the value of the fraction will not change. There are two ways to transform rational expressions: by chain and by actions. The second method is preferable, because it is easier to check the results of intermediate actions.
It is often necessary to extract roots in expressions. Even roots are extracted only from non-negative expressions or numbers. Odd roots can be extracted from any expression.
Sources:
- simplification of expressions with powers
An “expression” in mathematics usually refers to a set of arithmetic and algebraic operations involving numbers and variable values. By analogy with the format of writing numbers, such a set is called “fractional” in the case when it contains the division operation. Simplification operations apply to fractional expressions, as well as to numbers in fraction format.

Instructions
Start by finding the common factor for , standing in the numerator and - this is the same for both numerical ratios and those containing unknown variables. For example, if the numerator is 45*X and the denominator is 18*Y, then the greatest common factor is 9. After completing this step, the numerator can be written as 9*5*X and the denominator as 9*2*Y.
If the expressions in the numerator and denominator contain a combination of basic mathematical operations (, division, addition and subtraction), then you will first have to factor out the common factor for each of them separately, and then isolate the greatest common factor from these numbers. For example, for the expression 45*X+180, which is in the numerator, the factor 45 should be taken out of brackets: 45*X+180 = 45*(X+4). And the expression 18+54*Y in the denominator must be reduced to the form 18*(1+3*Y). Then, as in the previous step, find the greatest common divisor of the factors taken out of brackets: 45*X+180 / 18+54*Y = 45*(X+4) / 18*(1+3*Y) = 9*5* (X+4) / 9*2*(1+3*Y). In this example it is also equal to nine.
Reduce the common factor of the expressions in the numerator and denominator of the fraction found in the previous steps. For the example from the first step, the entire simplification operation can be written as follows: 45*X / 18*Y = 9*5*X / 9*2*Y = 5*X / 2*Y.
When simplifying, the common divisor being reduced does not have to be a number; it can also be an expression containing a variable. For example, if the numerator of a fraction is (4*X + X*Y + 12 + 3*Y), and the denominator is (X*Y + 3*Y - 7*X - 21), then the greatest common divisor will be the expression X+ 3, which should be reduced to simplify the expression: (4*X + X*Y + 12 + 3*Y) / (X*Y + 3*Y - 7*X - 21) = (X+3)*(4 +Y) / (X+3)*(Y-7) = (4+Y) / (Y-7).
Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government bodies in the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.
 Symbols of chemical elements and principles of their designation
Symbols of chemical elements and principles of their designation Converting Expressions
Converting Expressions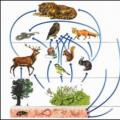 Section IV Biotic connections in nature conclusion
Section IV Biotic connections in nature conclusion