Рациональное уравнение с двумя неизвестными. Рациональные уравнения — Гипермаркет знаний. Решение рациональных уравнений
При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения. Квадрат суммы:
Квадрат разности:
Предыдущие две формулы также иногда записывают в несколько другом виде, который даёт нам какое-то выражение для суммы квадратов:

Также нужно понимать, что будет получаться если в скобках в квадрате знаки будут расставлены "нестандартным" способом:

Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и квадратный трехчлен
Пусть квадратное уравнение имеет вид:
Тогда дискриминант находят по формуле:
![]()
Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле :

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле :
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле :
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой :
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета . Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Основные свойства степеней
У математических степеней есть несколько важных свойств, перечислим их. При умножении степеней с одинаковыми основаниями показатели степеней складываются:
![]()
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель степени делителя:
При возведении степени в степень показатели степеней перемножаются:
![]()
Если перемножаются числа с одинаковой степенью, но разным основанием, то можно сначала перемножить числа, а затем произведение возвести в эту степень. Обратная процедура также возможна, если имеется произведение в степени, то можно каждое из умножаемых возвести в эту степень по отдельности а результаты перемножить:
![]()
Также, если делятся числа с одинаковой степенью, но разным основанием, то можно сначала поделить числа, а затем частное возвести в эту степень (обратная процедура также возможна):
Несколько простых свойств степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:

Основные свойства математических корней
Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:
![]()
Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:
![]()
![]()
Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):
Последнее справедливо: если n – нечетное, то для любого a ; если же n – четное, то только при неотрицательном a . Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак "минус"):
![]()
Так как значение корня четной степени может быть только неотрицательным , то для таких корней имеется следующее важное свойство:

Некоторые дополнительные сведения из алгебры
Если x 0 – корень многочлена n -ой степени P n (x ), то выполняется следующее равенство (здесь Q n-1 (x ) – некоторый многочлен (n – 1)-ой степени):
Процедура в рамках которой квадратный трехчлен представляется как скобка в квадрате и еще некоторое слагаемое называется выделением полного квадрата . И хотя операцию выделения полного квадрата проще выполнять каждый раз "с ноля" в конкретных цифрах, тем не менее имеется и общая формула, с помощью которой можно записывать сразу результат выделения полного квадрата:

Существует операция, обратная операции сложения дробей с одинаковыми знаменателями, и которая называется почленным делением . Она заключается в том, чтобы наоборот каждое слагаемое из суммы в числителе некоторой дроби, записать отдельно над знаменателем этой дроби. Для операции почленного деления также можно записать общую формулу:
Существует также формула для разложения суммы квадратов на множители :
Решение рациональных уравнений
Решить уравнение – значит найти все его корни. Основной метод решения – путем алгебраических преобразований или замены переменных свести уравнение к равносильному, которое решается просто (например, к квадратному). Если свести уравнение к равносильному не получается, то могут возникать побочные корни. Сомневаетесь – проверяйте корни подстановкой.
Для многих уравнений важно понятие области допустимых значений для корней, далее – ОДЗ. На данном этапе (в рациональных уравнениях, т.е. тех, которые не содержат арифметических корней, тригонометрических функций, логарифмов и т.д.), основное условие которому должны отвечать корни уравнения, это чтобы при их подстановке в изначальный вид уравнения знаменатели дробей не обращались в ноль, т.к. на ноль делить нельзя. Таким образом, ОДЗ включает все возможные значения кроме тех которые обращают в ноль знаменатели дробей.
При решении уравнений (а в дальнейшем и неравенств) нельзя сокращать множители с переменной в левой и правой части уравнения (неравенства), в этом случае Вы потеряете корни. Нужно переносить все выражения налево от знака равно и выносить "сокращающийся" множитель за скобки, в дальнейшем нужно учесть корни, которые он дает.
Для того чтобы произведение двух или более скобок было равно нулю, достаточно чтобы любая из них по отдельности была равна нулю, а остальные существовали. Поэтому в таких случаях нужно по очереди приравнивать все скобки к нулю. В итоговый ответ нужно записать корни всех этих "веток" решения (если конечно эти корни входят в ОДЗ).
Иногда некоторые из дробей в рациональном уравнении можно сократить. Это нужно обязательно попытаться сделать и не упустить ни одной такой возможности. Но при сокращении дроби Вы можете потерять ОДЗ, поэтому дроби нужно сокращать только после записи ОДЗ, или же в конце решения полученные корни подставлять в первоначальное уравнение для проверки существования знаменателей.
Итак, для решения рационального уравнения необходимо:
- Разложить все знаменатели всех дробей на множители.
- Перенести все слагаемые влево, чтобы справа получился ноль.
- Записать ОДЗ.
- Сократить дроби, если это возможно.
- Привести к общему знаменателю.
- Упростить выражение в числителе.
- Приравнять числитель к нулю и решать полученное уравнение.
- Не забыть проверить корни на соответствие ОДЗ.
Одним из самых распространённых методов решения уравнений является метод замены переменных . Зачастую замена переменных выбирается индивидуально для каждого конкретного примера. При этом важно помнить о двух основных критериях введения замены в уравнения. Итак после введения замены в некоторое уравнение это уравнение должно:
- во-первых, стать проще;
- во-вторых, больше не содержать первоначальной переменной.
Кроме того, важно не забывать выполнять обратную замену, т.е. после нахождения значений для новой переменной (для замены), записывать вместо замены то, чему она равна через первоначальную переменную, приравнивать это выражение к найденным значениям для замены и опять решать уравнения.
Отдельно остановимся на алгоритме решения очень распространённых однородных уравнений . Однородные уравнения имеют вид:
Здесь А, В и С – числа, не равные нулю, а f (x ) и g (x ) – некоторые функции с переменной х . Однородные уравнения решают так: разделим все уравнение на g 2 (x ) и получим:

Производим замену переменных:
И решаем квадратное уравнение:
Получив корни этого уравнения не забываем выполнить обратную замену, а также проверить корни на соответствие ОДЗ.
Также при решении некоторых рациональных уравнений хорошо бы помнить про следующие полезные преобразования:

Решение систем рациональных уравнений
Решить систему уравнений – значит найти не просто решение, а комплекты решений, то есть такие значения всех переменных которые, будучи одновременно подставленными в систему, обращают каждое ее уравнение в тождество. При решении систем уравнений можно применять следующие методы (про ОДЗ при этом не забываем):
- Метод подстановки. Метод состоит в том, чтобы выразив одну из переменных из одного из уравнений, подставить это выражение вместо данной неизвестной в остальные уравнения, уменьшив таким образом количество неизвестных в оставшихся уравнениях. Данная процедура повторяется пока не останется одно уравнение с одной переменной, которое затем и решается. Остальные неизвестные последовательно находятся по уже известным значениям найденных переменных.
- Метод расщепления системы. Этот метод состоит в том, чтобы разложить одно из уравнений системы на множители. При этом необходимо чтобы справа в этом уравнении был ноль. Тогда приравнивая по очереди каждый множитель этого уравнения к нолю и дописывая остальные уравнения первоначальной системы, получим несколько систем, но каждая из них будет проще первоначальной.
- Метод сложения и вычитания. Данный метод состоит в том, чтобы складывая либо вычитая два уравнения системы (их предварительно можно и часто нужно умножать на некоторый коэффициент) получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.
- Метод деления и умножения. Данный метод состоит в том, чтобы разделив либо умножив соответственно левые и правые части двух уравнений системы получить новое уравнение, и заменить им одно из уравнений первоначальной системы. Очевидно, что такая процедура опять таки имеет смысл, только если новое уравнение будет получаться значительно проще ранее имевшихся.
Существуют и другие методы решения систем рациональных уравнений. В числе которых - замена переменных . Зачастую замена переменных подбирается индивидуально под каждый конкретный пример. Но есть два случая, где всегда нужно вводить совершенно определённую замену. Первый из этих случаев, это случай когда оба уравнения системы с двумя неизвестными являются однородными многочленами приравненными к некоторому числу. В этом случае нужно использовать замену:
После применения этой замены, к слову, нужно будет для продолжения решения таких систем использовать метод деления. Второй случай, это симметричные системы с двумя переменными, т.е. такие системы, которые не изменяются при замене x на y , а y на x . В таких системах необходимо применять следующую двойную замену переменных:
При этом, для того чтобы ввести такую замену в симметричную систему, первоначальные уравнения скорее всего придется сильно преобразовывать. Про ОДЗ и обязательность выполнения обратной замены в обоих этих методах, конечно нельзя забывать.
- Назад
- Вперёд
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Наименьший общий знаменатель используется для упрощения данного уравнения. Этот метод применяется в том случае, когда вы не можете записать данное уравнение с одним рациональным выражением на каждой стороне уравнения (и воспользоваться методом умножения крест-накрест). Этот метод используется, когда вам дано рациональное уравнение с 3 или более дробями (в случае двух дробей лучше применить умножение крест-накрест).
Найдите наименьший общий знаменатель дробей (или наименьшее общее кратное). НОЗ – это наименьшее число, которое делится нацело на каждый знаменатель.
- Иногда НОЗ – очевидное число. Например, если дано уравнение: х/3 + 1/2 = (3x +1)/6, то очевидно, что наименьшим общим кратным для чисел 3, 2 и 6 будет 6.
- Если НОЗ не очевиден, выпишите кратные самого большого знаменателя и найдите среди них такой, который будет кратным и для других знаменателей. Зачастую НОЗ можно найти, просто перемножив два знаменателя. Например, если дано уравнение x/8 + 2/6 = (x - 3)/9, то НОЗ = 8*9 = 72.
- Если один или несколько знаменателей содержат переменную, то процесс несколько усложняется (но не становится невозможным). В этом случае НОЗ представляет собой выражение (содержащее переменную), которое делится на каждый знаменатель. Например, в уравнении 5/(х-1) = 1/х + 2/(3x) НОЗ = 3x(х-1), потому что это выражение делится на каждый знаменатель: 3x(х-1)/(х-1) = 3x; 3x(х-1)/3х = (х-1); 3x(х-1)/х = 3(х-1).
Умножьте и числитель, и знаменатель каждой дроби на число, равное результату деления НОЗ на соответствующий знаменатель каждой дроби. Так как вы умножаете и числитель, и знаменатель на одно и тоже число, то фактически вы умножаете дробь на 1 (например, 2/2 = 1 или 3/3 = 1).
- Таким образом, в нашем примере умножьте х/3 на 2/2, чтобы получить 2x/6, и 1/2 умножьте на 3/3, чтобы получить 3/6 (дробь 3x +1/6 умножать не надо, так как ее знаменатель равен 6).
- Действуйте аналогично в случае, когда переменная находится в знаменателе. В нашем втором примере НОЗ = 3x(x-1), поэтому 5/(x-1) умножьте на (3x)/(3x) и получите 5(3x)/(3x)(x-1); 1/x умножьте на 3(x-1)/3(x-1) и получите 3(x-1)/3x(x-1); 2/(3x) умножьте на (x-1)/(x-1) и получите 2(x-1)/3x(x-1).
Найдите х. Теперь, когда вы привели дроби к общему знаменателю, вы можете избавиться от знаменателя. Для этого умножьте каждую сторону уравнения на общий знаменатель. Затем решите полученное уравнение, то есть найдите «х». Для этого обособьте переменную на одной из сторон уравнения.
- В нашем примере: 2x/6 + 3/6 = (3x +1)/6. Вы можете сложить 2 дроби с одинаковым знаменателем, поэтому запишите уравнение как: (2x+3)/6=(3x+1)/6. Умножьте обе части уравнения на 6 и избавьтесь от знаменателей: 2x+3 = 3x +1. Решите и получите х = 2.
- В нашем втором примере (с переменной в знаменателе) уравнение имеет вид (после приведения к общему знаменателю): 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). Умножив обе стороны уравнения на НОЗ, вы избавитесь от знаменателя и получите: 5(3x) = 3(х-1) + 2(х-1), или 15x = 3x - 3 + 2x -2, или 15х = х - 5. Решите и получите: х = -5/14.
Обращение автора к данной теме не является случайным. Уравнения с двумя переменными впервые встречаются в курсе 7-го класса. Одно уравнение с двумя переменными имеет бесконечное множество решений. Это наглядно демонстрирует график линейной функции, заданный в виде ax + by=c. В школьном курсе учащиеся изучают системы двух уравнений с двумя переменными. В результате из поля зрения учителя и, поэтому ученика, выпадает целый ряд задач, с ограниченными условиями на коэффициент уравнения, а также методы их решения.
Речь идет о решении уравнения с двумя неизвестными в целых или натуральных числах.
В школе натуральные и целые числа изучаются в 4-6-х классах. К моменту окончания школы не все ученики помнят различия между множествами этих чисел.
Однако задача типа “решить уравнение вида ax + by=c в целых числах” все чаще встречается на вступительных экзаменах в ВУЗы и в материалах ЕГЭ.
Решение неопределенных уравнений развивает логическое мышление, сообразительность, внимание анализировать.
Я предлагаю разработку нескольких уроков по данной теме. У меня нет однозначных рекомендаций по срокам проведения этих уроков. Отдельные элементы можно использовать и в 7-м классе (для сильного класса). Данные уроки можно взять за основу и разработать небольшой элективный курс по предпрофильной подготовке в 9-м классе. И, конечно, этот материал можно использовать в 10-11 классах для подготовки к экзаменам.
Цель урока:
- повторение и обобщение знаний по теме “Уравнения первого и второго порядка”
- воспитание познавательного интереса к учебному предмету
- формирование умений анализировать, проводить обобщения, переносить знания в новую ситуацию
Урок 1.
Ход урока.
1) Орг. момент.
2) Актуализация опорных знаний.
Определение. Линейным уравнением с двумя переменными называется уравнение вида
mx + ny = k, где m, n, k – числа, x, y – переменные.
Пример: 5x+2y=10
Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.
1. 5x+2y=12 (2)y = -2.5x+6
Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.
Пусть x = 2, y = -2.5 2+6 = 1
x = 4, y = -2.5 4+6 =- 4
Пары чисел (2;1); (4;-4) – решения уравнения (1).
Данное уравнение имеет бесконечно много решений.
3) Историческая справка
Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.
В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.
Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.
4) Изучение нового материала.
Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y Z k0
Утверждение 1.
Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Пример: 34x – 17y = 3.
НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.
Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.
Утверждение 2.
Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Утверждение 3.
Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:
Где (; ) – какое-либо решение уравнения (1), t Z
Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)
Утверждение 4.
Если m и n – взаимно простые числа, то всякое
решение уравнения (2) имеет вид ![]()
5) Домашнее задание. Решить уравнение в целых числах:
- 9x – 18y = 5
- x + y= xy
- Несколько детей собирали яблоки. Каждый мальчик собрал по 21 кг, а девочка по 15 кг. Всего они собрали 174 кг. Сколько мальчиков и сколько девочек собирали яблоки?
Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.
Урок 2.
1) Организационный момент
2) Проверка домашнего задания
1) 9x – 18y = 5
5 не делится нацело на 9, в целых числах решений нет.
Методом подбора можно найти решение
Ответ: (0;0), (2;2)
3) Составим уравнение:
Пусть мальчиков x, x Z, а девочек у, y Z, то можно составить уравнение 21x + 15y = 174
Многие учащиеся, составив уравнение, не смогут его решить.
Ответ: мальчиков 4, девочек 6.
3) Изучение нового материала
Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.
I. Метод рассмотрения остатков от деления.
Пример. Решить уравнение в целых числах 3x – 4y = 1.
Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.
Ответ: где m Z.
Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.
Пример: Решить уравнения в целых числах.
Пусть y = 4n, тогда 16 - 7y = 16 – 7 4n = 16 – 28n = 4*(4-7n) делится на 4.
y = 4n+1, тогда 16 – 7y = 16 – 7 (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.
y = 4n+2, тогда 16 – 7y = 16 – 7 (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.
y = 4n+3, тогда 16 – 7y = 16 – 7 (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.
Следовательно, y = 4n, тогда
4x = 16 – 7 4n = 16 – 28n, x = 4 – 7n
Ответ: , где n Z.
II. Неопределенные уравнения 2-ой степени
Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.
И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.
Пример: Решить уравнение в целых числах.
![]()
13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13 1 = 1 13 = (-1)(-13) = (-13)(-1)
Рассмотрим эти случаи
Ответ: (7;-3), (7;3), (-7;3), (-7;-3).
4) Домашнее задание.
Примеры. Решить уравнение в целых числах:
(x - y)(x + y)=4
| 2x = 4 | 2x = 5 | 2x = 5 |
| x = 2 | x = 5/2 | x = 5/2 |
| y = 0 | не подходит | не подходит |
| 2x = -4 | не подходит | не подходит |
| x = -2 | ||
| y = 0 |
Ответ: (-2;0), (2;0).
Ответы: (-10;9), (-5;3), (-2;-3), (-1;-9), (1;9), (2;3), (5;-3), (10;-9).
в) ![]()
Ответ: (2;-3), (-1;-1), (-4;0), (2;2), (-1;3), (-4;5).
Итоги. Чтозначит решить уравнение в целых числах?
Какие методы решения неопределенных уравнений вы знаете?
Приложение:
Упражнения для тренировки.
1) Решите в целых числах.
| а) 8x + 12y = 32 | x = 1 + 3n, y = 2 - 2n, n Z |
| б) 7x + 5y = 29 | x = 2 + 5n, y = 3 – 7n, n Z |
| в) 4x + 7y = 75 | x = 3 + 7n, y = 9 – 4n, n Z |
| г) 9x – 2y = 1 | x = 1 – 2m, y = 4 + 9m, m Z |
| д) 9x – 11y = 36 | x = 4 + 11n, y = 9n, n Z |
| е) 7x – 4y = 29 | x = 3 + 4n, y = -2 + 7n, n Z |
| ж) 19x – 5y = 119 | x = 1 + 5p, y = -20 + 19p, p Z |
| з) 28x – 40y = 60 | x = 45 + 10t, y = 30 + 7t, t Z |
2) Найти целые неотрицательные решения уравнения:
Решение:Z (2; -1)
Литература.
- Детская энциклопедия “Педагогика”, Москва, 1972 г.
- Алгебра-8, Н.Я. Виленкин, ВО “Наука”, Новосибирск, 1992 г.
- Конкурсные задачи, основанные на теории чисел. В.Я. Галкин, Д.Ю. Сычугов. МГУ, ВМК, Москва, 2005г.
- Задачи повышенной трудности в курсе алгебры 7-9 классов. Н.П. Косрыкина. “Просвещение”, Москва, 1991 г.
- Алгебра 7, Макарычев Ю.Н., “Просвещение”.
Конспект урока по математике
на тему:
« Рациональные уравнения с двумя переменными.
Основные понятия ».
Подготовила:
Учитель математики
МБОУ СОШ №2
Борщова Е. С.
Павловский Посад
Тип урока : изучение нового материала.
Тема урока : рациональные уравнения с двумя переменными. Основные понятия.
Цели :
ввести основные понятия и термины темы;
развивать математическую речь и мышление учащихся.
Оборудование: доска для записей, проектор, экран, презентация.
Организационный момент. (2 – 3 мин.)
(1 слайд)
Здравствуйте, ребята, присаживайтесь! Сегодня мы с вами рассмотрим новую, достаточно интересную тему, которая станет залогом к успешному усвоению будущего материала. Открываем рабочие тетради, записываем число, сегодня 16 октября, классная работа и тему урока: «Рациональные уравнения с двумя переменными. Основные понятия». (учитель тоже самое записывает на доске)
II . Актуализация знаний. (5 мин.)
(2 слайд)
Для того, чтобы начать изучение новой темы нам необходимо вспомнить некоторый материал, который вы уже знаете. Итак, вспомним элементарные функции и их графики:
1. График линейной функции

2. Парабола. График квадратичной функции
![]() , (а ≠ 0)
, (а ≠ 0)
Рассмотрим канонический случай:

3. Кубическая парабола
Кубическая парабола задается функцией

4. График гиперболы
Опять же вспоминаем тривиальную гиперболу

Очень хорошо!
III . Изучение нового материала (сопровождается презентацией). (35 мин.)
(3 слайд)
На предыдущих уроках вы выучили определение рационального уравнения с одной переменной, и сейчас мы говорим, что оно очень схоже с определением рационального уравнения с двумя переменными:
Его записывать не нужно, оно есть в ваших учебниках, еще раз прочитаете его дома и выучите!
А в тетради запишите примеры:

Далее можно сказать, что рациональное уравнение вида h(x; y) = g(x; y) всегда можно преобразовать к виду p(x; y) = 0, где p(x; y) = 0 – рациональное выражение. Для этого нужно переписать выражение так: h (x ; y ) - g (x ; y ) = 0, т. е. p (x ; y ) = 0. последние два равенства запишите себе в тетради!
(4 слайд)
Следующее определение внимательно слушаем и запоминаем, записывать его не нужно!
А в тетради запишите только примеры:
(5 слайд)
Решим такое уравнение (учащиеся записывают решение в тетради, учитель комментирует каждый шаг решения, параллельно отвечая на вопросы детей):

(6 слайд)
Следующее определение, это определение равносильности двух уравнение, его вы тоже уже знаете из предыдущих параграфов, поэтому просто смотрим и слушаем:
Теперь давайте вспомним, какие вы знаете равносильные преобразования:
Перенос членов уравнения из одной части в другую с противоположными знаками (примеры на доске, их можете не записывать, кто хочет – запишите);
Умножение или деление обеих частей уравнения на одно и тоже число отличное от нуля или (еще мы знаем) на выражение, всюду отличное от нуля (обратите на это внимание!); (примеры кому нужно запишите).
А какие вы знаете неравносильные преобразования?
1) освобождение от знаменателей, содержащих переменные;
2) возведение обеих частей уравнения в квадрат.
Прекрасно!
(7 слайд)
Следующее понятие, которое мы сегодня рассмотрим, записываем – формула расстояния между двумя точками.
Пишите:

 (учащиеся обе теоремы записывают себе в тетради)
(учащиеся обе теоремы записывают себе в тетради)
 Этот рисунок перерисовываем в тетради, подписываем оси координат, центр окружности, отмечаем радиус.
Этот рисунок перерисовываем в тетради, подписываем оси координат, центр окружности, отмечаем радиус.
Есть ли у вас какие-то вопросы? (если вопросов нет, продолжаем работу)
(8 слайд)
Рассмотрим примеры, записывайте:

 (рис. к П1)
(рис. к П1)  (рис. к П2)
(рис. к П2)
Дети постепенно, исходя их выше записанной теоремы, отвечая на вопросы учителя, самостоятельно решают, записывают решение в тетради, рисунки перерисовывают.
Молодцы! А сейчас, перерисуйте себе такую таблицу, она станет хорошим помощником в дальнейшем при решении задач.
(9 слайд)
 Учащиеся аккуратно, каждый в своих тетрадях рисует данную таблицу и заносит в нее данные.
Учащиеся аккуратно, каждый в своих тетрадях рисует данную таблицу и заносит в нее данные.
V. Домашнее задание (2 – 3 мин.).
(10 слайд)
До конца урока осталось 2 минуты, открываем дневники, записываем домашнее задание:
1) Глава 2, §5;
2) стр. 71 вопросы для самопроверки;
3) № 5.1; № 5.3 (а, б); № 5.7.
Самоанализ.
Начало урока было достаточно доброжелательным, искренним, открытым и организованным. Класс к уроку был подготовлен. Дети в течение всего урока показывали хорошую работоспособность.
Мною сразу были озвучены цели урока. Цели, предложенные детям на урок, соответствовали программным требованиям, содержанию материала.
В начале урока, в качестве активизации познавательной деятельности, детям было предложено вспомнить некоторый материал по ранее изученному материалу, с чем они справились без каких-либо особых затруднений.
Содержание урока соответствовало требованиям образовательного стандарта.
Структура урока предложена выше. На мой взгляд, целям и типу урока она соответствует. Этапы урока были логически связаны, плавно переходили один в другой. На каждом из этапов подводились итоги. Время распределялось на отдельные этапы по-разному в зависимости от того, какой из них являлся основным. На мой взгляд, оно было распределено рационально. Начало и конец урока были организованными. Темп ведения урока был оптимальным.
После первого этапа актуализации знаний шел основной этап урока – объяснение нового материала. Этот этап был главным, поэтому основное время было уделено именно ему.
Изложение нового материала было логичным, грамотным, на высоком теоретическом и одновременно доступном для детей уровне. Главные мысли по теме всегда мной выделялись и записывались учащимися в рабочие тетради.
Изучение нового материала было проведено в форме небольшой лекции с выполнением элементарных практических заданий, для наиболее быстрого и правильного усвоения материала.
Мною была выполнена презентация в программе PowerPoint. Презентация имела в основном вспомогательную функцию.
С целью контроля усвоения знаний на протяжении всего урока учащиеся решали задачи, по результатам чего я могла судить о степени усвоения теоретического материала каждым из детей. После проведения контроля знаний учителем была проведена коррекционная работа. Те вопросы, которые вызвали у учащихся наибольшее затруднение, были рассмотрены еще раз.
После этого был подведен итог урока и ученикам предложено домашнее задание. Домашнее задание было закрепляющего, развивающего характера. На мой взгляд, оно было посильно для всех детей.
Содержание урока было оптимальным, методы обучения – устный, наглядный и практический. Форма работы – беседа. Я использовала приемы активизации познавательной деятельности – это постановка проблемных вопросов, обобщение по планам обобщенного характера.
Учащиеся на уроке были активными. Они показали умение продуктивно работать, делать выводы по увиденному, умение анализировать и обобщать свои знания. Также дети показали наличие навыков самоконтроля, но лишь единицы были неусидчивы, и им уделялось наибольшее внимание с моей стороны.
Класс к уроку был подготовлен.
Я считаю, что цели поставленные в начале урока достигнуты.
В курсе математики 7 класса впервые встречаются с уравнениями с двумя переменными , но изучаются они лишь в контексте систем уравнений с двумя неизвестными. Именно поэтому из поля зрения выпадает целый ряд задач, в которых на коэффициенты уравнения введены некоторые условия, их ограничивающие. Кроме того, остаются без внимания и методы решения задач типа «Решить уравнение в натуральных или целых числах», хотя в материалах ЕГЭ и на вступительных экзаменах задачи такого рода встречаются все чаще и чаще.
Какое уравнение будет называться уравнением с двумя переменными?
Так, например, уравнения 5x + 2y = 10, x 2 + y 2 = 20 или xy = 12 являются уравнениями с двумя переменными.
Рассмотрим уравнение 2x – y = 1. Оно обращается в верное равенство при x = 2 и y = 3, поэтому эта пара значений переменных является решением рассматриваемого уравнения.
Таким образом, решением любого уравнения с двумя переменными является множество упорядоченных пар (x; y), значений переменных, которые это уравнение обращают в верное числовое равенство.
Уравнение с двумя неизвестными может:
а) иметь одно решение. Например, уравнение x 2 + 5y 2 = 0 имеет единственное решение (0; 0);
б) иметь несколько решений. Например, (5 -|x|) 2 + (|y| – 2) 2 = 0 имеет 4 решения: (5; 2), (-5; 2), (5; -2), (-5; -2);
в) не иметь решений. Например, уравнение x 2 + y 2 + 1 = 0 не имеет решений;
г) иметь бесконечно много решений. Например, x + y = 3. Решениями этого уравнения будут являться числа, сумма которых равна 3. Множество решений данного уравнения можно записать в виде (k; 3 – k), где k – любое действительное число.
Основными методами решения уравнений с двумя переменными являются методы, основанные на разложении выражений на множители, выделение полного квадрата, использование свойств квадратного уравнения, ограниченности выражений, оценочные методы. Уравнение, как правило, преобразовывают к виду, из которого можно получить систему для нахождения неизвестных.
Разложение на множители
Пример 1.
Решить уравнение: xy – 2 = 2x – y.
Решение.
Группируем слагаемые с целью разложения на множители:
(xy + y) – (2x + 2) = 0. Из каждой скобки вынесем общий множитель:
y(x + 1) – 2(x + 1) = 0;
(x + 1)(y – 2) = 0. Имеем:
y = 2, x – любое действительное число или x = -1, y – любое действительное число.
Таким образом, ответом являются все пары вида (x; 2), x € R и (-1; y), y € R.
Равенство нулю неотрицательных чисел
Пример 2.
Решить уравнение: 9x 2 + 4y 2 + 13 = 12(x + y).
Решение.
Группируем:
(9x 2 – 12x + 4) + (4y 2 – 12y + 9) = 0. Теперь каждую скобку можно свернуть по формуле квадрата разности.
(3x – 2) 2 + (2y – 3) 2 = 0.
Сумма двух неотрицательных выражений равна нулю, только если 3x – 2 = 0 и 2y – 3 = 0.
А значит, x = 2/3 и y = 3/2.
Ответ: (2/3; 3/2).
Оценочный метод
Пример 3.
Решить уравнение: (x 2 + 2x + 2)(y 2 – 4y + 6) = 2.
Решение.
В каждой скобке выделим полный квадрат:
((x + 1) 2 + 1)((y – 2) 2 + 2) = 2. Оценим  значение выражений, стоящих в скобках.
значение выражений, стоящих в скобках.
(x + 1) 2 + 1 ≥ 1 и (y – 2) 2 + 2 ≥ 2, тогда левая часть уравнения всегда не меньше 2. Равенство возможно, если:
(x + 1) 2 + 1 = 1 и (y – 2) 2 + 2 = 2, а значит x = -1, y = 2.
Ответ: (-1; 2).
Познакомимся с еще одним методом решения уравнений с двумя переменными второй степени. Этот метод заключается в том, что уравнение рассматривается как квадратное относительно какой-либо переменной .
Пример 4.
Решить уравнение: x 2 – 6x + y – 4√y + 13 = 0.
Решение.
Решим уравнение как квадратное относительно x. Найдем дискриминант:
D = 36 – 4(y – 4√y + 13) = -4y + 16√y – 16 = -4(√y – 2) 2 . Уравнение будет иметь решение только при D = 0, т. е. в том случае, если y = 4. Подставляем значение y в исходное уравнение и находим, что x = 3.
Ответ: (3; 4).
Часто в уравнениях с двумя неизвестными указывают ограничения на переменные .
Пример 5.
Решить уравнение в целых числах: x 2 + 5y 2 = 20x + 2.
Решение.
Перепишем уравнение в виде x 2 = -5y 2 + 20x + 2. Правая часть полученного уравнения при делении на 5 дает в остатке 2. Следовательно, x 2 не делится на 5. Но квадрат числа, не делящегося на 5, дает в остатке 1 или 4. Таким образом, равенство невозможно и решений нет.
Ответ: нет корней.
Пример 6.
Решить уравнение: (x 2 – 4|x| + 5)(y 2 + 6y + 12) = 3.
Решение.
Выделим полные квадраты в каждой скобке:
((|x| – 2) 2 + 1)((y + 3) 2 + 3) = 3. Левая часть уравнения всегда больше или равна 3. Равенство возможно при условии |x| – 2 = 0 и y + 3 = 0. Таким образом, x = ± 2, y = -3.
Ответ: (2; -3) и (-2; -3).
Пример 7.
Для каждой пары целых отрицательных чисел (x; y), удовлетворяющих уравнению
x 2 – 2xy + 2y 2 + 4y = 33, вычислить сумму (x + y). В ответе указать наименьшую из сумм.
Решение.
Выделим полные квадраты:
(x 2 – 2xy + y 2) + (y 2 + 4y + 4) = 37;
(x – y) 2 + (y + 2) 2 = 37. Так как x и y – целые числа, то их квадраты также целые числа. Сумму квадратов двух целых чисел, равную 37, получим, если складываем 1 + 36. Следовательно:
(x – y) 2 = 36 и (y + 2) 2 = 1
(x – y) 2 = 1 и (y + 2) 2 = 36.
Решая эти системы и учитывая, что x и y – отрицательные, находим решения: (-7; -1), (-9; -3), (-7; -8), (-9; -8).
Ответ: -17.
Не стоит отчаиваться, если при решении уравнений с двумя неизвестными у вас возникают трудности. Немного практики, и вы сможете справиться с любыми уравнениями.
Остались вопросы? Не знаете, как решать уравнения с двумя переменными?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
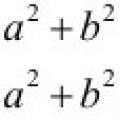 Рациональные уравнения — Гипермаркет знаний
Рациональные уравнения — Гипермаркет знаний Возрастная структура населения мира Какие группы возрастов выделяют в населении земли
Возрастная структура населения мира Какие группы возрастов выделяют в населении земли Формулы сокращенного умножения Сложение алгебраических дробей
Формулы сокращенного умножения Сложение алгебраических дробей