Emme valitse matematiikkaahänen ammatinsa, ja hän valitsee meidät.

Venäläinen matemaatikko yu.i. Manin

Yhtälöt moduulilla

Koulun matematiikan vaikeimmat ratkaistu tehtävät ovat yhtälöitä, jotka sisältävät muuttujia moduulin merkki. Jotta tällaiset yhtälöt onnistuneesti ratkaistaan, on välttämätöntä tietää moduulin määritelmä ja perusominaisuudet. Luonnollisesti opiskelijoille tulisi olla tämäntyyppisten yhtälöiden ratkaiseminen.

Peruskäsitteet ja ominaisuudet

Kelvollisen numeron moduuli (absoluuttinen arvo) merkitsee ja määritellään seuraavasti:

Seuraavissa suhteissa ovat moduulin yksinkertaiset ominaisuudet:

Merkintä että kaksi viimeistä kiinteistöä ovat päteviä mihinkään tutkintoon.

Lisäksi, jos, missä sitten

Moduulin monimutkaisempia ominaisuuksia, jota voidaan tehokkaasti käyttää ratkaistavat yhtälöitä moduuleilla, Seuraamalla seuraavia teoreita:

Teorem 1. Analyyttiset toiminnot ja Melko epätasa-arvo

Teorem 2. Tasa-arvo vastaa eriarvoisuutta.

Teorem 3. Tasa-arvo vastaa epätasa-arvoa.

Harkitse tyypillisiä esimerkkejä aihepiirien ongelmien ratkaisemisesta "yhtälöt, sisältää muuttujia moduulin merkin alla. "

Yhtälöiden ratkaisu moduulilla

Yleisin koulun matematiikassa ratkaisemalla yhtälöt moduulilla on menetelmä, Perustuu moduulien paljastamiseen. Tämä menetelmä on universaali, Yleensä sen käyttö voi johtaa erittäin hankaliin laskelmiin. Tältä osin opiskelijoiden pitäisi tuntea muita, Tehokkaampia menetelmiä ja tekniikoita tällaisten yhtälöiden ratkaisemiseksi. Erityisesti, On välttämätöntä olla taitoja teoreiden käytöstä, tässä artikkelissa.

Esimerkki 1.Ratkaise yhtälö. (yksi)

Päätös. Yhtälö (1) ratkaisee "klassisen" menetelmän moduulien paljastamiseksi. Voit tehdä tämän, rikkomme numeerisen akselin Pisteet I. Välein ja harkitse kolme tapausta.

1. Jos sitten yhtälö (1) on lomakkeen. Täältä seuraa. Tässä kuitenkin, joten löytynyt arvo ei ole yhtälön (1) juuret.

2. Jos, Sitten yhtälöstä (1) saamme Tai.

Siitä lähtien root yhtälö (1).

3. Jos, Että yhtälö (1) ottaa Tai. Ota huomioon, että.

Vastaus :,.

Moduulin myöhempien yhtälöiden ratkaisemisessa käytämme aktiivisesti moduulien ominaisuuksia, jotta voidaan lisätä tällaisten yhtälöiden ratkaisemisen tehokkuutta.

Esimerkki 2. Ratkaise yhtälö.

Päätös. Yhtä hyvin sitten yhtälöstä seuraa. Tässä suhteessa, ,, ja yhtälö vie. Täältä saamme. Mutta , Siksi alkuperäisen juuren yhtälöllä ei ole juuria.

Vastaus: Ei juuria.

Esimerkki 3. Ratkaise yhtälö.

Päätös. Siitä lähtien. Jos sitten ja yhtälö vie.

Täältä saamme.

Esimerkki 4. Ratkaise yhtälö.

Päätös.Kirjoita yhtälö uudelleen vastaavassa muodossa. (2)

Tuloksena oleva yhtälö viittaa tyypin yhtälöihin.

Ottaen huomioon lause 2, voidaan väittää, että yhtälö (2) vastaa eriarvoisuutta. Täältä saamme.

Vastaus:.

Esimerkki 5. Ratkaise yhtälö.

Päätös. Tämä yhtälö on lomake. Siksi , Theoremin 3 mukaan., Täällä meillä on epätasa-arvo Tai.

Esimerkki 6. Ratkaise yhtälö.

Päätös. Laitamme sen. Kuten , Sitten määritetty yhtälö näkyy neliön yhtälöstä, (3)

missä . Koska yhtälöllä (3) on yksi positiivinen juurta Ja tuo . Täältä saamme kaksi juuria alkuperäisestä yhtälöstä: ja.

Esimerkki 7. Ratkaise yhtälö. (4)

Päätös. Yhtälöstä vastaa kahden yhtälön kokonaisuutta: ja Tämä ratkaista samalla yhtälöä (4), on tarpeen tarkastella kahta tapausta.

1. Jos sitten tai.

Täältä saamme, ja.

2. Jos sitten tai.

Siitä lähtien.

Vastaus :,,,,

Esimerkki 8. Ratkaise yhtälö . (5)

Päätös. Niin kuin. Täältä ja yhtälöstä (5) Tästä seuraa, että eli eli Tässä on yhtälöjärjestelmä

Tämä yhtälöjärjestelmä on kuitenkin puutteellinen.

Vastaus: Ei juuria.

Esimerkki 9. Ratkaise yhtälö. (6)

Päätös.Jos nimeät, sitten ja yhtälöstä (6)

Tai. (7)

Koska yhtälö (7) on lomake, tämä yhtälö vastaa eriarvoisuutta. Täältä saamme. Siitä lähtien sitten tai.

Vastaus:.

Esimerkki 10. Ratkaise yhtälö. (8)

Päätös. Theoremin 1 mukaan voit tallentaa

(9)

Kun otetaan huomioon yhtälö (8), päätämme, että sekä epätasa-arvo (9) käsitellään tasa-arvossa, toisin sanoen toisin sanoen. Yhtälöiden järjestelmä on

Lause 3: n mukaan yllä oleva järjestelmä on kuitenkin tasaantunut epätasa-arvojärjestelmä

(10)

Eriarvoisuusjärjestelmän ratkaiseminen (10) Me saamme. Koska epätasa-arvojärjestelmä (10) vastaa yhtälöä (8), alkuperäisessä yhtälöllä on yksi juurta.

Vastaus:.

Esimerkki 11. Ratkaise yhtälö. (11)

Päätös. Albe, sitten tasa-arvovirrat yhtälöstä (11).

Täältä seuraa, että. Siten tässä on epätasa-arvojärjestelmä

Tämän epätasa-arvojärjestelmän ratkaisu on ja.

Vastaus :,.

Esimerkki 12. Ratkaise yhtälö. (12)

Päätös. Yhtälö (12) ratkaisee moduulien johdonmukaisen esityksen. Tehdä tämä, harkitse useita tapauksia.

1. Jos sitten.

1.1. Jos sitten.

1.2. Jos sitten. Mutta , Siksi tässä tapauksessa yhtälöllä (12) ei ole juuria.

2. Jos sitten.

2.1. Jos sitten.

2.2. Jos sitten.

Vastaus :,,,,,,

Esimerkki 13. Ratkaise yhtälö. (13)

Päätös. Koska yhtälön (13) vasen osa ei ole kaltainen, sitten. Tältä osin yhtälö (13)

vie näkymä tai.

Tiedetään, että yhtälö vastaa kahden yhtälön kokonaisuutta ja Ratkaisu, jonka saamme. Kuten , Että yhtälöllä (13) on yksi juurta.

Vastaus:.

Esimerkki 14. Ratkaise yhtälöjärjestelmän (14)

Päätös. Koska molemmat sitten. Näin ollen yhtälöjärjestelmästä (14) saamme neljä yhtälöjärjestelmää:

Edellä mainittujen yhtälöiden järjestelmien juuret ovat yhtälöiden järjestelmän juuret (14).

Vastaus :,,,,,,,

Esimerkki 15. Ratkaise yhtälöjärjestelmän (15)

Päätös. Siitä lähtien. Tältä osin yhtälöjärjestelmästä (15) saamme kaksi yhtälöjärjestelmää

Ensimmäisen yhtälön järjestelmän juuret ovat ja ja toisesta yhtälöistä, joita saamme ja.

Vastaus :,,,,

Esimerkki 16. Ratkaise yhtälöjärjestelmän (16)

Päätös. Järjestelmän ensimmäisestä yhtälöstä (16) Tästä seuraa.

Siitä lähtien . Harkitse järjestelmän toista yhtälöä. Sikäli kuinsitten ja yhtälö vie, tai.

Jos korvasi arvon Ensimmäisessä järjestelmän yhtälössä (16)Sitten, tai.

Vastaus :,.

Ongelmanratkaisumenetelmien syvemmälle tutkimukselle, liittyvät yhtälöiden ratkaisemiseen, sisältää muuttujia moduulin merkin alla, Voit neuvoa oppikirjoja suositellun kirjallisuuden luettelosta.

1. Matematiikan ongelmien kokoaminen maaperässä / ed. MI. Schanavi. - M.: Rauha ja koulutus, 2013. - 608 s.

2. Suprun V.P. Matematiikka lukion opiskelijoille: lisääntyneen monimutkaisuuden tehtävät. - M.: CD "libl" / urss, 2017. - 200 s.

3. Supran V.P. Matematiikka lukiolaisille: epätyypilliset menetelmät ongelmien ratkaisemiseksi. - M.: CD "libl" / urss, 2017. - 296 s.

Onko sinulla kysymyksiä?

Saadaksesi ohjaajan help - Rekisteröidy.

sivusto, jolla on täysi tai osittainen kopiointi materiaalin viittauksen alkuperäiseen lähteeseen.

Yhtälöiden ja epätasa-arvon ratkaiseminen moduulilla Usein aiheuttaa vaikeuksia. Kuitenkin, jos ymmärrät hyvin mitä numeron absoluuttinen arvo, I. miten paljastaa muutokset, jotka sisältävät moduulimerkinSitten läsnäolo yhtälössä ilmaisut moduulin merkki, lakkaa olemasta este sen ratkaisemiseksi.

Vähän teoriaa. Jokaisella numerolla on kaksi ominaisuutta: numeron absoluuttinen arvo ja sen merkki.

Esimerkiksi numero +5 tai yksinkertaisesti 5 on "+" -merkki ja absoluuttinen arvo 5.

Numero -5 on "-" merkki ja absoluuttinen arvo 5.

Numeron 5 ja -5 absoluutiset arvot ovat 5.

Numero X: n absoluuttinen arvo kutsutaan numeromoduuliksi ja merkitsee | x |.

Kuten näemme, numeron moduuli on yhtä suuri kuin numero, jos se on useita tai yhtä suuri kuin nolla, ja tämä numero vastakkaisella merkillä, jos se on negatiivinen numero.

Sama pätee kaikkiin lausekkeisiin, jotka seisovat moduulin merkin alla.

Moduulin julkistamissääntö näyttää tältä:

| f (x) | \u003d f (x), jos f (x) ≥ 0 ja

| f (x) | \u003d - f (x) jos f (x)< 0

Esimerkiksi X-3 | \u003d X-3, jos X-3≥0 ja | X-3 | \u003d - (X-3) \u003d 3-X, IF X-3<0.

Ratkaista yhtälön, joka sisältää ekspressiota, joka on moduulin merkkiä, on ensin kuvausmoduuli moduulin julkistamissäännön mukaan.

Sitten yhtälö tai epätasa-arvo muutetaan kahdessa eri yhtälössä, jotka ovat kahdessa eri numeerisella välein.

Yksi yhtälö on olemassa numeerisessa aukossa, jossa ekspressio, joka seisoo moduulin merkin alla, ei ole emallistamatonta.

Ja toinen yhtälö on aikavälillä, jossa ilmaisu, joka seisoo moduulin merkkiä, on negatiivinen.

Harkitse yksinkertainen esimerkki.

Ryhmäten ratkaiseminen:

| X-3 | \u003d -X 2 + 4X-3

1. Irrota moduuli.

| X-3 | \u003d X-3, IF X-3≥0, ts. Jos x≥3.

| X-3 | \u003d - (X-3) \u003d 3-X, IF X-3<0, т.е. если х<3

2. Saimme kaksi numeerista aukkoa: x≥3 ja x<3.

Harkitse, miten yhtälöt muunnetaan alkuperäiseen yhtälöön kussakin välein:

A) x≥3 | x-3 | \u003d x-3, ja sulkemme ovat:

Huomio! Tämä yhtälö on vain intervallisella x≥3!

Me paljastamme suluja, annamme tällaisia \u200b\u200bjäseniä:

ja ratkaista tämä yhtälö.

Tämä yhtälö on juuri:

x 1 \u003d 0, x 2 \u003d 3

Huomio! Koska yhtälö X-3 \u003d -X 2 + 4x-3 on vain GAP X≥3, olemme kiinnostuneita vain tähän aukon juurista. Tämä tila täyttää vain x 2 \u003d 3.

B) X: n kanssa<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Huomio! Tämä yhtälö on vain välein<3!

Avaa suluja, annamme tällaisia \u200b\u200bjäseniä. Saamme yhtälön:

x 1 \u003d 2, x 2 \u003d 3

Huomio! Koska 3-X \u003d -x 2 + 4x-3 -yhtävyys on olemassa vain Interval x: ssä<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Joten: Ensimmäisestä aukosta otetaan vain juuri x \u003d 3, toisesta - juuresta x \u003d 2.

Joukossa esimerkkejä moduuleista Usein on yhtälöitä, joissa sinun täytyy löytää root-moduuli moduulissaeli lomakkeen yhtälö
|| A * X-B | -C | \u003d k * x + m.
Jos K \u003d 0, toisin sanoen oikea puoli on yhtä suuri kuin vakio (M), on helpompi etsiä liuosta yhtälöt, joissa moduulit graafisesti. Alla on tekniikka kaksoismoduulien tiedot Yhteisissä esimerkeissä käytännössä. Noudata algoritmia yhtälöiden laskemiseksi moduuleilla, jotta ei ole ongelmia hallita, testejä ja vain tietää.

Esimerkki 1. Ratkaise yhtälömoduuli moduulissa 3 | x | -5 | \u003d -2x-2.
Ratkaisu: alkaa aina paljastaa yhtälöt sisäisestä moduulista
| x | \u003d 0 <-> X \u003d 0.
Kohdassa X \u003d 0 moduulin yhtälöt jaetaan 2: een.
X: n kanssa.< 0 подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
| -3x-5 | \u003d -2x-2.
X\u003e 0 tai yhtä suuri, paljastaen moduulin
| 3x-5 | \u003d -2x-2.
Yhtälön ratkaiseminen negatiivisille muuttujille (x< 0) . Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе - раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная - меняем знак правой или левой части (зависит от методики преподавания).

Ensimmäisestä yhtälöstä saamme, että ratkaisu ei saa ylittää (-1), ts.

Tämä rajoitus kuuluu täysin alueelle, jossa päätämme. Siirrämme muuttujia ja pysyviä tasa-arvon eri puolille ensimmäisessä ja toisessa järjestelmässä

ja löytää ratkaisu


Molemmat arvot kuuluvat aukkoon, jota pidetään, eli ne ovat juuret.
Harkitse yhtälöä moduuleilla positiivisilla muuttujilla
| 3x-5 | \u003d -2x-2.
Moduulin paljastaminen Saavutamme kaksi yhtälöjärjestelmää

Ensimmäisestä yhtälöstä, joka on yhteinen kahdelle Sissumille, saamme tutun tilan

Joka risteyksessä, jossa on joukko, josta etsimme ratkaisua, antaa tyhjän sarjan (ei risteyspisteitä). Joten moduulin ainoa juuret moduulilla ovat arvoja
x \u003d -3; x \u003d -1.4.

Esimerkki 2. Ratkaise yhtälö moduulilla || X-1 | -2 | \u003d 3x-4.
Ratkaisu: Aloita sisäisen moduulin julkistamisesta
| x-1 | \u003d 0 <=> x \u003d 1.
Avioluettelon toiminto muuttaa merkkiä yhteen. Alemmilla arvoilla on negatiivinen, suurella positiivisella. Tämän mukaisesti, kun sisäisen moduulin paljastaminen saat kaksi yhtälöä moduulilla
x | - (X - 1) -2 | \u003d 3X-4;
X\u003e \u003d 1 -\u003e | X-1-2 | \u003d 3X-4.
Varmista, että yhtälön oikea puoli moduulilla on nolla.
3x-4\u003e \u003d 0 -\u003e X\u003e \u003d 4/3.
Tämä tarkoittaa, että ensimmäinen yhtälöstä ei ole tarpeen päättää, se on riippuvainen X: stä< 1, что не соответствует найденному условию. Раскроем модуль во втором уравнении
| X-3 | \u003d 3X-4 ->
X-3 \u003d 3X-4 tai x-3 \u003d 4-3x;
4-3 \u003d 3x-x tai x + 3x \u003d 4 + 3;
2x \u003d 1 tai 4x \u003d 7;
x \u003d 1/2 tai x \u003d 7/4.
Vastaanotettu kaksi arvoa, joista ensimmäinen hylkäämme, koska se ei kuulu haluttuun aikaväliin. Lopuksi yhtälöllä on yksi ratkaisu X \u003d 7/4.

Esimerkki 3. Ratkaise yhtälö moduulilla || 2x-5 | -1 | \u003d x + 3.
Ratkaisu: Poista sisäinen moduuli
| 2x-5 | \u003d 0 <=> x \u003d 5/2 \u003d 2.5.
Piste X \u003d 2,5 jakautuu numeerisen akselin kahteen väliltaan. Vastaavasti, abladeule-toiminto Muuttaa merkkiä, kun siirryt 2.5 jälkeen. Jäämme olestimme yhtälön oikealla puolella olevasta ratkaisusta moduulin kanssa.
X + 3\u003e \u003d 0 -\u003e x\u003e \u003d - 3.
Joten ratkaisu voi olla arvoja, jotka ovat vähintään (-3). Paljastamme moduulin sisäisen moduulin negatiiviselle arvolle
| - (2x-5) -1 | \u003d x + 3;
| -2x + 4 | \u003d x + 3.
Tämä moduuli antaa myös 2 yhtälöä, kun paljastetaan
-2x + 4 \u003d x + 3 tai 2x-4 \u003d x + 3;
2x + x \u003d 4-3 tai 2x-x \u003d 3 + 4;
3x \u003d 1; x \u003d 1/3 tai x \u003d 7.
Arvo X \u003d 7 Hylkää, kun etsimme liuosta Interval [-3; 2.5]. Nyt paljastaa x\u003e 2.5: n sisäinen moduuli. Saavutamme yhtälön yhdellä moduulilla
| 2x-5-1 | \u003d x + 3;
| 2x-6 | \u003d x + 3.
Kun moduulin paljastaminen saat seuraavat lineaariset yhtälöt
-2x + 6 \u003d x + 3 tai 2x-6 \u003d x + 3;
2x + x \u003d 6-3 tai 2x-x \u003d 3 + 6;
3x \u003d 3; x \u003d 1 tai x \u003d 9.
Ensimmäinen arvo X \u003d 1 ei täytä X\u003e 2.5-tilaa. Joten tällä hetkellä meillä on yksi juuret yhtälöstä moduulilla x \u003d 9, ja kaikki ne ovat kaksi (x \u003d 1/3). Tyylikäs voidaan tarkistaa oikein laskenta
Vastaus: X \u003d 1/3; x \u003d 9.

Esimerkki 4. Etsi kaksoismoduulin ratkaisut || 3x-1 | -5 | \u003d 2x-3.
Ratkaisu: Poista sisäinen yhtälömoduuli
| 3x-1 | \u003d 0 <=> X \u003d 1/3.
Piste X \u003d 2.5 jakaa numeerisen akselin kahdella välein ja tietyn yhtälön kaksi tapausta. Kirjoita liuoksen ehto, joka perustuu yhtälön näkymään oikealla puolella
2x-3\u003e \u003d 0 -\u003e x\u003e \u003d 3/2 \u003d 1,5.
Tästä seuraa, että olemme kiinnostuneita arvoista\u003e \u003d 1.5. Tällä tavalla modulaarinen yhtälö Pidämme kaksi välein
,
| - (3x-1) -5 | \u003d 2x-3;
| -3x-4 | \u003d 2x-3.
Tuloksena oleva moduuli paljastuksen aikana on jaettu 2 yhtälöön
-3x-4 \u003d 2x-3 tai 3x + 4 \u003d 2x-3;
2x + 3x \u003d -4 + 3 tai 3x-2x \u003d -3-4;
5x \u003d -1; X \u003d -1 / 5 tai x \u003d -7.
Molemmat arvot eivät kuulu aukkoon, eli ei ole yhtälöitä, joissa on moduulit. Seuraavaksi paljasta X\u003e 2.5-moduuli. Saavutamme seuraavan yhtälön
| 3x-1-5 | \u003d 2x-3;
| 3x-6 | \u003d 2x-3.
Moduulin paljastaminen, saamme 2 lineaarista yhtälöä
3x-6 \u003d 2x-3 tai - (3x-6) \u003d 2x-3;
3x-2x \u003d -3 + 6 tai 2x + 3x \u003d 6 + 3;
x \u003d 3 tai 5x \u003d 9; X \u003d 9/5 \u003d 1.8.
Toinen arvo säätiöstä ei vastaa tilannetta x\u003e 2.5, hylkäämme sen.
Lopuksi meillä on yksi yhtälön juuret moduuleilla x \u003d 3.
Suorittaa tarkistus
||3*3-1|-5|=2*3-3 3=3 .
Yhtäluonteen juuret moduulin kanssa lasketaan oikein.
Vastaus: X \u003d 1/3; x \u003d 9.

Tämä matemaattinen laskin auttaa sinua ratkaise yhtälö tai epätasa-arvo moduuleilla. Ohjelma yhtälöiden ja epätasa-arvot moduuleilla ei vain anna vastaustehtävälle, se johtaa yksityiskohtainen päätös selitysten kanssa. Näyttää tulosprosessin.

Tämä ohjelma voi olla hyödyllinen yleiskoulujen korkeakoulujen opiskelijoille, kun valmistaudut testeihin ja tentteihin, kun tarkastetaan tietoa ennen tenttiä, vanhemmat valvonta monien matematiikan ja algebran ongelmien ratkaisemiseksi. Tai ehkä olet liian kallista palkata opettaja tai ostaa uusia oppikirjoja? Tai haluat vain tehdä kotitehtäväsi matematiikassa tai algebra mahdollisimman? Tässä tapauksessa voit myös käyttää ohjelmiamme yksityiskohtaisella ratkaisulla.

Näin voit tehdä oman koulutuksen ja nuorempien veljen tai sisarien koulutusta, kun taas koulutuksen taso ratkaistavien tehtävien alalla kasvaa.

| X | tai ABS (X) - Moduuli X

Syötä yhtälö tai epätasa-arvo moduuleilla

Ratkaise yhtälö tai epätasa-arvo

Todettiin, että joitain tämän tehtävän ratkaisemiseen tarvittavat komentosarjat eivät ole ladattuja, ja ohjelma ei välttämättä toimi.
Sinulla voi olla Adblock mukana.
Tässä tapauksessa irrota se ja päivitä sivu.

Sinulla on JavaScript-toteutus selaimessasi.
Jos haluat tehdä ratkaisun, sinun on otettava JavaScript käyttöön.
Seuraavassa on ohjeet, miten JavaScript ottaa käyttöön selaimessasi.

Koska Haluatko ratkaista tehtävä on hyvin paljon, pyyntösi on linjassa.
Muutaman sekunnin kuluttua liuos tulee näkyviin alla.
Odota Sec ...

Jos sinä huomasi virheen ratkaisemisessaVoit kirjoittaa siitä palautelomakkeessa.
Älä unohda määritä mikä tehtävä Päätät ja mitä anna kentälle.

Pelit, palapelit, emulaattorit:

Vähän teoriaa.

Yhtälöt ja epätasa-arvo moduuleilla

Pääkoulun algebrien kulku voi täyttää yksinkertaisimmat yhtälöt ja eriarvoisuudet moduuleilla. Niiden ratkaisemiseksi on mahdollista soveltaa geometrista menetelmää, joka perustuu siihen, että \\ (| xa | \\) on etäisyys numeerisesta pisteestä X ja A: \\ (| XA | \u003d \\ RHO (x; \\ ; a) \\). Esimerkiksi yhtälön (| x-3 | \u003d 2 \\) ratkaisemiseksi on välttämätöntä löytää numeerinen suora kohta, poistettu 3 pisteestä etäisyydelle 2. Tällaisia \u200b\u200bseikkoja on kaksi (x_1 \u003d 1 \\) ja \\ (x_2 \u003d 5 \\).

Epätasa-arvojen ratkaiseminen \\ (| 2x + 7 |

Mutta tärkein tapa ratkaista yhtälöitä ja epätasa-arvoa moduuleilla, liittyy niin sanottuun "moduulin paljastamiseen määritelmän mukaan":
Jos \\ (a \\ geq 0 \\), sitten \\ (| a | \u003d a \\);
Jos esimerkiksi yhtälö (epätasa-arvo) moduuleilla vähennetään yhtälöiden kokonaismäärään (eriarvoisuuksia), jotka eivät sisällä moduulimerkkiä.

Määritetyn määritelmän lisäksi käytetään seuraavia väitteitä:
1) jos \\ (c\u003e 0 \\), niin yhtälö \\ (| f (x) | \u003d c \\) vastaa yhtälöitä: \\ (vasen [aloitus (array) (l) f (x ) \u003d C \\\\ f (x) \u003d - c \\ end (array) oikea. \\)
2) Jos \\ (c\u003e 0 \\), sitten epätasa-arvoinen \\ (| f (x) 3) Jos \\ (C \\ GEQ 0 \\), sitten epätasa-arvo \\ (f (x)\u003e c \\) vastaa Täydellinen epätasa-arvo: \\ (vasen [aloitus (array) (l) f (x) c \\ end (array) oikean. \\)
4) Jos molemmat osat epätasa-arvosta \\ (f (x) Esimerkki 1. Ratkaise yhtälö \\ (x ^ 2 +2 | X-1 | -6 \u003d 0 \\).

Jos \\ (x-1 \\ geq 0 \\), sitten \\ (| x-1 | \u003d x-1 \\) ja määritetty yhtälö ottaa lomakkeen
\\ (x ^ 2 +2 (x - 1) -6 \u003d 0 \\ Oikea X ^ 2 + 2x -8 \u003d 0 \\).
Jos \\ (x-1 \\ (x ^ 2 -2 (x - 1) -6 \u003d 0 \\ närakko x ^ 2 -2x -4 \u003d 0 \\).
Siten määritettyä yhtälöä olisi harkittava erikseen kussakin näistä kahdesta tapauksesta.
1) Olkoon \\ (x - 1 \\ geq 0 \\), ts. \\ (X \\ GEQ 1 \\). Yhtälöstä \\ (x ^ 2 + 2x -8 \u003d 0 \\) löydämme \\ (x_1 \u003d 2, \\; x_2 \u003d -4 \\). Ehto \\ (X \\ GEQ 1 \\) täyttää vain arvo \\ (x_1 \u003d 2 \\).
2) Olkoon \\ (x-1 vastaus: \\ (2; \\; 1- \\ sqrt (5) \\)

Esimerkki 2. Ratkaise yhtälö \\ (| x ^ 2-6x + 7 | \u003d \\ frac (5x-9) (3) \\).

Ensimmäinen menetelmä (Moduulin paljastaminen määritelmän mukaan).
Kuten esimerkiksi esimerkissä 1, päätämme, että määritettyä yhtälöä olisi harkittava erikseen kahden ehdon suorittamisen aikana: \\ (x ^ 2-6x + 7 \\ (x ^ 2-6x + 7

1) jos \\ (x ^ 2-6x + 7 \\ geq 0 \\), sitten \\ (| x ^ 2-6x + 7 | \u003d x ^ 2-6x + 7 \\) ja määritetty yhtälö ottaa lomakkeen \\ (x ^ 2 -6x + 7 \u003d \\ frac (5x-9) (3) \\ Kaapii 3x ^ 2-23x + 30 \u003d 0 \\). Päättää tämä neliöyhtälö, saamme: \\ (x_1 \u003d 6, \\; x_2 \u003d \\ frac (5) (3) \\).
Selvitämme, täyttääkö arvo \\ (x_1 \u003d 6 \\) edellytyksen \\ (x ^ 2-6x + 7 \\ geq 0 \\). Tätä varten korvaamme määritetyn arvon neliön epätasa-arvoon. Saamme: \\ (6 ^ 2-6 \\ CDOT 6 + 7 \\ GEQ 0 \\), ts. \\ (7 \\ GEQ 0 \\) - Uskollinen epätasa-arvo. Joten, \\ (x_1 \u003d 6 \\) on tietyn yhtälön juuret.
Selvitämme, täyttääkö arvo \\ (x_2 \u003d \\ frac (5) (3) \\) edellytys \\ (x ^ 2-6x + 7 \\ geq 0 \\). Tätä varten korvaamme määritetyn arvon neliön epätasa-arvoon. Saamme: \\ (vasemmalle (\\ frac (5) (3) oikealla) ^ 2 - frac (5) (3) \\ CDOT 6 + 7 \\ GEQ 0 \\), ts. \\ (\\ FRAC (25) (9) -3 \\ GEQ 0 \\) - Väärä epätasa-arvo. Joten, \\ (x_2 \u003d \\ frac (5) (3) \\) ei ole tietyn yhtälön juuret.

2) jos \\ (x ^ 2-6x + 7, arvo \\ (x_3 \u003d 3 \\) täyttää kunnon \\ (x ^ 2-6x + 7, arvo \\ (x_4 \u003d \\ frac (4) (3) \\ t ) Ei täytä ehtoa \\ (x ^ 2-6x + 7, määritetyssä yhtälöllä on kaksi juuria: \\ (x \u003d 6, \\; x \u003d 3 \\).

Toisella tavalla. Jos yhtälö on annettu \\ (| f (x) | \u003d h (x) \\), sitten \\ (h (x) \\ (vasen [aloitus (array) (l) x ^ 2-6x + 7 \u003d \\ Frac (5x-9) (3) \\\\ X ^ 2-6x + 7 \u003d - \\ frac (5x-9) (3) \\ Pääty (array) oikealla. \\)
Molemmat näistä yhtälöistä ratkaistaan \u200b\u200bedellä (ensimmäinen menetelmä tietyn yhtälön ratkaisemiseksi), niiden juuret ovat seuraavat: \\ (6, \\; \\ frac (5) (3), \\; 3, \\; \\ frac (4 ) (3) \\). Näistä neljästä arvosta vastaava tilanne \\ (\\ frac (5x-9) (3) \\ t X \u003d 3 \\).

Kolmas tapa (graafinen).
1) Rakentamme funktiotaikataulun \\ (y \u003d | x ^ 2-6x + 7 | \\). Ensinnäkin me rakentaa parabolaa \\ (y \u003d x ^ 2-6x + 7 \\). Meillä on \\ (x ^ 2-6x + 7 \u003d (x-3) ^ 2-2 \\). Toiminnon (y \u003d (x-3) ^ 2-2 \\) kaavio voidaan saada funktion funktiosta \\ (Y \u003d X ^ 2 \\) siirrä se 3 yksikköä asteikolla oikealle ( X-akselilla) ja 2 yksikköä alaspäin (Y-akselilla). Direct X \u003d 3 - Parabolasin akseli olet kiinnostunut. On kätevää ottaa piste (3; -2) - Vertex parabola, kohta (0; 7) ja symmetrinen parabolalla (6; 7).
Toiminnan aikataulun rakentaminen \\ (y \u003d | x ^ 2-6x + 7 | \\) on poistuttava muuttamatta polerabolin osaa, joka ei ole X-akselin alapuolella ja parabolan osa Se sijaitsee X-akselin alapuolella, jolloin voit näyttää X-akselin peilin.
2) Rakentamme graafin lineaarisesta toiminnasta \\ (Y \u003d \\ FRAC (5X-9) (3). Testipisteinä on kätevää ottaa pisteitä (0; -3) ja (3; 2).

On huomattavaa, että piste X \u003d 1.8 Suoran akselin risteyksessä sijaitsee oikein parabolan ylijäämän vasemmanpuoleisen risteyksestä abscissan akselilla on piste \\ (x \u003d 3- \\ sqrt ( 2) \\ t (3- \\ sqrt (2) 3) Piirustuksen perusteella kaaviot leikkaavat kahdessa kohdassa - A (3, 2) ja (6; 7). Näiden pisteiden settimet X X \u003d 3 ja x \u003d 6 tietylle yhtälöön olemme vakuuttuneita siitä, että vaikka toinen merkitys on oikea numeerinen tasa-arvo. Joten meidän hypoteesi vahvistettiin - yhtälöllä on kaksi juuria: X \u003d 3 ja X \u003d 6. Vastaa: 3; 6 .

Kommentti. Graafinen menetelmä kaikkiin armonsa kanssa ei ole kovin luotettava. Tutkittussa esimerkissä se toimi vain siksi, että yhtälön juuret ovat kokonaislukuja.

Esimerkki 3. Ratkaise yhtälö \\ (| 2x-4 | + | x + 3 | \u003d 8 \\)

Ensimmäinen menetelmä
Ilmennys 2x-4 viittaa 0 pisteeseen X \u003d 2 ja ekspressio X + 3 on pisteessä X \u003d -3. Nämä kaksi pistettä rikkovat numeerista suoraan kolmeen aukkoon: \\ (x

Harkitse ensimmäinen aikaväli: \\ (- - \\ infty; -3) \\).
Jos X harkitse toista aukkoa: \\ ([- 3; \\; 2) \\).
Jos \\ (- 3 \\ Leq X harkitsee kolmannen aukon: \\ ( Vastaus: GAP: n pituus on 6.№3 . Päätä yhtälö, vastauksena määrittää ratkaisut: │2 + X - x 2 │ \u003d 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Vastaus: 4 ratkaisua.№4 . Päätä yhtälö, vastaa suurimmasta juuri:
│4 - x -
│ \u003d 4 - x -
X 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Vastaus: X \u003d 3.

Harjoitukset: №12. Päätä yhtälö, vastaa vastauksesta, määritä koko juuret: │x 2 + 6x + 8│ \u003d x 2 + 6x + 8 №13. Ratkaise yhtälö, vastaa vastauksena koko ratkaisujen lukumäärä: │13x - x 2 - 366 + x 2 - 13x + 36 \u003d 0 №14. Päätä yhtälö, vastauksena määrittää kokonaisluku, joka ei ole yhtälön juuret:

Osa 5. Lomakkeen yhtälöt │F (x) │ \u003d │g (x) │

Koska yhtälön molemmat osat eivät ole negatiivisia, niin ratkaisu merkitsee kahden tapauksen huomioon ottamista: Abladuli-ilmaisut ovat yhtä tai vastakkaisia \u200b\u200bmerkkiä. Näin ollen alkuperäinen yhtälö vastaa kahden yhtälön kokonaisuutta: │ F.(x.)│= │ G.(x.)│
Esimerkkejä: №1. Päätä yhtälö, vastauksessa määritä koko juuret: │x + 3│ \u003d │2x - 1│
Vastaus: Koko juuret x \u003d 4.№2. Ratkaise yhtälö: │ x - X 2 - 1│ \u003d │2X - 3 - X 2 │
Vastaus: X \u003d 2.№3 . Päätä yhtälö, vastauksessa määritä juurien tuote:




CorValating 4x 2 + 2x - 1 \u003d 0 x 1.2 \u003d - 1 ± √5 / 4 Vastaus: Juurien tuote on 0,25. Harjoitukset: №15 . Päätä yhtälö, vastaakaa, määritä koko ratkaisu: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Ratkaise yhtälö, vastauksena, määritä pienempi root: │5x - 3│ \u003d │7 - x│ №17 . Ratkaise yhtälö vastauksesta, määritä juurien määrä:

KOHTA 6. Esimerkkejä epätyypillisten yhtälöiden ratkaisemisesta

Tässä osiossa tarkastelemme esimerkkejä epätyypillisistä yhtälöistä, kun ratkaistaan, mikä ilmaisun absoluuttinen arvo kuvataan määritelmän mukaan. Esimerkkejä:

№1. Ratkaise yhtälö vastauksessasi, määritä juurien määrä: X · │ │-5x - 6 \u003d 0
Vastaus: Juurien määrä on 1 №2. . Ratkaise yhtälö, vastauksena, määritä pienempi root: X 2 - 4x ·
- 5 = 0
Vastaus: Little Root X \u003d - 5. №3. Ratkaise yhtälö:

Vastaus: X \u003d -1. Harjoitukset: №18. Päätä yhtälö ja määritä juurien määrä: X · │3x + 5│ \u003d 3x 2 + 4x + 3
№19. Ratkaise yhtälö: x 2 - 3x \u003d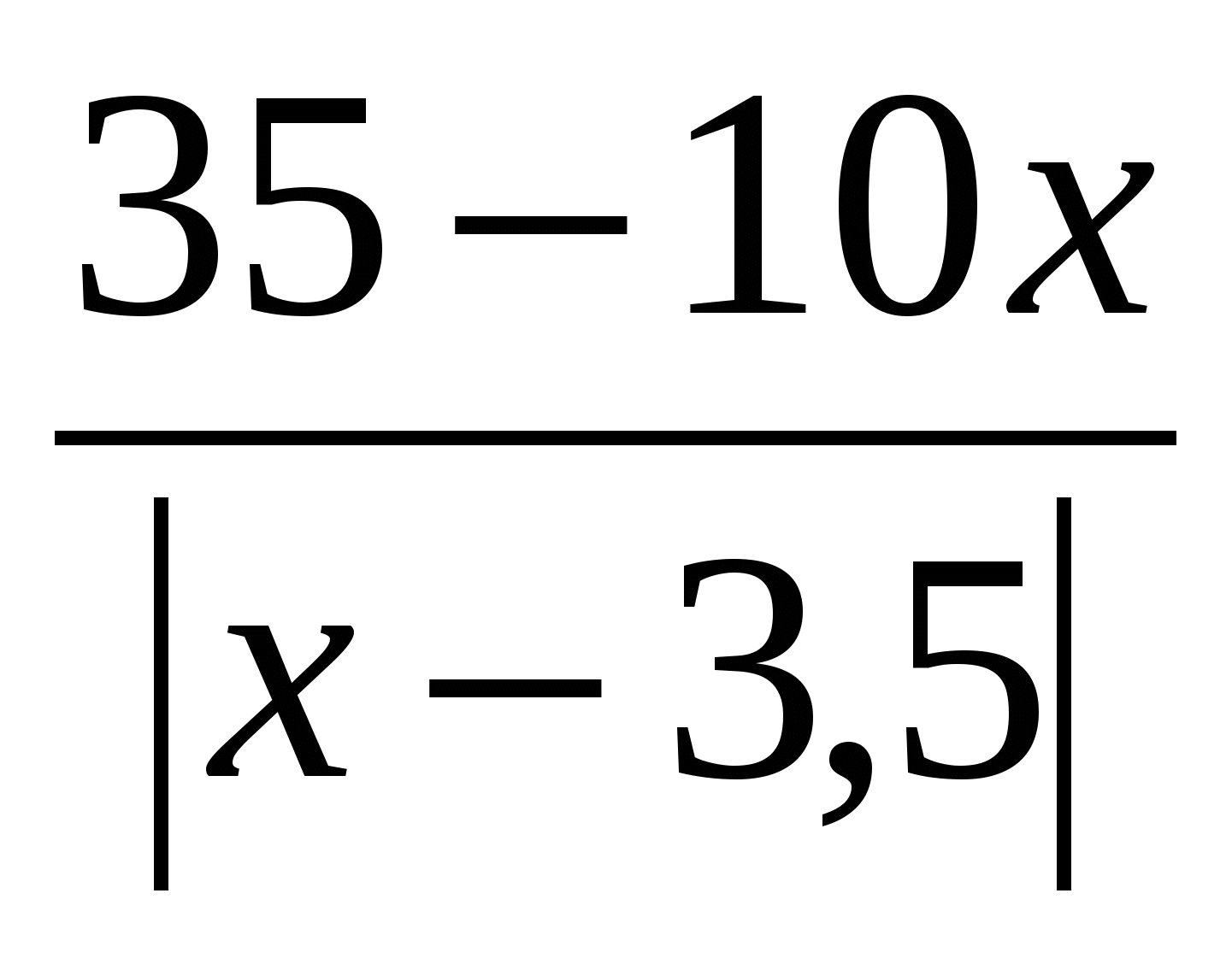

№20. Ratkaise yhtälö:

Osa 7. Lomakkeen yhtälöt │F (x) │ + │g (x) │ \u003d 0

On helppo nähdä, että tämäntyyppisten ei-negatiivisten arvojen yhtälön vasemmalla puolella. Näin ollen alkuperäisessä yhtälöllä on ratkaisu, jos ja vain, jos molemmat komponentit ovat samanaikaisesti yhtä suuret kuin nolla. Yhtälö vastaa yhtälöjärjestelmää: │ F.(x.)│+│ G.(x.)│=0
Esimerkkejä: №1 . Ratkaise yhtälö:
Vastaus: X \u003d 2. №2. Ratkaise yhtälö: Vastaus: X \u003d 1. Harjoitukset: №21. Ratkaise yhtälö: №22 . Ratkaise yhtälö vastauksesta, määritä juurien määrä: №23 . Päättää yhtälöstä vastauksena määrittää ratkaisujen määrä:

Osa 8. Lomakkeen yhtälöt │A 1 x + 1 │ ± │ 2 x + 2 ± ... │A n x + n │ \u003d m

Tämän lajin yhtälöiden ratkaisemiseksi käytetään väliaikaa. Jos ratket moduulien johdonmukaisen julkistamisen, saamme n. Järjestelmien soittoisuudet, jotka ovat erittäin hankalia ja epämukavia. Harkitse aikavälin menetelmän algoritmia: 1). Etsi muuttujan arvot h. jossa jokainen moduuli on nolla (alemoduulin ilmaisujen nollia):
2). Löydettyjä arvoja, jotka löytyvät numeerisesta suorasta, joka hajoaa välein (vastaavasti väliajoin) n.+1 ) 3). Jokaisen moduulin paljastaminen jokaisella moduulilla on paljastanut jokaisen moduulin (kun dekompomrialia, voit käyttää numeerista suoria, merkintämerkkejä siihen) 4). Alkuperäinen yhtälö vastaa kokonaisuutta n.+1 Järjestelmät, joista kukin osoittaa muuttujan henkilöllisyyden h. Yksi välein. Esimerkkejä: №1 . Päätä yhtälö, vastaa suurimmasta juuri:
yksi). Löydämme alemoduulin ilmaisujen nollia: x \u003d 2; x \u003d -3 2). Huomaa havaitut arvot numeerisessa suorassa ja määrittävät, miten kukin moduuli paljastuu tuloksena olevaan välein:
X - 2 x - 2 x - 2 - - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- Ei ratkaisuja Yhtälöllä on kaksi juuria. Vastaus: Suurin juuret x \u003d 2. №2. Ratkaise yhtälö vastauksena, määritä koko juuret:
yksi). Löydämme alemoduulin ilmaisujen nollia: x \u003d 1,5; X \u003d - 1 2). Huomaa havaitut arvot numeerisen suoran ja määrittämään, jonka avulla jokainen moduuli paljastuu tuloksena olevaan välein: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x - 3 2x - 3 2x - 3 - - +
3).
Jälkimmäisessä järjestelmässä ei ole ratkaisuja, joten yhtälöllä on kaksi juuria. Yhtälön ratkaisun aikana kiinnitä huomiota toiseen moduuliin. Vastaus: Koko juuret x \u003d 7. №3. Päätä yhtälö vastaus, määritä juurien määrä: 1). Löydämme sukelluslevyjen ekspressiot: x \u003d 5; x \u003d 1; X \u003d - 2 2). Huomaa numeerisen suoran löytämät arvot ja määritä, kuinka kukin moduuli paljastuu tuloksena olevaan välein: X - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x - 1 x - 1 x - 1 x - 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Yhtälöllä on kaksi juuria x \u003d 0 ja 2. Vastaus: Juurien määrä on 2. №4 . Päätä yhtälö: 1). Löydämme alemoduulin ilmaisujen nollia: x \u003d 1; x \u003d 2; x \u003d 3. 2). Määritämme, kuinka jokainen moduuli saadaan aikaan. 3).
Yhdistä ensimmäisten kolmen järjestelmän ratkaisut. Vastaus:; X \u003d 5.
Harjoitukset: №24. Ratkaise yhtälö:
№25. Ratkaise yhtälö vastauksesta, määritä juurien määrä: №26. Päätä yhtälö, vastauksena, määritä pienempi root: №27. Päätä yhtälö, vastauksena, määritä suurempi root:

KOHTA 9. Yhtälöt, jotka sisältävät useita moduuleja

Yhtälöt, jotka sisältävät useita moduuleja, ottavat absoluuttisten arvojen läsnäolon aliratuisissa ilmaisuissa. Tämän lajin yhtälöiden ratkaisemisen perusperiaate on johdonmukainen moduulien julkistaminen, joka alkaa "ulkoisesta". Ratkaisun aikana käytetään 1 osassa 1, nro 3 olevia tekniikoita.

Esimerkkejä: №1. Ratkaise yhtälö:
Vastaus: X \u003d 1; - yksitoista. №2. Ratkaise yhtälö:
Vastaus: X \u003d 0; neljä; - neljä. №3. Päätä yhtälö, vastauksessa määritä juurien tuote:
Vastaus: Juurien tuote on - 8. №4. Ratkaise yhtälö:
Merkitse aggregaatin yhtälö (1) ja (2) Ja harkitse kunkin niistä ratkaisua erikseen suunnittelun helpottamiseksi. Koska molemmat yhtälöt sisältävät useamman kuin yhden moduulin, on helpompaa suorittaa vastaava siirtyminen järjestelmien sarjoihin. (1)

(2)


Vastaus:
Harjoitukset: №36. Päätä yhtälö, vastauksena määrittää juurien määrä: 5 │3x-5│ \u003d 25 x №37. Päätä yhtälö, jos juuret yli yksi, vastauksessa määritä juurien määrä: │x + 2│ x - 3x - 10 \u003d 1 №38. Ratkaise yhtälö: 3 │2x -4│ \u003d 9 │ │ №39. Ratkaise yhtälö, vastauksena määritä juurien määrä: 2 │ SIN X│ \u003d √2 №40 . Ratkaise yhtälö, vastauksena määritä juurien määrä:

Osa 3. Logaritminen yhtälöt.

Ennen seuraavien yhtälöiden ratkaisemista on tarpeen toistaa logaritmien ja logaritmisen toiminnon ominaisuudet. Esimerkkejä: №1. Päätä yhtälö, vastaa juurien tuote: log 2 (x + 1) 2 + log 2 │x + 1│ \u003d 6 OD. x + 1 ≠ 0 x ≠ - 1

1 tapaus: jos x ≥ - 1, sitten log 2 (x + 1) 2 + log 2 (x + 1) \u003d 6 log 2 (x + 1) 3 \u003d log 2 2 6 (x + 1) 3 \u003d 2 6 x + 1 \u003d 4 x \u003d 3 - tyydyttää tilan x ≥ - 1 2 kotelo: Jos x log 2 (x + 1) 2 + loki 2 (-X-1) \u003d 6 log 2 (x + 1) 2 + loki 2 (- (x + 1)) \u003d 6 log 2 (- (x + 1) 3) \u003d log 2 2 6- (x + 1) 3 \u003d 2 6- (x + 1) \u003d 4 x \u003d - 5 - Täyttää ehto X - 1
Vastaus: Juurien tuote on - 15.
№2. Päättää yhtälöstä vastauksella, määritä juurien määrä: LG
Od

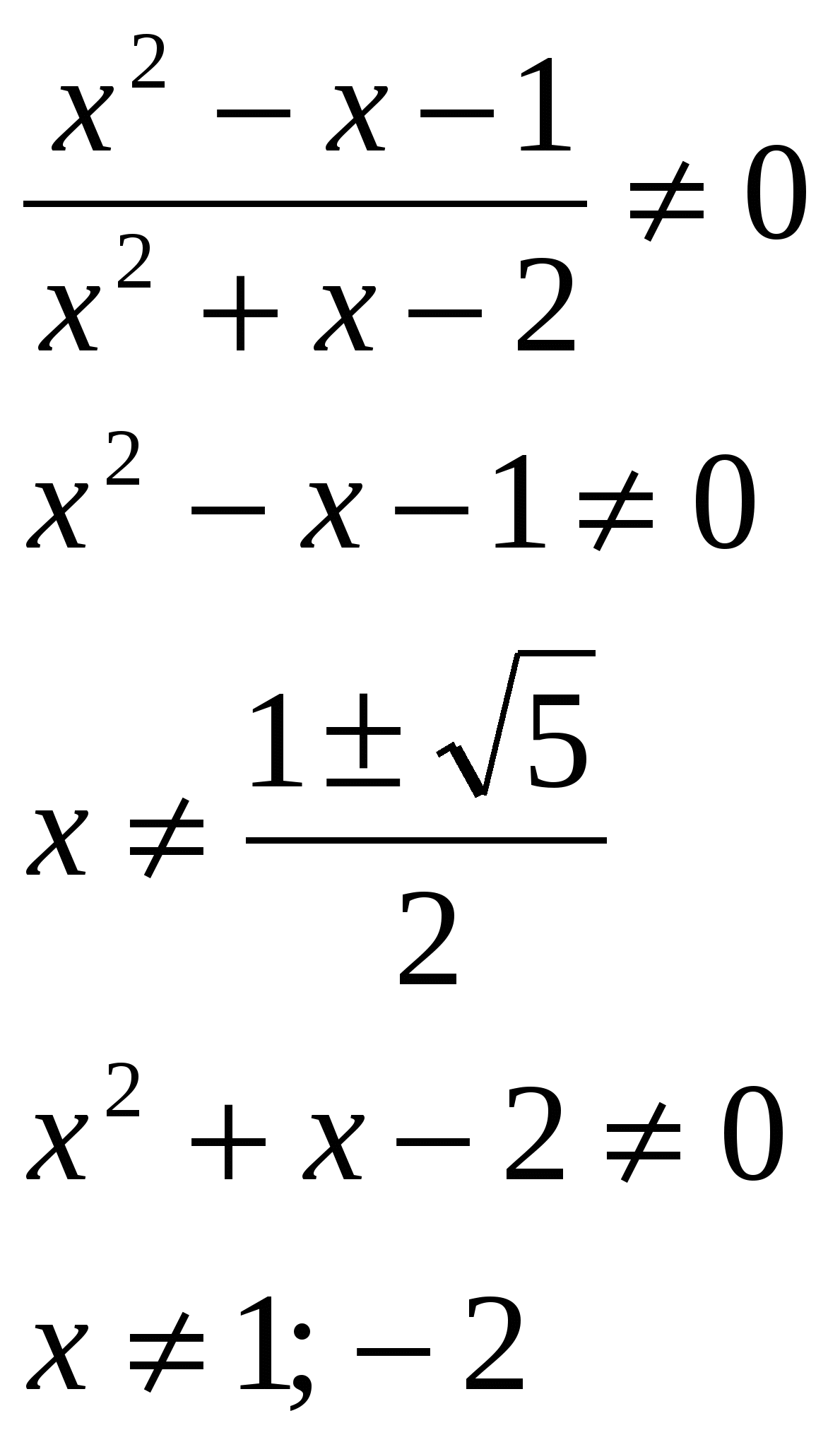
Vastaus: Juurien määrä on 0,5.
№3. Ratkaise yhtälö: log 5
Od

Vastaus: X \u003d 9. №4. Päätä yhtälö: │2 + log 0.2 x│ + 3 \u003d │1 + loki 5 x│ OD X\u003e 0 Käytämme siirtymistä toiseen pohjaan. │2 - LOG 5 x│ + 3 \u003d │1 + loki 5 x│
│2 - LOG 5 X│- │1 + LOG 5 x│ \u003d - 3 Löydämme sukelluslevyjen ekspressiot: x \u003d 25; X \u003d Nämä numerot jaetaan sallituilla arvoilla kolmella väleellä, joten yhtälö vastaa kolmea järjestelmää.
Vastaus :)