Hvordan beregne den inverse matrisen. Finn invers matrise på nettet. Ved hjelp av en kalkulator

Matrix Algebra - Invers Matrix

invers matrise

invers matrise En matrise kalles som, multiplisert både til høyre og til venstre med en gitt matrise, gir identitetsmatrisen.
Angi matrisen invers til matrisen MEN gjennom , så får vi i henhold til definisjonen:

hvor E er identitetsmatrisen.
kvadratisk matrise kalt ikke-spesiell (ikke-degenerert) hvis determinanten ikke er lik null. Ellers heter det spesiell (degenerert) eller entall.

Det er et teorem: hver ikke-singular matrise har en invers matrise.

Operasjonen med å finne den inverse matrisen kalles anke matriser. Tenk på matriseinversjonsalgoritmen. La en ikke-singular matrise gis n-te rekkefølge:

hvor Δ = det EN ≠ 0.

Algebraisk elementkomplement matriser n-te orden MEN determinanten til matrisen ( n–1)-te rekkefølge oppnådd ved å slette Jeg-te linje og j-th kolonne av matrisen MEN:

La oss lage en såkalt vedlagte matrise:

hvor er de algebraiske komplementene til de tilsvarende elementene i matrisen MEN.
Legg merke til at de algebraiske komplementene til elementene i radene i matrisen MEN er plassert i de tilsvarende kolonnene i matrisen Ã , det vil si at matrisen transponeres samtidig.
Deling av alle matriseelementer Ã på Δ - verdien av determinanten til matrisen MEN, får vi den inverse matrisen som et resultat:

Vi legger merke til en rekke spesielle egenskaper til den inverse matrisen:
1) for en gitt matrise MEN sin inverse matrise er den eneste;
2) hvis det er en invers matrise, da høyre revers og venstre revers matriser faller sammen med den;
3) en spesiell (degenerert) kvadratisk matrise har ikke en invers matrise.

Hovedegenskapene til den inverse matrisen:
1) determinanten til den inverse matrisen og determinanten til den opprinnelige matrisen er resiproke;
2) den inverse matrisen til produktet av kvadratiske matriser er lik produktet av de inverse matrisene av faktorer, tatt i omvendt rekkefølge:

3) den transponerte inverse matrisen er lik den inverse matrisen fra den gitte transponerte matrisen:

EKSEMPEL Beregn matrisen invers av den gitte.

invers matrise er en matrise A -1, når multiplisert med den gitte startmatrisen EN gir identitetsmatrisen E:

AA −1 = A −1 A =E.

Invers matrisemetode.

Invers matrisemetode- dette er en av de vanligste metodene for å løse matriser og er vant til løsninger av systemer med lineære algebraiske ligninger(SLAE) i tilfeller hvor antall ukjente tilsvarer antall ligninger.

La det være et system n lineære ligninger med n ukjent:

Et slikt system kan skrives som en matriseligning A*X=B,

hvor
- systemmatrise,

- kolonne med ukjente,

- kolonne med frie koeffisienter.

Fra den utledede matriseligningen uttrykker vi X ved å multiplisere begge sider av matriseligningen til venstre med A-1, resulterer i:

A -1 * A * X = A -1 * B

Vet det A-1*A=E, deretter E*X=A-1*B eller X=A-1*B.

Det neste trinnet er å bestemme den inverse matrisen A-1 og multiplisert med kolonnen med frie termer B.

Invers matrise til matrise EN eksisterer bare når det A≠ 0 . I lys av dette, når du løser SLAE ved invers matrisemetoden, er det første trinnet å finne det A. Hvis en det A≠ 0 , så har systemet bare én løsning, som kan oppnås ved invers matrisemetoden, if det A = 0, så et slikt system invers matrisemetode er ikke løst.

Invers matriseløsning.

Rekkefølge av handlinger for invers matriseløsninger:

Få matrisedeterminanten EN. Hvis determinanten er større enn null, løser vi den inverse matrisen videre, hvis den er lik null, kan den inverse matrisen ikke finnes her.
Finne den transponerte matrisen PÅ.
Vi ser etter algebraiske komplementer, hvoretter vi erstatter alle elementene i matrisen med deres algebraiske komplementer.
Vi samler den inverse matrisen fra algebraiske tillegg: vi deler alle elementene i den resulterende matrisen med determinanten til den opprinnelig gitte matrisen. Den endelige matrisen vil være den ønskede inverse matrisen i forhold til den opprinnelige.

Algoritmen nedenfor invers matriseløsninger i hovedsak det samme som ovenfor, forskjellen er bare i noen få trinn: først og fremst bestemmer vi de algebraiske tilleggene, og etter det beregner vi unionsmatrisen C.

Finn ut om den gitte matrisen er kvadratisk. Ved et negativt svar blir det klart at det ikke kan være en invers matrise for det.
Finn ut om den gitte matrisen er kvadratisk. Ved et negativt svar blir det klart at det ikke kan være en invers matrise for det.
Vi beregner algebraiske addisjoner.
Vi komponerer den allierte (gjensidige, vedlagte) matrisen C.
Vi komponerer en invers matrise fra algebraiske addisjoner: alle elementer i den adjoint matrisen C dividere med determinanten til den opprinnelige matrisen. Den resulterende matrisen vil være den ønskede inverse matrisen i forhold til den gitte.
Vi sjekker arbeidet som er utført: vi multipliserer de innledende og resulterende matrisene, resultatet skal være identitetsmatrisen.

Dette gjøres best med en vedlagt matrise.

Teorem: Hvis vi tilordner en identitetsmatrise av samme orden til en kvadratisk matrise på høyre side og transformerer startmatrisen til venstre til en enhetsmatrise ved bruk av elementære transformasjoner over rader, så vil den som oppnås på høyre side være invers til den første.

Et eksempel på å finne den inverse matrisen.

Trening. For matrise finn det inverse ved adjoint matrisemetoden.

Beslutning. Vi legger til den gitte matrisen MEN til høyre, identitetsmatrisen av 2. orden:

Trekk 2. fra 1. linje:

Trekk de 2 første fra den andre linjen:

Matrisen $A^(-1)$ kalles den inverse av kvadratmatrisen $A$ hvis $A^(-1)\cdot A=A\cdot A^(-1)=E$, hvor $E $ er identitetsmatrisen, hvis rekkefølge er lik rekkefølgen til matrisen $A$.

En ikke-singular matrise er en matrise hvis determinant ikke er lik null. Følgelig er en degenerert matrise en hvis determinant er lik null.

Den inverse matrisen $A^(-1)$ eksisterer hvis og bare hvis matrisen $A$ er ikke-singular. Hvis den inverse matrisen $A^(-1)$ eksisterer, er den unik.

Det er flere måter å finne inversen til en matrise på, og vi skal se på to av dem. Denne siden vil diskutere adjoint matrise-metoden, som regnes som standard i de fleste høyere matematikkkurs. Den andre måten å finne den inverse matrisen (metoden for elementære transformasjoner), som innebærer bruk av Gauss-metoden eller Gauss-Jordan-metoden, vurderes i den andre delen.

Adjoint (union) matrisemetode

La matrisen $A_(n\ ganger n)$ gis. For å finne den inverse matrisen $A^(-1)$, kreves det tre trinn:

Finn determinanten til matrisen $A$ og sørg for at $\Delta A\neq 0$, dvs. at matrisen A er ikke degenerert.
Komponer algebraiske komplementer $A_(ij)$ av hvert element i matrisen $A$ og skriv ned matrisen $A_(n\ ganger n)^(*)=\left(A_(ij) \right)$ fra det funnet algebraiske komplementer.
Skriv den inverse matrisen ved å ta hensyn til formelen $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Matrisen $(A^(*))^T$ blir ofte referert til som den tilstøtende (gjensidige, allierte) matrisen til $A$.

Hvis avgjørelsen tas manuelt, er den første metoden bare god for matriser med relativt små bestillinger: andre (), tredje (), fjerde (). For å finne den inverse matrisen for en høyere ordens matrise, brukes andre metoder. For eksempel Gauss-metoden, som er omtalt i andre del.

Eksempel #1

Finn matrise invers til matrise $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Siden alle elementene i den fjerde kolonnen er lik null, er $\Delta A=0$ (dvs. matrisen $A$ er degenerert). Siden $\Delta A=0$, er det ingen matrise invers til $A$.

Svar: matrise $A^(-1)$ eksisterer ikke.

Eksempel #2

Finn matrisen invers til matrisen $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Kjør en sjekk.

Vi bruker adjoint matrise-metoden. La oss først finne determinanten til den gitte matrisen $A$:

$$ \Delta A=\venstre| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Siden $\Delta A \neq 0$ eksisterer den inverse matrisen, så vi fortsetter løsningen. Finne algebraiske komplementer

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(justert)

Komponer en matrise av algebraiske komplementer: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transponer den resulterende matrisen: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (den resulterende matrisen kalles ofte adjoint- eller unionsmatrisen til matrisen $A$). Ved å bruke formelen $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, har vi:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

Så den inverse matrisen er funnet: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array) \right) $. For å sjekke sannheten til resultatet er det nok å sjekke sannheten til en av likhetene: $A^(-1)\cdot A=E$ eller $A\cdot A^(-1)=E$. La oss sjekke likheten $A^(-1)\cdot A=E$. For å jobbe mindre med brøker, vil vi erstatte matrisen $A^(-1)$ ikke i formen $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ men som $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \ end(array)\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( array)\right)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array) )\right) =E $$

Svar: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Eksempel #3

Finn inversen til matrisen $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$. Kjør en sjekk.

La oss starte med å beregne determinanten til matrisen $A$. Så determinanten for matrisen $A$ er:

$$ \Delta A=\venstre| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

Siden $\Delta A\neq 0$ eksisterer den inverse matrisen, så vi fortsetter løsningen. Vi finner de algebraiske komplementene til hvert element i den gitte matrisen:

Vi komponerer en matrise med algebraiske tillegg og transponerer den:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

Ved å bruke formelen $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, får vi:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

Så $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. For å sjekke sannheten til resultatet er det nok å sjekke sannheten til en av likhetene: $A^(-1)\cdot A=E$ eller $A\cdot A^(-1)=E$. La oss sjekke likheten $A\cdot A^(-1)=E$. For å jobbe mindre med brøker, vil vi erstatte matrisen $A^(-1)$ ikke i formen $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, men som $\frac(1)(26)\ cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(array) \right) =\frac(1)(26)\cdot\left(\begin(array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (array) \right) =\left(\begin(array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

Kontrollen ble bestått, den inverse matrisen $A^(-1)$ ble funnet riktig.

Svar: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Eksempel #4

Finn matriseinvers av $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

For en matrise av fjerde orden er det noe vanskelig å finne den inverse matrisen ved å bruke algebraiske addisjoner. Slike eksempler finnes imidlertid i kontrollarbeidene.

For å finne den inverse matrisen, må du først beregne determinanten til matrisen $A$. Den beste måten å gjøre dette på i denne situasjonen er å utvide determinanten i en rad (kolonne). Vi velger en hvilken som helst rad eller kolonne og finner det algebraiske komplementet til hvert element i den valgte raden eller kolonnen.

For eksempel, for den første raden får vi:

$$ A_(11)=\venstre|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\venstre|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\venstre|\begin(array)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\venstre|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

Determinanten til matrisen $A$ beregnes med følgende formel:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14) )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(justert) $$

Algebraisk komplementmatrise: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36 \\ 473 & -250 & -463 & -96\end(array)\right)$.

Vedlagt matrise: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Invers matrise:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Kontroll, om ønskelig, kan gjøres på samme måte som i de foregående eksemplene.

Svar: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(array) \right) $.

I den andre delen vil en annen måte å finne den inverse matrisen vurderes på, som innebærer bruk av transformasjoner av Gauss-metoden eller Gauss-Jordan-metoden.

ALGEBRAISK TILLEGG OG MINDRE

La oss ha en tredjeordens determinant: .

Liten tilsvarende dette elementet aij tredjeordens determinant kalles andreordensdeterminanten hentet fra den gitte ved å slette raden og kolonnen i skjæringspunktet det gitte elementet står i, dvs. Jeg-te linje og j-te kolonne. Mindreårige som tilsvarer et gitt element aij vi vil betegne M ij.

for eksempel, liten M12 tilsvarende elementet en 12, vil det være en determinant 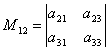, som oppnås ved å slette 1. rad og 2. kolonne fra den gitte determinanten.

Dermed viser formelen som bestemmer tredjeordens determinanten at denne determinanten er lik summen av produktene til elementene i 1. rad og deres tilsvarende mindreårige; mens moll tilsvarer elementet en 12, er tatt med "–"-tegnet, dvs. kan skrives det

(1)

På samme måte kan man introdusere definisjoner av mindreårige for determinanter av andre orden og høyere orden.

La oss introdusere et konsept til.

Algebraisk tillegg element aij determinant kalles dens minor M ij multiplisert med (–1) i+j .

Algebraisk elementtilsetning aij angitt En ij.

Fra definisjonen får vi at sammenhengen mellom det algebraiske komplementet til et element og dets minor er uttrykt ved likheten En ij= (–1) i+j M ij .

For eksempel,

Eksempel. Gitt en determinant. Å finne A 13 , A 21 , A 32.

Det er lett å se at ved å bruke algebraiske tillegg av elementer, kan formel (1) skrives som:

På samme måte som denne formelen kan man oppnå dekomponeringen av determinanten over elementene i en hvilken som helst rad eller kolonne.

For eksempel kan dekomponeringen av determinanten over elementene i den andre raden oppnås som følger. I henhold til egenskap 2 til determinanten har vi:

La oss utvide den oppnådde determinanten med elementene i den første raden.

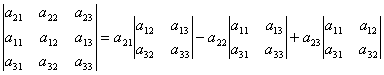(2)

Herfra fordi andreordens determinantene i formel (2) er minorene til elementene en 21, en 22, en 23. Dermed, dvs. vi har fått utvidelsen av determinanten med elementene i den andre raden.

På samme måte kan man oppnå dekomponering av determinanten over elementene i den tredje raden. Ved å bruke egenskap 1 til determinanter (ved transposisjon) kan man vise at lignende utvidelser også er gyldige for utvidelser når det gjelder kolonneelementer.

Dermed er følgende teorem sann.

Teorem (om utvidelse av determinanten i en gitt rad eller kolonne). Determinanten er lik summen av produktene til elementene i noen av radene (eller kolonnene) og deres algebraiske komplementer.

Alt det ovennevnte er sant for determinanter av høyere orden.

Eksempler.

INVERS MATRIKSE

Konseptet med en invers matrise er kun introdusert for kvadratiske matriser.

Hvis en EN er en kvadratisk matrise, da omvendt for det er en matrise en matrise betegnet A-1 og tilfredsstiller betingelsen. (Denne definisjonen er introdusert i analogi med multiplikasjon av tall)